1.3.3. Понятие эталонной 6, случайной величины 

Выберем интервал чисел от 0 до 1. Представим себе, что мы имеем некоторый генератор выработки случайных чисел х по равномерному распределению в интервале [0, 1], т.е. для области 0 < х < 1, функция распределения равна , а плотность вероятности реализации случайного числа соответственно равна единице .

Рассмотрим случайный эксперимент, при проведении которого реализуется равномерное распределение случайных чисел в некотором интервале. В результате опыта мы получаем некоторое число , которое может быть представлено в виде

, например, в результате розыгрыша упало число

 = 0.4603721….,

Реализованные в результате розыгрыша числа  , лежащие в интервале [0, 1], в дальнейшем будем называть эталонными случайными числами, а цифры _i, входящие в случайные числа, называть десятичными, случайными цифрами, в отличие от случайных цифр, в другой системе исчисления. Причем каждая цифра является независимой от других цифр.

При решении реальных задач в случайной величине  количество случайных цифр после запятой выбирают конечным, т.е.

. (1.31)

Можно сказать, что при вероятностно-имитационном компьютерном моделировании реальных явлений, эталонная или стандартная случайная величина  является базовой для получения случайных величин в другом диапазоне (интервале) и для других распределений плотности вероятности.

1.3.4. Преобразование случайных величин 7

В методе Монте-Карло часто стоит задача преобразования одной случайной величины в другую.

Рассмотрим функцию распределения непрерывной случайной величины, которая по определению имеет вид

, (1.32)

где функция F(x) меняется от 0 до 1.

Приведем без доказательства одну из теорем преобразования случайной величины.

Случайная величина, удовлетворяющая уравнению

(1.33)

имеет плотность вероятности f(x).

Эта теорема позволяет получать формулы преобразования одной случайной величины в другую для различных законов распределения.

Пример 1. Например, рассмотрим случайный эксперимент, плотность вероятности которого подчиняется равномерному распределению

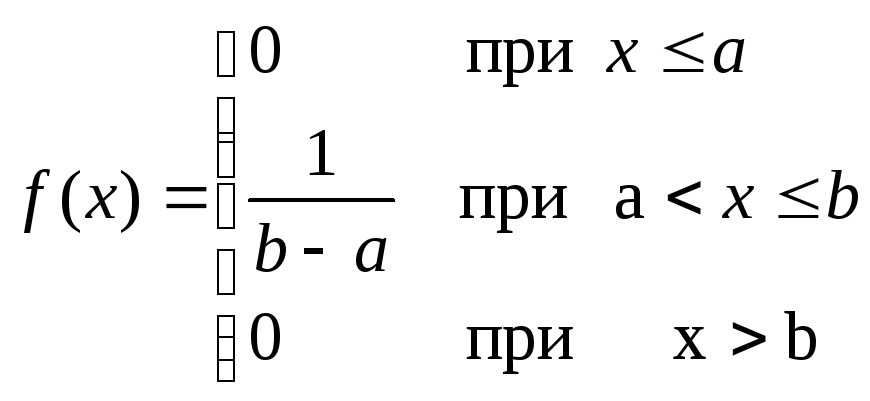
здесь случайная величина х лежит в промежутке [а, b].

Применим формулу (1.33),

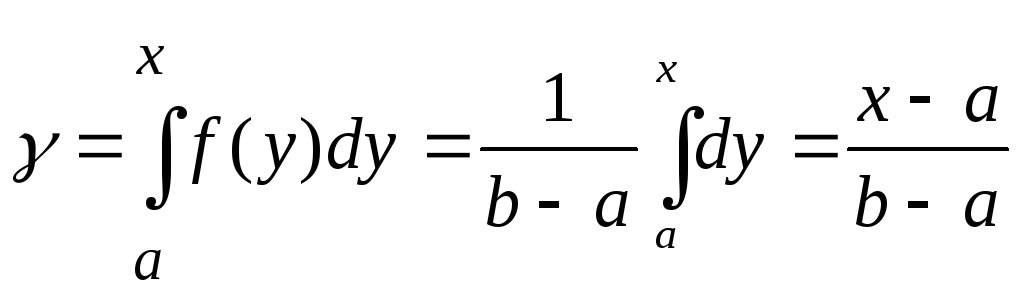, (1.34)

Откуда получаем формулу преобразования для равномерного распределения

х = а + (b — а)  , (1.35)

т.е. для определения случайных величин в этом интервале мы обращаемся к последовательности случайных чисел, равномерно распределенных на отрезке [0, 1], т.е. к эталонной случайной величине , а случайную величину х в интервале [а, b] получаем по формуле преобразования (1.35).

Пример 2. Рассмотрим теперь экспоненциальное распределение

. (1.36)

Так как

, (1.37)

то для расчета экспоненциальной случайной величины х имеем следующую формулу

. (1.38)

Пример 3. Для получения гауссовской (нормированной) случайной величины х (а=0, =1) мы должны решить уравнение и найти х

.

Решить это уравнение достаточно трудно, поэтому используют другие методы преобразования.

1). Один из способов преобразования случайной величины для получения гауссовского распределения – это использование суммы n независимых, равномерно распределенных величин типа

, (1.39)

согласно центральной предельной теореме при n   имеем, что

, (1.40)

т.е. для больших n можно использовать эту асимптотику. Опыт показывает, что при значении n=12 можно использовать формулу

, (1.41)

где _i - равномерно распределенные случайные числа от 0 до 1. Для получения одного значения  в этом случае используются 12 значений .

Иногда для определения случайной величины для гауссовского распределения используют следующую формулу

. (1.42)

Здесь добавлена поправка, которая ускоряет сходимость распределения к нормальному.

2). Другой способ преобразования эталонного случайного числа в гауссовское – это использование алгоритма Малера, который достаточно эффективен и дает сразу два значения . (1.43)

Если нужно только одно значение, то можно выбрать одну из этих формул. Если случайная величина х нормирована, т.е a=0 и =1, то для получения гауссовской случайной величины у с математическим ожиданием a и дисперсией  используют преобразование

. (1.44)

Пример 4. Моделирование равновероятного направления в трехмерном пространстве (равнораспределенная на поверхности сферы).

Элемент вероятности направления в трехмерном пространстве в декартовой и сферической системе координат для единичного вектора имеет вид

.

Здесь проекции единичного вектора. Рассмотрим несколько алгоритмов получения случайных чисел для проекций единичного вектора.

1. . Берутся два случайные числа ₁ и ₂ и по алгоритму

, (1.45)

определяются три случайных числа е_x, е_у, е_z , которые являются проекциями единичного вектора.

2. . Берутся три случайные числа ₁, ₂ и ₃ и вычисляется величина

, (1.46)

Если d<1, p= / 6, то вычисляются

. (1.47)