2.2. Вычисление интегралов способом среднего

Пусть случайная величина y является функцией от случайной величины х. По определению среднего

(2.17)

В теории вероятностей доказывается, что для случайной величины с плотностью распределения всегда можно найти такую случайную величину с плотностью распределения , так что

или . (2.18)

Эта операция иногда называется преобразованием случайной величины. Преобразование случайной величины является узловым моментом в теории статистических испытаний (Монте-Карло). Обычно в качестве исходной (базовой) случайной величины выбираются случайные цифры и из них строятся случайные числа в интервале от 0 до 1. Случайные цифры можно генерировать с помощью ЭВМ или пользоваться таблицей случайных чисел (см.приложение). Например, 8631 6918 4168 8652 6712 2039 и т.д. Построим из них числа от 0 до 1: 0,8631; 0,6918; 0,4168; 0, 8652; 0,6712; 0, 2039 и т.д.

Пусть у нас имеется случайная величина в интервале от 0 до 1. Если нам нужно перейти к другой случайной величине , то формула перехода , согласно определению непрерывной случайной величины, имеет вид:

(2.19)

Здесь - нами взятая произвольная плотность распределения. Следует отметить, что удачный выбор плотности распределения вероятности во многом определяет затраты и точность вычислений в методе Монте-Карло.

Технология вычисления интеграла способом среднего

Рассмотрим вычисление определенного интеграла

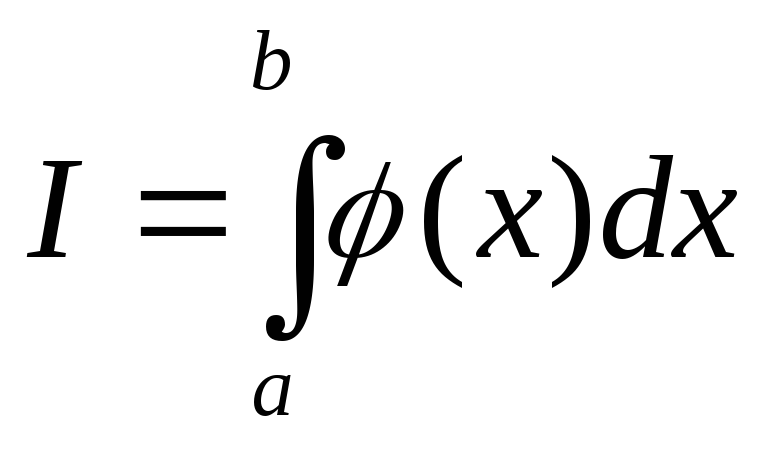. (2.20)

для этого берем случайную величину , распределенную в интервале от а до b с плотностью распределения , и построим другую функцию в виде

.

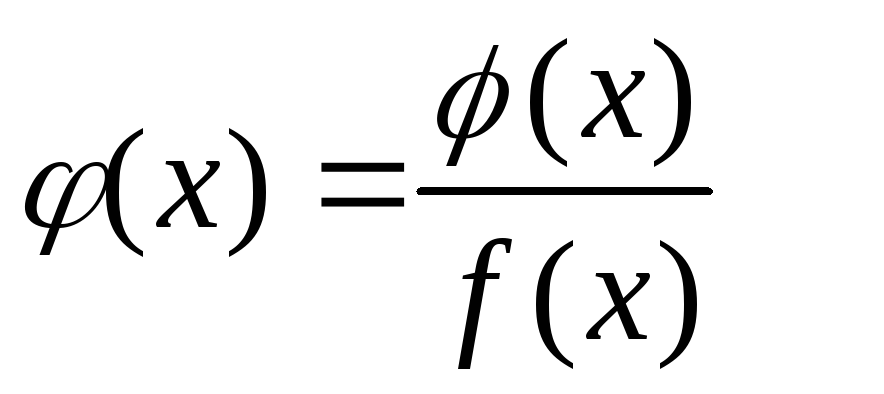Тогда

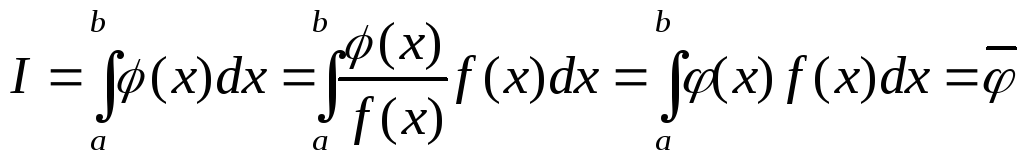. (2.21)

Введем обозначение , тогда случайная величина у определится как

.

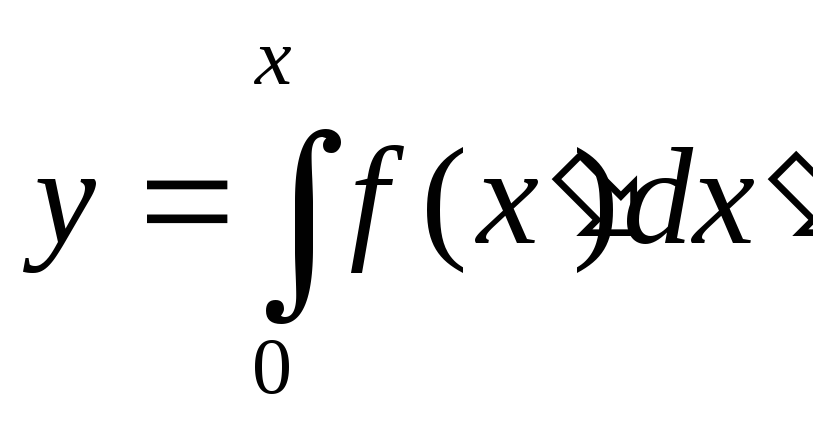Вычисляя этот интеграл, получим зависимость у = у ( х ), откуда выражаем х и подставляем в функцию (х(у)).

Тогда интеграл (2.21) примет вид

.

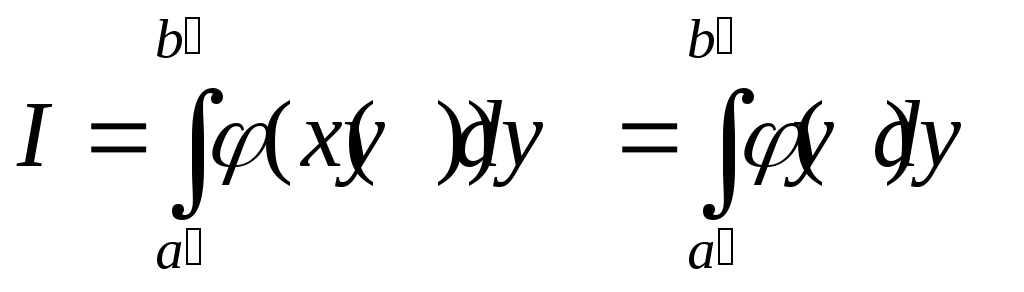Отметим, что если случайная величина х лежит в интервале [a,b], то для случайной величины у, пределы интервалов также необходимо изменить, тогда наш искомый интеграл определится как

.

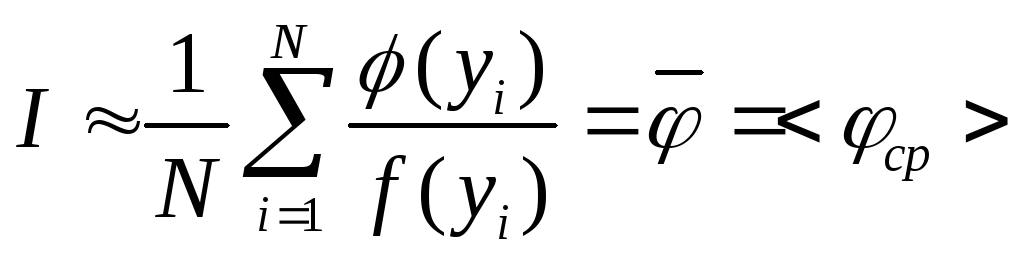Пример. В качестве иллюстрации вычислим следующий интеграл методом статистических испытаний

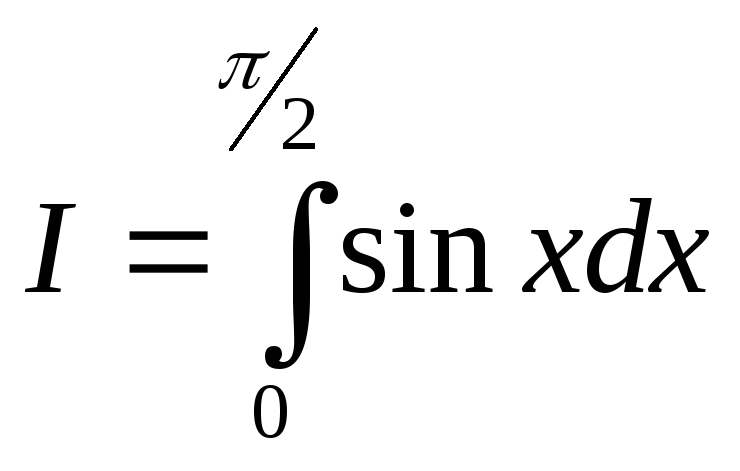, (2.22)

зная, что точное значение этого интеграла I = 1.

1. Случай равномерного распределения. Берем случайную величину , принимающую значения в интервале от 0 до /2 и подчиняющуюся закону равномерного распределения 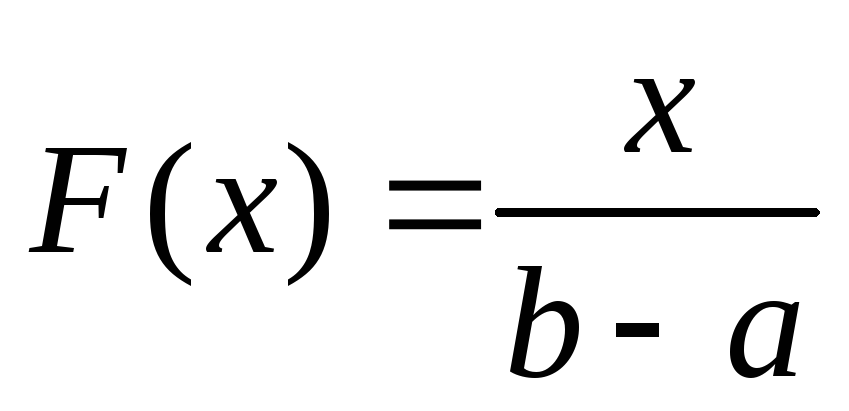(а= 0 и b = /2).

Плотность распределения вероятности

.

Для перехода от случайной величины в интервале [0, /2] к случайной величине выполним преобразование по формуле (2.19)

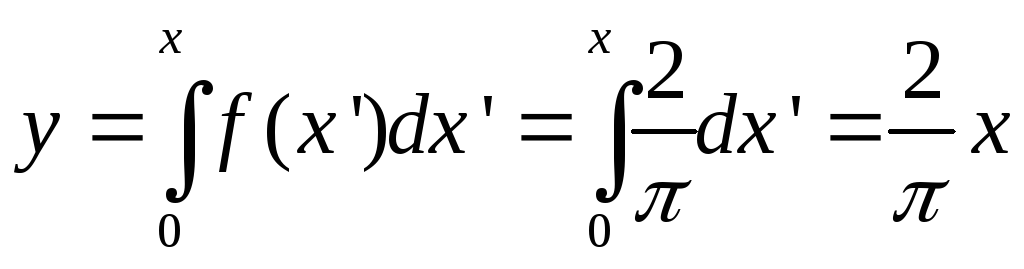. (2.23)

Плотность распределения f(y) случайной величины y имеет вид

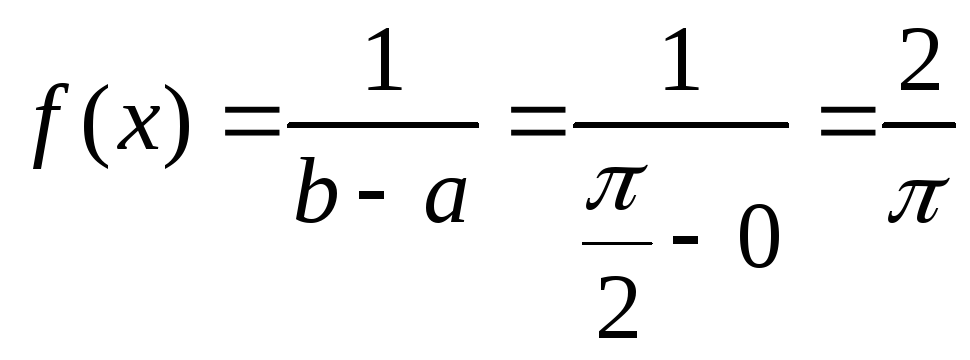. (2.24)

Вычисляемый интеграл можем представить как

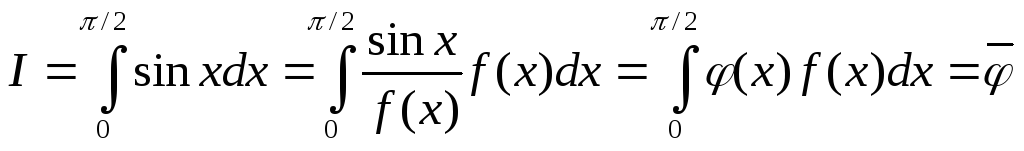. (2.25)

Вычисление интеграла (2.22) проведем методом Монте-Карло.

Из формулы (2.23) найдем х

. (2.26)

т.к. интервал изменения х равен [0, /2], то интервал изменения у будет равен [0, 1]. Теперь, используя формулу 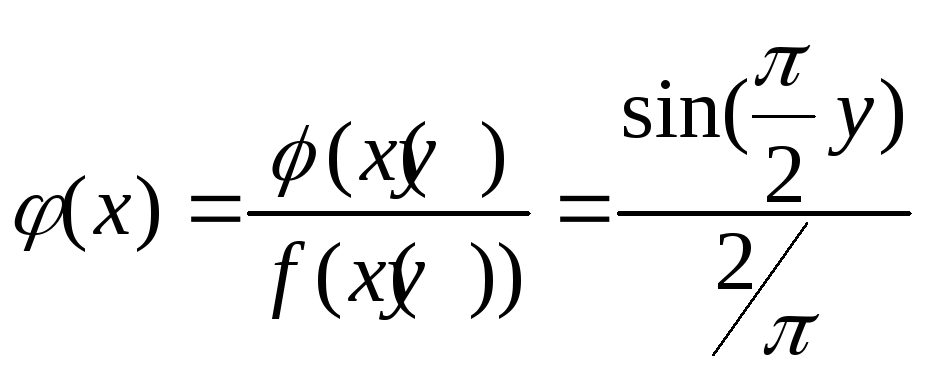, запишем интеграл в виде

.

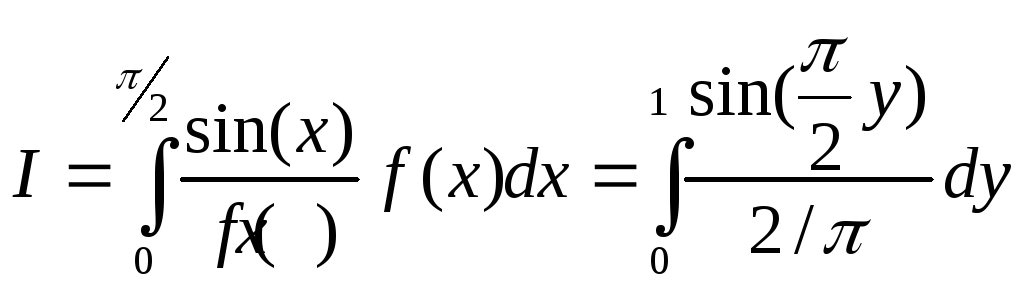Переходя от интеграла к сумме, получим алгоритм определения значения интеграла (2.26) .

,

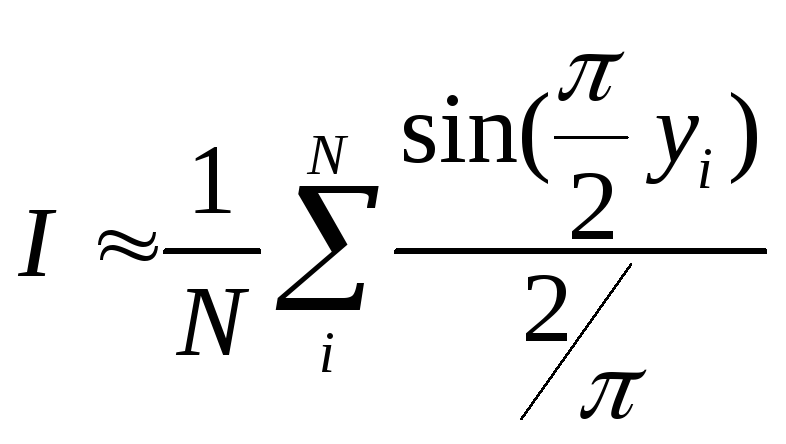, (2.27)

здесь - случайная величина, лежащая в интервале [0, 1], i =1, 2, 3, …..N. Для наглядности приведем результаты вычислений в виде таблицы.

	1	2	3	4	5	6	7	8	9	10
уi	0,8631	0,6918	0,4168	0,8652	0,6712	0,2039	0,0339	0.4216	0.4717	0.6615
 yi/2	1,359	1,087	0.6446	1.359	1.054	0.3202	0.053	0.662	0.741	1.039
Sin( yi/2)	0,978	0.885	0.6088	0.9777	0.8694	0.3148	0.053	0.6147	0.675	0.862
 Sin (yi) /2	1.536	1.391	0.9564	1.536	1.366	0.4945	0.085	0.96	1.06	1.35

Интеграл I определяется по алгоритму (2.27). При N=10 получается I = 1.06.

2. Случай неравномерного распределения. Выберем для простоты плотность распределения случайной величины х вида

. (2.28)

Найдем постоянную А из условия нормировки 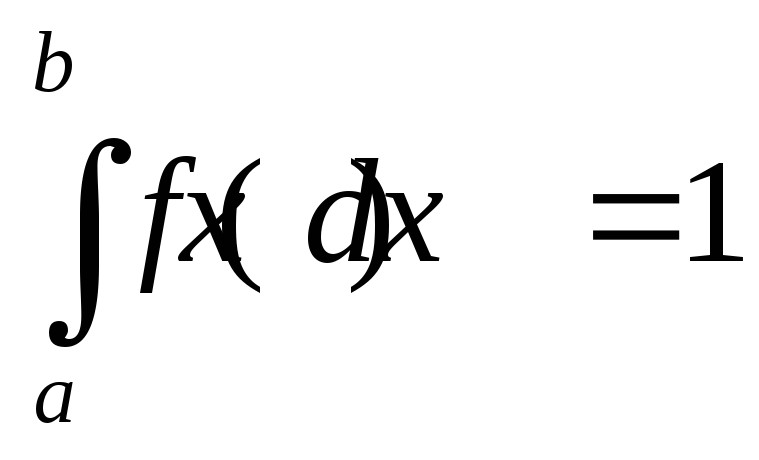для нашей задачи .

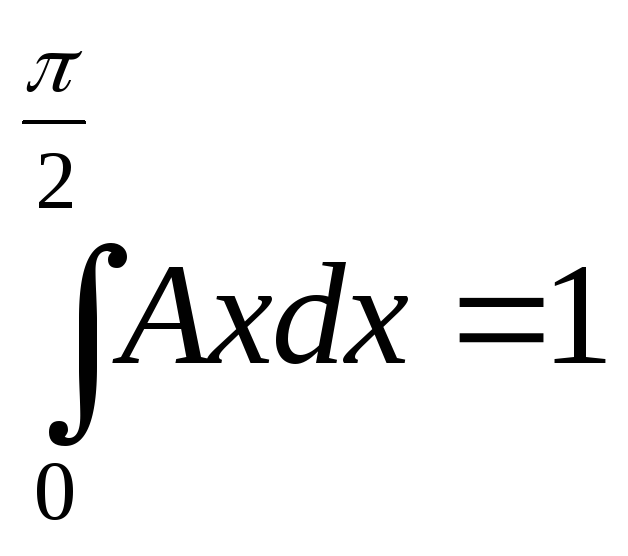Отсюда .

Следовательно, плотность распределения случайной величины имеет вид

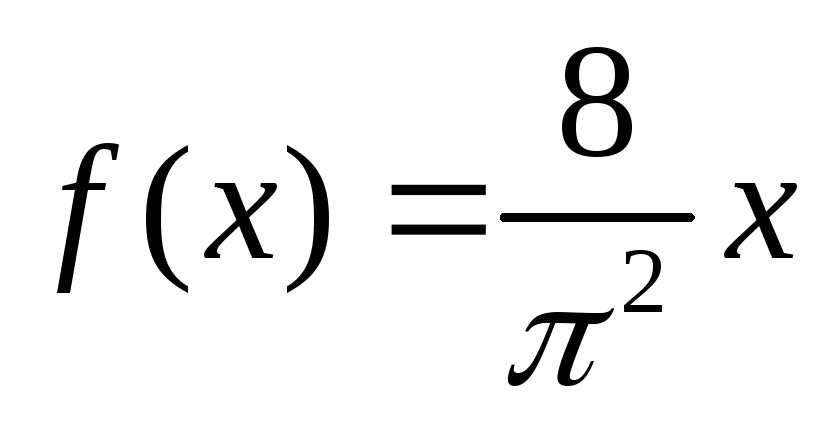. (2.29)

Проведем преобразование случайной величины. Для этого перейдем от случайной величины , распределенной в интервале [0,/2] , к случайной величине у по соотношению

. (2.30)

Подставляя пределы интегрирования по , из формулы (2.30) найдем пределы интегрирования по величине у, она лежит в пределах [0, 1]. Используя обратную функцию и плотность распределения

,

найдем функцию , т.е.

.

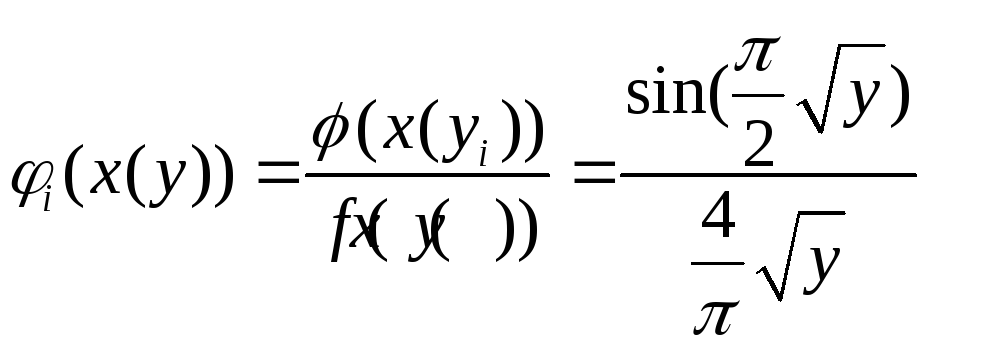Тогда интеграл (2.25) примет вид

.

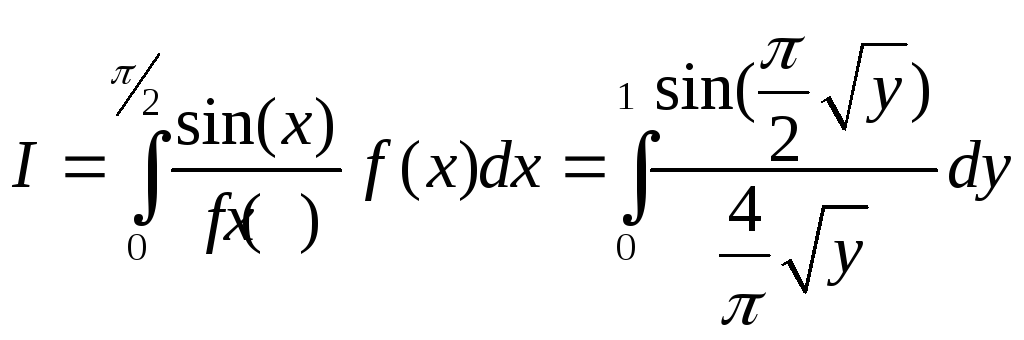Переходя от интеграла к сумме, получаем формулу вычисления интеграла (2.22)

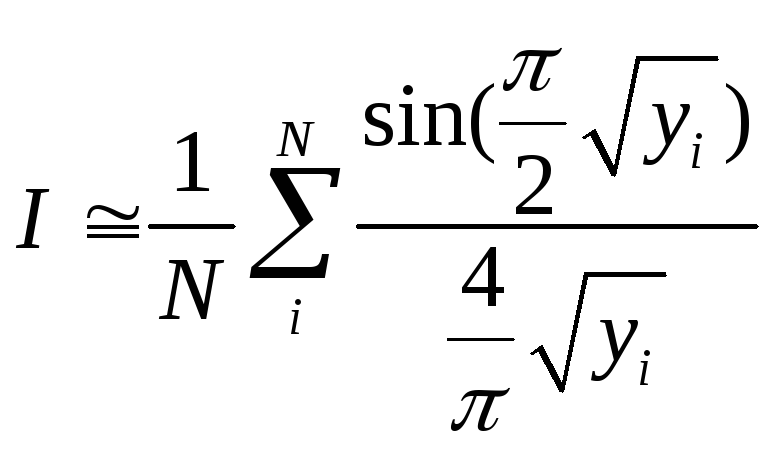. (2.31)

Здесь у_i случайная величина, лежащая в интервале [0, 1].

Интересно сравнение результатов формул (2.27) и (2.31) при одном и том же N.

Таким образом, метод Монте-Карло может быть реализован в виде разных алгоритмов с различной эффективностью.

Для сравнения эффективности вводят понятие о трудоемкости алгоритма, которая определяется как произведение времени расчета одного значения х на дисперсию случайной величины.

.

Задания на моделирование:

Вычислить методом статистических испытаний интегралы ошибок erf(у):

, (2.32)

для с интервалом 0, 1 ().

В качестве плотности распределениявыбрать:

1. Линейное распределение .

2. Экспоненциальное распределение .

Постоянные А₁ и А₂ найти из условия нормировки. Вычисленные значения сравнить с табличными данными и оценить ошибки вычислений в каждом случае. Число испытаний N рекомендуется брать не меньше 100.