1.3. Генераторы, алгоритмы получения и преобразования случайных чисел

Суть компьютерного моделирования методом Монте-Карло заключается в следующем: случайному эксперименту реального явления или процесса или описывающим его дифференциальным уравнениям сопоставляется аналогичный им (иногда совершенно непохожий) вероятностный процесс, который моделирует это явление, т.е. создается вероятностная модель исследуемого явления. На вероятностной модели проводятся исследования, отрабатываются возможные решения, чаще всего на компьютере, которые затем переносятся на реальный процесс или явление.

Однако для проведения испытаний в вероятностной модели необходимы генераторы случайных чисел. Где взять эти генераторы в реалии, а если задача решается на компьютере, как создать генераторы истинно случайных чисел для ЭВМ и как использовать их для решения задач в методе Монте-Карло?

Таким образом, для решения вероятностной модели стоит задача получения случайных чисел.

1.3.1. Получение случайных чисел с помощью случайного эксперимента

Генераторов получения случайных чисел с помощью опытов можно придумать бесконечное множество. Приведем примеры.

1. Самый простой генератор – это однородный кубик с нанесенными на него числами от 0 до 5 (игральная кость). Проводя N опытов выброса кости, мы получаем случайные цифры в шестеричной системе исчисления. Из шестеричной системы по алгоритмам преобразования можно получить случайные цифры в десятеричной системе исчисления.

2. Следующий простой генератор – это монета. Если проведем N опытов выброса монеты, то мы получаем случайные события «орел» или «решку». Обозначим их соответственно нулем или единицей, иначе говоря, цифрами в двоичной системе исчисления, тогда процедура бросания монеты является генератором двоичных цифр.

3. Рулетка в игровых домах и клубах представляет собой тарелкообразную форму, при бросании шарика по краям рулетки шарик, совершив несколько оборотов, падает в ячейки, находящиеся на краях дна рулетки. Ячейки соответственно пронумерованы. Попадание шарика в определенную ячейку – событие чисто случайное. Проводя N опытов, мы получаем последовательность случайных чисел.

4. Для реализации розыгрыша случайных чисел в различных видах лотереи и игральных автоматах используются специальные устройства (генераторы случайных чисел), которые выбрасывают эти случайных числа.

1.3.2. Алгоритмы получения псевдослучайных чисел 5

Проведем случайный эксперимент, в результате которого наблюдаем или получаем случайное число. Используя это случайное число, по какой-либо заданной формуле преобразуем его в другое случайное число, затем повторяем эту итерацию, тогда в конечном счете получаем ряд случайных чисел. Таким образом, полученные случайные числа называются псевдослучайными числами. Отметим, что при использовании формул для получения случайных чисел через какое-то число испытаний начинается повторение случайных чисел, т.е. псевдослучайные числа периодичны, иначе говоря, запас псевдослучайных чисел ограничен. Вопрос состоит только в том, каков период псевдослучайных чисел? Это зависит от выбранного алгоритма выработки псевдослучайных чисел.

Существует достаточное количество способов получения псевдослучайных чисел (см. в работах [5, 13, 22]). Рассмотрим без доказательства несколько способов получения псевдослучайных чисел.

1. Последовательность псевдослучайных чисел x_i, i= 1, 2, ..., можно полу­чить с помощью способа Лемера, или как говорят иногда методом вычетов. Алгоритм этого способа со­стоит в следующем [70]:

1. Первое случайное целое число r₁ выбирается между числами 0 и P, где число Р выбирается заранее.

2. Умножаем это случайное число на выбранный заранее постоянный множитель М.

3. К полученному произведению прибавляем некоторое выбран­ное заранее целое число К.

4. Результат первых трех шагов делим на Р и получившийся остаток выбираем в качестве следующего случайного числа. Формула представленного алгоритма имеет следующий вид: r_i+1 = (M r_i + К) mod P, i = 1, 2, ... Выбор различных значений М, К и Р дает различные периоды псевдослучайных последовательностей. Доказано, что лучше всего использовать целые числа. При К=0, а Р = 2 ^N наибольший период достигается при М=3+8*I или М = 5+8*I. В качестве начального числа r₁ желательно выбрать нечетное число. При достаточно больших числах М полученный ряд производит впечатление случайного ряда.

2. Для получения случайного числа можно использовать также другой алгоритм Лемера:

   1. Берем случайное число  и умножим его 10^2*k (₀ =*10^2*k )

   2. Возводим в квадрат ₀ ²

   3. Берем последние 2*k от ₀ ²

   4. Умножим на постоянное любое число С, получаем новое число ₁.

   5. Берем первые 2*k цифры от ₁, тогда получим число ₂.

   6. Берем первые 2*k от ₀ ²

   7. Умножим на постоянное любое число С, получаем новое число ₃.

   8. Берем последние 2*k цифры от ₃ , тогда получим число ₄.

   9. Случайное число  = (₁+₂)/(2*10^2*k).

3. Для генерирования эталонных псевдослучайных чисел можно также воспользоваться методом середины квадратов (метод Неймана), суть которого заключается в следующем: пусть 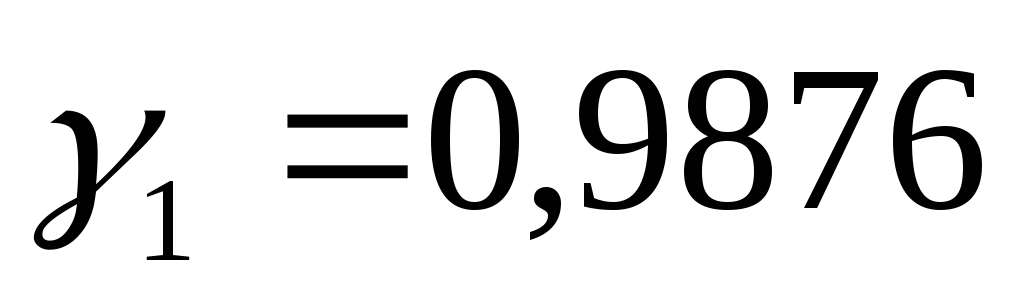тогда 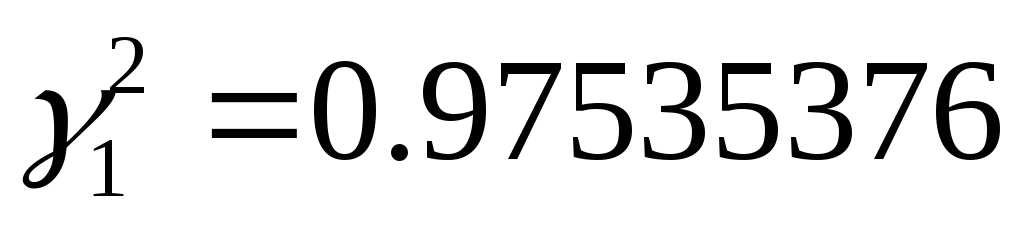, берем средние четыре цифры и составим 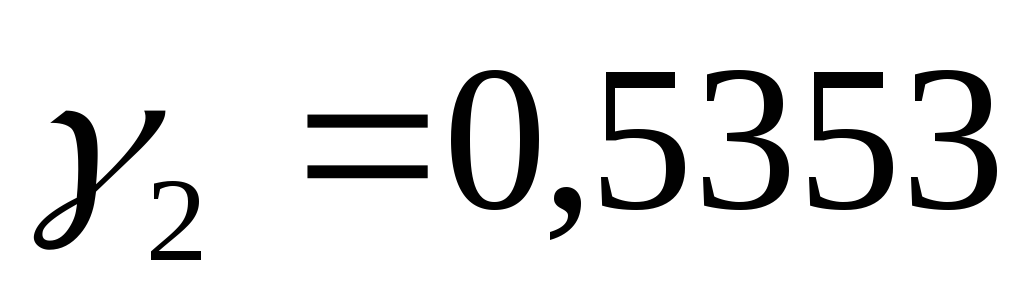, тогда 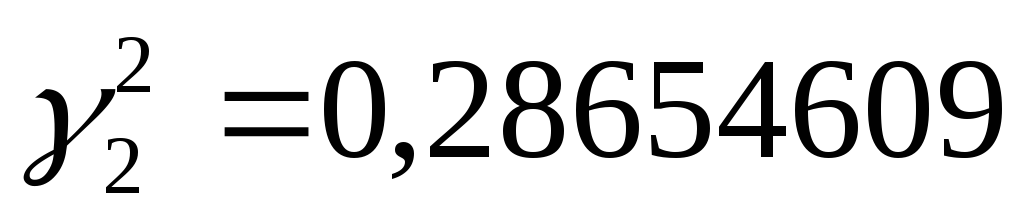Следовательно, 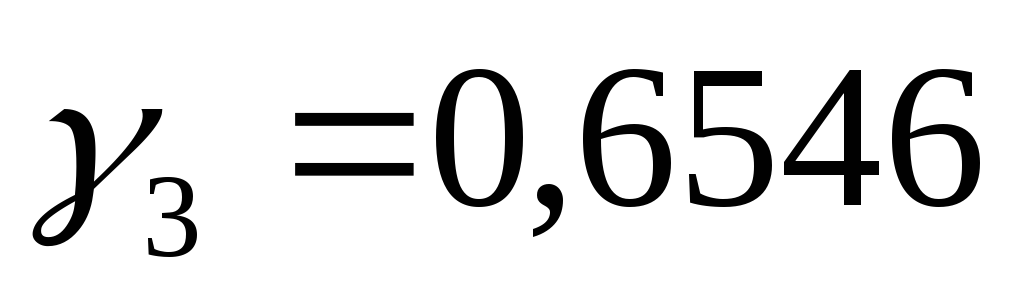и т.д., т.е. каждое последующее число образуется возведением предыдущего в квадрат и отбрасыванием цифр с обоих концов.

4. Следующий класс генераторов случайных чисел предложен А.Зейманом и Дж.Марсалиа. Генераторы этого типа основаны на использовании последовательности Фибоначчи. Пример такой последовательности {0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ….}. Рекурсивное описание последовательности Фибоначчи имеет вид 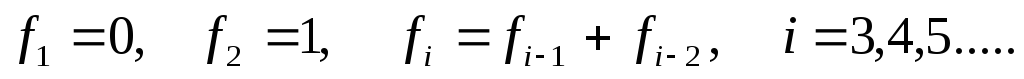, т.е. каждый последующий член равен сумме предыдущих. Если мы берем только последнюю цифру каждого числа в последовательности, то получим последовательность чисел {0, 1, 1, 2, 3, 5, 8, 3, 1, 4, 5, 9, 4 ….}. Если эта последовательность применяется для начального заполнения массива большой длины, то используя этот массив, можно создать генератор случайных чисел Фибоначчи с запаздыванием, где складываются не соседние, а удаленные числа.