1.2.2. Основные теоремы теории вероятностей 4

Приведем без доказательства основные теоремы теории вероятностей, которые понадобятся нам в дальнейшем.

Последовательность независимых экспериментов называется схемой Бернулли, если в каждом эксперименте возможно только 2 исхода, условно называемые успех и неуспех, при этом

Р { успеха } = p

P{ неуспеха} =q

Вероятность успехов в испытаниях Бернулли равна

(1.20)

Соответствующее распределение вероятностей на числах 0, 1,2,…, n обозначается - и называется биноминальным распределением с параметрами .

Пример. Пусть станок производит 100 изделий. Вероятность брака при производстве одного изделия равна . Какова вероятность того, что ровно 3 изделия окажутся бракованными?

По формуле (1.17) имеем

.

Часто на практике стоит задача об отыскании удобных асимптотических формул для вероятностей при и их сумм, эту задачу можно решить с помощью локальной и интегральной теорем Муавра – Лапласа.

Локальная теорема

Пусть , тогда справедливо представление :

, (1.21)

Иначе говоря, вероятность успехов в испытаниях Бернулли можно вычислить по данному представлению.

Пример. Пусть подбрасывается игральная кость 1000 раз. Оценим приближенно вероятность того, что в 1000 испытаниях шестерка выпадет 200 раз.

По локальной формуле Муавра-Лапласа имеем

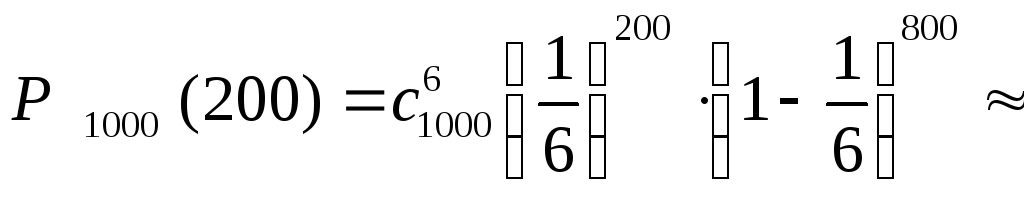
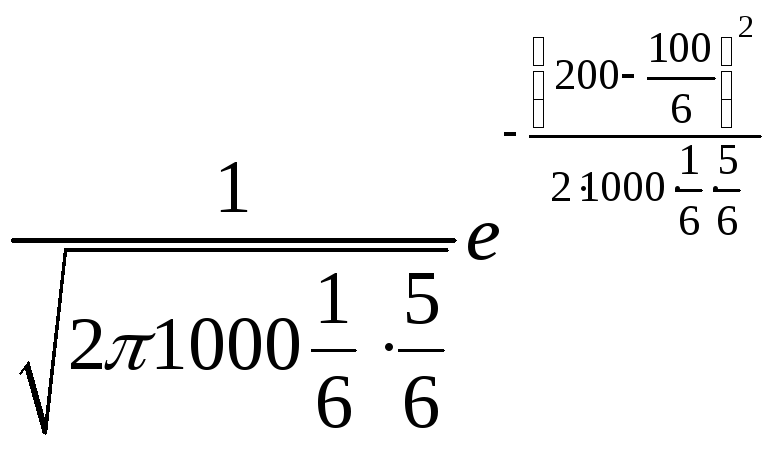
Отметим, что вычисления по точной формуле (1.21) являются непростой задачей.

Интегральная теорема

В различных задачах требуется находить вероятности вида: - т.е. вероятность того, что количество успехов X_n в испытаниях Бернулли в интервале [с, d], причем с< d.

Интегральная теорема гласит так

Для любого c < d интервала [с , d ] для схемы Бернулли имеет место

, (1.22)

для . Здесь функцию Ф можно посчитать по формуле

,

величина - количество успехов в испытаниях Бернулли.

Вероятностное распределение случайной величин по локальной теореме для каждого к в интервале [с, d] определяется как

, (1.23)

Здесь при определении вероятности можно использовать интегральную предельную теорему Муавра-Лапласа, согласно которой для больших n вероятность успехов в интервале [с, d] можно определить по предельной формуле (1.22). Для определения значений Ф можно использовать готовую таблицу (см. приложение).

Закон Больших Чисел

Это общий принцип, в силу которого суммарное действие большого количества случайных факторов при весьма общих условиях приводит к результату почти не зависящему от случая.

Первый результат в этом направлении получен Я.Бернулли (1713), его обобщение сделано П.Л.Чебышёвым (1867) и носит название теоремы Чебышева.

Пусть - последовательность независимых случайных величин и , тогда . Иначе говоря, если - арифметическая средняя, то , т.е. .

Теорему Чебышева можно сформулировать следующим образом:

Если Х₁, Х₂,…..Х_n – независимые случайные величины, имеющие одно и то же математическое ожидание а, дисперсии этих величин меньше некоторой константы и число случайных величин достаточно велико, то среднее арифметическое этих случайных величин примет значение, близкое к а.

Более строго, формулировка следующая

Какое бы ни было число  > 0 , имеет место

. (1.24)

Обычно число  выбирают достаточно малым, в этом случае Х_ср= а+.

Теорема Бернулли

Пусть мы имеем n независимых испытаний по реализации случайного события A, и в результате испытаний, событий A реализовалась всего n_A раз, тогда арифметическое среднее есть просто относительная частота события , т.е. и .

По Закону Больших Чисел имеем, что , т.е. относительная частота случайного события сближается с его вероятностью при возрастании числа наблюдений. Это следствие теоремы Чебышева и она носит название теоремы Бернулли.

Таким образом, теорему Бернулли можно сформулировать так:

Если проводится достаточно большое количество n независимых испытаний по определению события А, и вероятность р появления события А постоянна, то относительная частота появления события А окажется близкой к вероятности этого события.

Если более строго, то имеет место следующий предел

. (1.25)