42.Деревья. Свойства деревьев. Цикломатическое число. Остовные деревья графа. Алгоритм нахождения остовного дерева.

О: Связный неориентированный граф без циклов называется деревом.

О: Неориентированный граф все компоненты связности которого являются деревьями называется лесом.

Теорема 1: Для того чтобы связный граф был деревом необходимо и достаточно чтобы любые две его вершины были связаны единой цепью.

Теорема 2: дерево с n вершинами содержит n-1 ребро.

Теорема 3: n-число вершин, N-число ребер, V(E)=N-n+1 это цикломатическое число.

О: цикломатическим числом графа G называется число элементов его циклового базиса ( максимальное число независимых циклов)

Остовное дерево.

Остовным деревом G/ называется такое его подграф, который является деревом и содержит все вершины исходного графа.Алгоритм отыскания остовного дерева.

Остовное дерево может быть построено практически любым алгоритмом обхода графа, например поиском в глубину или поиском в ширину. Оно состоит из всех пар рёбер (u,v), таких, что алгоритм, просматривая вершину u обнаруживает в её списке смежности новую, необнаруженную ранее вершину v.

Остовные деревья, построенные при обходе графа алгоритмом Дейкстры, начиная из вершины s, обладают тем свойством, что кратчайший путь в графе из s до любой другой вершины — это (единственный) путь из s до этой вершины в построенном остовном дереве.

Если каждому ребру графа присвоен вес (длина, стоимость и т. п.), то нахождением оптимального остовного дерева, которое минимизирует сумму весов входящих в него рёбер, занимаются многочисленные алгоритмы нахождения минимального остовного дерева.

Минимальное остовное дерево (МОТ).

пусть каждому ребру неориентированного графа поставлено в соответствие число L(x,y)≥0

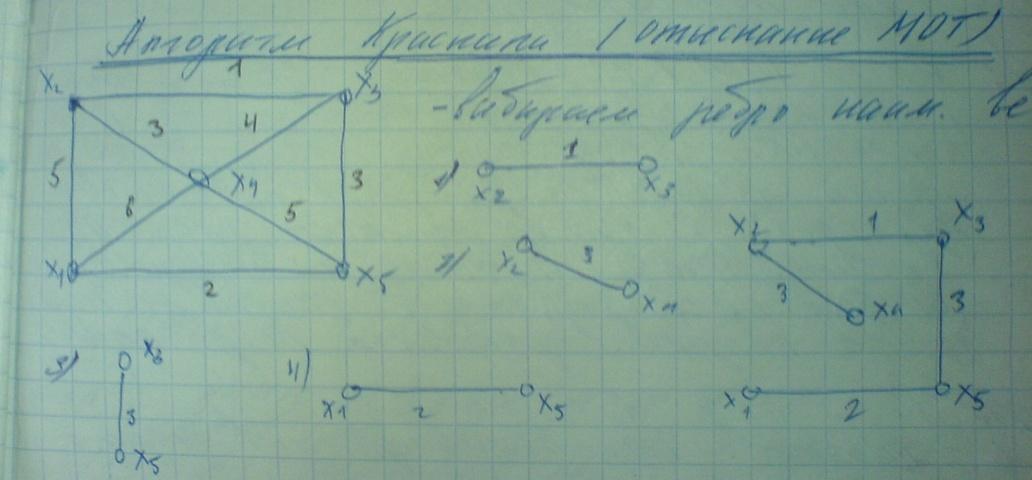
Алгоритм Краскала (мот)

Формулировка задачи. Дан взвешенный граф, в котором веса присвоены ребрам. Необходимо найти минимальное остовное дерево имеющую своим корнем одну из вершин графа.

 Идея алгоритма. Искомые ребра соединяют вершины. Поэтому возможны две стратегии построения. Можно идти от вершин и для каждой из них искать минимальное ребро (как это сделано в алгоритме Прима) а можно для каждого ребра выяснять можно ли его включить в строящееся дерево. Алгоритм Краскала предлагает делать это следующим образом. Во-первых, ребра графа пронумеровываем в порядке возрастания весов. Затем для каждого ребра начиная с первого проверяем соединяет или нет оно две несвязные вершины, если да, то его можно включить в остовное дерево. Ясно, что если мы имеем V вершин, то работа алгоритма начинается с V несвязных компонент графа (пока из графа все ребра исключаем). Для того, чтобы их связать необходимо найти V-1 ребро.

Другими словами, алгоритм организует процесс роста компонент связности в процессе которого он объединяются друг с другом до тех пор пока не останется одна являющаяся конечным результатом.

 Алгоритм

1)Создаем список ребер по возрастанию. 2)Создаем множество компонент связности каждая из которых содержит ровно одну вершину пока компонент связности больше чем одна. 3)Взять ребро из начала списка ребер, если ребро соединяет две разных компоненты связности то компоненты связности объединить в одну.

 Выбираем ребро с наименьшим весом.