
Билет №1 Нормальное и тангенциальное ускорение.
Нормальное ускорение:
![]()
или
![]()
где ![]() —
нормальное (центростремительное)
ускорение,
—
нормальное (центростремительное)
ускорение, ![]() —
(мгновенная) линейная скорость движения
по траектории,
—
(мгновенная) линейная скорость движения
по траектории, ![]() —
(мгновенная) угловая
скорость этого
движения относительно центра кривизны
траектории,
—
(мгновенная) угловая
скорость этого
движения относительно центра кривизны
траектории, ![]() —
радиус кривизны траектории в данной
точке. (Cвязь между первой формулой и
второй очевидна, учитывая
—
радиус кривизны траектории в данной
точке. (Cвязь между первой формулой и
второй очевидна, учитывая ![]() ).
).
Выражения
выше включают абсолютные величины. Их
легко записать в векторном виде, домножив
на ![]() —
единичный вектор от центра кривизны
траектории к данной ее точки:
—
единичный вектор от центра кривизны
траектории к данной ее точки:
![]()
![]()
Эти
формулы равно применимы к случаю движения
с постоянной (по абсолютной величине)
скоростью, так и к произвольному случаю.
Однако во втором надо иметь в виду, что
центростремительное ускорение не есть
полный вектор ускорения, а лишь его
составляющая, перпендикулярная траектории
(или, что то же, перпендикулярная вектору
мгновенной скорости); в полный же вектор
ускорения тогда входит еще и тангенциальная
составляющая (тангенциальное ускорение) ![]() ,
по направлению совпадающее с касательной
к траектории (или, что то же, с мгновенной
скоростью)[2].
,
по направлению совпадающее с касательной
к траектории (или, что то же, с мгновенной
скоростью)[2].
Тангенциальное ускорение:
Величину тангенциального ускорения - в смысле проекции вектора ускорения на единичный касательный вектор траектории - можно выразить так:
![]()
где ![]() -
путевая скорость вдоль траектории,
совпадающая с абсолютной величиной
мгновенной скорости в данный момент.
-
путевая скорость вдоль траектории,
совпадающая с абсолютной величиной
мгновенной скорости в данный момент.
Если
использовать для единичного касательного
вектора обозначение ![]() ,
то можно записать тангенциальное
ускорение в векторном виде:
,
то можно записать тангенциальное
ускорение в векторном виде:
![]()
---------------------------------------------------------------------------------------
Билет №2 Принцип относительности Галилея
![]()
Из
формулы для ускорений следует, что если
движущаяся система отсчета движется
относительно первой без ускорения, то
есть ![]() ,
то ускорение
,
то ускорение ![]() тела
относительно обеих систем отсчета
одинаково.
тела
относительно обеих систем отсчета
одинаково.
Поскольку в Ньютоновской динамике из кинематических величин именно ускорение играет роль (см.второй закон Ньютона), то, если довольно естественно предположить, что силы зависят лишь от относительного положения и скоростей физических тел (а не их положения относительно абстрактного начала отсчета), окажется, что все уравнения механики запишутся одинаково в любой инерциальной системе отсчета — иначе говоря, законы механики не зависят от того, в какой из инерциальных систем отсчета мы их исследуем, не зависят от выбора в качестве рабочей какой-то конкретной из инерциальных систем отсчета. Также — поэтому — не зависит от такого выбора системы отсчета наблюдаемое движение тел (учитывая, конечно, начальные скорости). Это утверждение известно как принцип относительности Галилея, в отличие от Принципа относительности Эйнштейна
Иным образом этот принцип формулируется (следуя Галилею) так: если в двух замкнутых лабораториях, одна из которых равномерно прямолинейно (и поступательно) движется относительно другой, провести одинаковый механический эксперимент, результат будет одинаковым.
Требование (постулат) принципа относительности вместе с преобразованиями Галилея, представляющимися достаточно интуитивно очевидными, во многом следует форма и структура ньютоновской механики (и исторически также они оказали существенное влияние на ее формулировку). Говоря же несколько более формально, они налагают на структуру механики ограничения, достаточно существенно влияющие на ее возможные формулировки, исторически весьма сильно способствовавшие ее оформлению.
---------------------------------------------------------------------------------------
Билет №3 Постулаты Эйнштейна. Преобразования Лоренца.
1 постулат Эйнштейна или принцип относительности: все законы природы инвариантны по отношению ко всем инерциальным системам отсчета. Все физические, химические, биологические явления протекают во всех инерциальных системах отсчета одинаково.
2 постулат или принцип постоянства скорости света: скорость света в вакууме постоянна и одинакова по отношении» к любым инерциальным системам отсчета. Она не зависит ни от скорости источника света, ни от скорости его приемника. Ни один материальный объект не может двигаться со скоростью, превышающей скорость света в вакууме. Более того, пи одна частица вещества, т.е. частица с массой покоя, отличной от нуля, не может достичь скорости света в вакууме, с такой скоростью могут двигаться лишь полевые частицы, т.е. частицы с массой покоя, равной нулю.
Если ИСО K' движется относительно ИСО K с постоянной скоростью v вдоль оси x, а начала пространственных координат совпадают в начальный момент времени в обеих системах, то преобразования Лоренца (прямые) имеют вид:
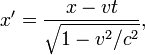
![]()
![]()
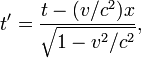
где c — скорость света, величины со штрихами измерены в системе K', без штрихов — в K.
Эта форма преобразования (то есть при выборе коллинеарных осей), называемая иногда бустом (англ. boost) или лоренцевским бустом (особенно в англоязычной литературе), несмотря на свою простоту, включает, по сути, всё специфическое физическое содержание преобразований Лоренца, так как пространственные оси всегда можно выбрать таким образом, а при желании добавить пространственные повороты не представляет трудности (см. это в явном развёрнутом виде ниже), хотя и делает формулы более громоздкими.
Формулы, выражающие обратное преобразование, то есть выражающие x',y',z',t' через x,y,z,t можно получить просто заменой v на − v (абсолютная величина относительной скорости движения систем отсчёта | v | одинакова при измерении её в обеих системах отсчёта, поэтому можно при желании снабдить v штрихом, только при этом надо внимательно следить за тем, чтобы знак и определение соответствовали друг другу) и взаимной заменой штрихованных x и t с нештрихованными. Или решая систему уравнений (1) относительно x',y',z',t'.
Надо иметь в виду, что в литературе преобразования Лоренца часто записывается для упрощения в системе единиц, где c = 1, что действительно делает их вид более изящным.
Видно, что при преобразованиях Лоренца события, одновременные в одной системе отсчёта, не являются одновременными в другой (относительность одновременности), кроме того, у движущегося тела сокращается продольный размер по сравнению с тем, какой оно имеет в сопутствующей ему системе отсчёта (лоренцево сокращение), а ход движущихся часов замедляется, если наблюдать их из «неподвижной» системы отсчёта (релятивистское замедление времени).
---------------------------------------------------------------------------------------
Билет №4 Релятивистский закон сложения скоростей
Непосредственным
следствием преобразований Лоренца
является релятивистское правило сложения
скоростей. Если некоторый объект имеет
компоненты скорости ![]() относительно
системы S и
относительно
системы S и ![]() —
относительно S', то между ними существует
следующая связь:
—
относительно S', то между ними существует
следующая связь:
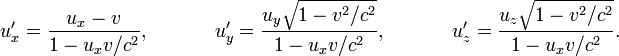
В
этих соотношениях относительна скорость
движения систем отсчёта v направлена
вдоль оси x. Релятивистское сложение
скоростей, как и преобразования Лоренца,
при малых скоростях (![]() )
переходит в классический закон сложения
скоростей.
)
переходит в классический закон сложения
скоростей.
Если
объект движется со скоростью света ![]() вдоль
оси x относительно системы S, то такая
же скорость у него будет и относительно
S':
вдоль
оси x относительно системы S, то такая
же скорость у него будет и относительно
S': ![]() .
Это означает, что скорость
.
Это означает, что скорость ![]() является
инвариантной (одинаковой) во всех ИСО.
является
инвариантной (одинаковой) во всех ИСО.
---------------------------------------------------------------------------------------
Билет №5 Сокращение длин и увеличение длительности событий- следствия из преобразований Лоренца
Если длину (форму) движущегося объекта определять при помощи одновременной фиксации координат его поверхности, то из преобразований Лоренца следует, что линейные размеры такого тела относительно «неподвижной» системы отсчёта сокращаются:
![]() ,
,
где ![]() —
длина вдоль направления движения
относительно неподвижной системы
отсчёта, а
—
длина вдоль направления движения
относительно неподвижной системы
отсчёта, а ![]() —
длина в движущейся системе отсчёта,
связанной с телом (т. н. собственная
длина тела). При этом сокращаются
продольные размеры тела (то есть
измеряемые вдоль направления движения).
Поперечные размеры не изменяются.
—
длина в движущейся системе отсчёта,
связанной с телом (т. н. собственная
длина тела). При этом сокращаются
продольные размеры тела (то есть
измеряемые вдоль направления движения).
Поперечные размеры не изменяются.
Такое сокращение размеров ещё называют лоренцевым сокращением. При визуальном наблюдении движущихся тел, дополнительно к лоренцевому сокращению необходимо учитывать время распространения светового сигнала от поверхности тела. В результате быстро движущееся тело выглядит повёрнутым, но не сжатым в направлении движения.
Замедление времени
Если
часы неподвижны в системе ![]() ,
то для двух последовательных событий
имеет место
,
то для двух последовательных событий
имеет место ![]() .
Такие часы перемещаются относительно
системы
.
Такие часы перемещаются относительно
системы ![]() по
закону
по
закону ![]() ,
поэтому интервалы времени связаны
следующим образом:
,
поэтому интервалы времени связаны
следующим образом:
![]()
Важно
понимать, что в этой формуле интервал
времени ![]() измеряется одними движущимися
часами
.
Он сравнивается с показаниями
измеряется одними движущимися
часами
.
Он сравнивается с показаниями ![]() нескольких различных,
синхронно идущих часов, расположенных
в системе
,
мимо которых движутся часы
.
В результате такого сравнения оказывается,
что движущиеся часы
идут
медленнее неподвижных часов. С этим
эффектом связан так называемый парадокс
близнецов.
нескольких различных,
синхронно идущих часов, расположенных
в системе
,
мимо которых движутся часы
.
В результате такого сравнения оказывается,
что движущиеся часы
идут
медленнее неподвижных часов. С этим
эффектом связан так называемый парадокс
близнецов.
Если
часы движутся с переменной
скоростью ![]() относительно
инерциальной системы отсчёта, то время,
измеряемое этими часами (т. н. собственное
время),
не зависит от ускорения, и может быть
вычислено по следующей формуле:
относительно
инерциальной системы отсчёта, то время,
измеряемое этими часами (т. н. собственное
время),
не зависит от ускорения, и может быть
вычислено по следующей формуле:
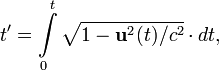
где при помощи интегрирования, суммируются интервалы времени в локально инерциальных системах отсчёта (т. н. мгновенно сопутствующих ИСО).
Относительность одновременности
Если
два разнесённых в пространстве события
(например, вспышки света) происходят
одновременно в движущейся системе
отсчёта ![]() ,
то они будут неодновременны относительно
«неподвижной» системы
.
При Δt'
= 0 из
преобразований Лоренца следует
,
то они будут неодновременны относительно
«неподвижной» системы
.
При Δt'
= 0 из
преобразований Лоренца следует
![]()
Если Δx = x2 − x1 > 0, то и Δt = t2 − t1 > 0. Это означает, что, с точки зрения неподвижного наблюдателя, левое событие происходит раньше правого (t2 > t1). Относительность одновременности приводит к невозможности синхронизации часов в различных инерциальных системах отсчёта во всём пространстве.
Пусть в двух системах отсчёта, вдоль оси x расположены синхронизированные в каждой системе часы, и в момент совпадения «центральных» часов (на рисунке ниже) они показывают одинаковое время.
Левый рисунок показывает, как эта ситуация выглядит с точки зрения наблюдателя в системе S. Часы в движущейся системе отсчёта показывают различное время. Находящиеся по ходу движения часы отстают, а находящиеся против хода движения опережают «центральные» часы. Аналогична ситуация для наблюдателей в S' (правый рисунок).
Билет №6 Интервал в СТО (Специальная Система Относительности)
Интервал- инвариант по отношению к переходу от одной системы отсчета к другой. Промежутки между ∆t и длины ∆l по отношению к такому переходу не являются инвариантами. Следовательно, каждое из слагаемых, образующих величину ∆s²=c²∆t²-∆l², изменяется при переходе от одной системы к другой; сама же величина ∆s² остаётся неизменной.
---------------------------------------------------------------------------------------
Билет №8 Законы Ньютона
I Существуют такие системы отсчёта, называемые инерциальными, относительно которых материальная точка при отсутствии внешних воздействий сохраняет величину и направление своей скорости неограниченно долго.
II В инерциальной системе отсчёта ускорение, которое получает материальная точка, прямо пропорционально равнодействующей всех приложенных к ней сил и обратно пропорционально её массе.
III Материальные точки попарно действуют друг на друга с силами, имеющими одинаковую природу, направленными вдоль прямой, соединяющей эти точки, равными по модулю и противоположными по направлению:
![]()
---------------------------------------------------------------------------------------
Билет №9 Гармонические колебания
Гармоническое колебание — явление периодического изменения какой-либо величины, при котором зависимость от аргумента имеет характер функции синуса или косинуса.
Свободные колебания совершаются под действием внутренних сил системы после того, как система была выведена из положения равновесия. Чтобы свободные колебания были гармоническими, необходимо, чтобы колебательная система была линейной (описывалась линейными уравнениями движения), и в ней отсутствовала диссипация энергии (последняя вызвала бы затухание).
Вынужденные колебания совершаются под воздействием внешней периодической силы. Чтобы они были гармоническими, достаточно чтобы колебательная система была линейной (описывалась линейными уравнениями движения), а внешняя сила сама менялась со временем как гармоническое колебание (т.е. чтобы зависимость от времени этой силы была синусоидальной).
---------------------------------------------------------------------------------------
Билет №10 Затухающие колебания
Затухающие
колебания —
колебания, энергия которых уменьшается
с течением времени. Бесконечно длящийся
процесс вида ![]() в
природе невозможен. Свободные колебания
любого осциллятора рано или поздно
затухают и прекращаются. Поэтому на
практике обычно имеют дело с затухающими
колебаниями. Они характеризуются тем,
что амплитуда колебаний A является
убывающей функцией. Обычно затухание
происходит под действием сил сопротивления
среды, наиболее часто выражаемых линейной
зависимостью от скорости колебаний
в
природе невозможен. Свободные колебания
любого осциллятора рано или поздно
затухают и прекращаются. Поэтому на
практике обычно имеют дело с затухающими
колебаниями. Они характеризуются тем,
что амплитуда колебаний A является
убывающей функцией. Обычно затухание
происходит под действием сил сопротивления
среды, наиболее часто выражаемых линейной
зависимостью от скорости колебаний ![]() или
её квадрата.
или
её квадрата.
В акустике: затухание — уменьшение уровня сигнала до полной неслышимости.
---------------------------------------------------------------------------------------
Билет №11 Вынужденные колебания
Вынужденные колебания — колебания, происходящие под воздействием внешних сил, меняющихся во времени.
Автоколебания отличаются от вынужденных колебаний тем, что последние вызваны периодическим внешним воздействием и происходят с частотой этого воздействия, в то время как возникновение автоколебаний и их частота определяются внутренними свойствами самой автоколебательной системы.
Наиболее
простой и содержательный пример
вынужденных колебаний можно получить
из рассмотрения гармонического
осциллятора и
вынуждающей силы, которая изменяется
по закону: ![]() .
.
---------------------------------------------------------------------------------------
Билет №12 Масса, импульс, энергия в СТО
Если
частица с массой m движется со скоростью ![]() ,
то её энергия и импульс имеют следующую
зависимость от скорости:
,
то её энергия и импульс имеют следующую
зависимость от скорости:

Эти
соотношения обобщают классические
выражения для энергии и импульса,
получающиеся в результате разложения
в ряд по ![]() :
:
![]()
При
нулевой скорости, энергия частицы
называется энергией покоя: ![]() .
В современной физической литературе,
принято, что m —
масса частицы не
зависит от скорости, являясь инвариантом
относительно преобразований Лоренца,
и является величиной неаддитивной.
Понятие «релятивистской массы», зависящей
от скорости
.
В современной физической литературе,
принято, что m —
масса частицы не
зависит от скорости, являясь инвариантом
относительно преобразований Лоренца,
и является величиной неаддитивной.
Понятие «релятивистской массы», зависящей
от скорости ![]() не
используется [25] ,
хотя оно и встречается в ранних работах
по теории относительности. Историческая
причина введения этого понятия была
связана с попытками сохранить для
релятивистского импульса классическую
форму:
не
используется [25] ,
хотя оно и встречается в ранних работах
по теории относительности. Историческая
причина введения этого понятия была
связана с попытками сохранить для
релятивистского импульса классическую
форму: ![]() .
.
При приближении скорости тела к скорости света, его энергия и импульс стремятся к бесконечности. Это одна из причин, по которой «обычные» объекты неспособны двигаться быстрее скорости света. Для частицы с ненулевой массой даже достижение скорости света потребует затраты бесконечной энергии. Заметные отклонения от классических выражений для энергии и импульса происходят при скоростях близких к скорости света. Если скорости относительно невелики, то отклонения от классической динамики незначительны. Например, при скорости u=c/4, относительная разница релятивистского и классического импульса составляет всего 3 %.
Между релятивистской энергией и импульсом существуют следующие связи:
![]()
Эти формулы остаются справедливыми и для объектов, движущихся со скоростью света. В этом случае их масса должна быть равна нулю m = 0.
---------------------------------------------------------------------------------------
Билет №13 Закон сохранения энергии
Закон сохранения механической энергии может быть выведен из второго закона Ньютона[5], если учесть, что в консервативной системе все силы, действующие на тело, потенциальны и, следовательно, могут быть представлены в виде
![]() ,
,
где ![]() —
потенциальная энергия материальной
точки (
—
потенциальная энергия материальной
точки (![]() — радиус-вектор точки
пространства). В этом случае второй
закон Ньютона для одной частицы имеет
вид
— радиус-вектор точки
пространства). В этом случае второй
закон Ньютона для одной частицы имеет
вид
![]() ,
,
где m — масса частицы, ![]() — вектор её скорости. Скалярно
домножив обе
части данного уравнения на скорость
частицы и приняв во внимание, что
— вектор её скорости. Скалярно
домножив обе
части данного уравнения на скорость
частицы и приняв во внимание, что ![]() ,
можно получить
,
можно получить
![]()
Путём элементарных операций это выражение может быть приведено к следующему виду
![]()
Отсюда непосредственно следует, что выражение, стоящее под знаком дифференцирования по времени, сохраняется. Это выражение и называется механической энергией материальной точки. Первый член в сумме отвечает кинетической энергии, второй — потенциальной.
Этот вывод может быть легко обобщён на систему материальных точек[2].
---------------------------------------------------------------------------------------
Билет №14 Консервативные и диссипативные силы. Связь консервативной силы и потенциальной энергии.
В физике консервати́вные си́лы (потенциальные силы) — силы, работа которых не зависит от формы траектории (зависит только от начальной и конечной точки приложения сил). Отсюда следует определение: консервативные силы — такие силы, работа которых по любой замкнутой траектории равна 0.
Если в системе действуют только консервативные силы, то механическая энергия системы сохраняется.
Для консервативных сил выполняются следующие тождества:
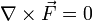 — ротор консервативных
сил равен 0;
— ротор консервативных
сил равен 0;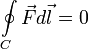 — работа консервативных
сил по произвольному замкнутому контуру
равна 0;
— работа консервативных
сил по произвольному замкнутому контуру
равна 0;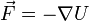 —
консервативная
сила является градиентом некой скалярной
функции U,
называемой силовой. Эта функция
равна потенциальной
энергии взятой
с обратным знаком.
—
консервативная
сила является градиентом некой скалярной
функции U,
называемой силовой. Эта функция
равна потенциальной
энергии взятой
с обратным знаком.
В школьной программе по физике силы разделяют на консервативные и неконсервативные. Примерами консервативных сил являются: сила тяжести, сила упругости. Примерами неконсервативных сил являются сила трения и сила сопротивления среды.
В теоретической физике выделяют только четыре типа сил, каждая из которых является консервативной
Диссипати́вные си́лы — силы, при действии которых на механическую систему её полная механическая энергия убывает (то есть диссипирует), переходя в другие, немеханические формы энергии, например, в теплоту. В отличие от потенциальных сил зависят не только от взаимного расположения тел, но и от их относительных скоростей
Примеры сил:
Силы вязкого или сухого трения.
Сила трения скольжения
---------------------------------------------------------------------------------------
Билет №15 Закон сохранения импульса
Зако́н сохране́ния и́мпульса (Зако́н сохране́ния количества движения) утверждает, что векторная сумма импульсов всех тел (или частиц)замкнутой системы есть величина постоянная.
В классической механике закон сохранения импульса обычно выводится как следствие законов Ньютона. Из законов Ньютона можно показать, что при движении в пустом пространстве импульс сохраняется во времени, а при наличии взаимодействия скорость его изменения определяется суммой приложенных сил.
Как и любой из фундаментальных законов сохранения, закон сохранения импульса описывает одну из фундаментальных симметрий, — однородность пространства.
Рассмотрим выражение определения силы
![]()
Перепишем его для системы из N частиц:
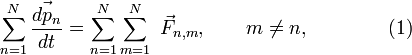
где
суммирование идет по всем силам,
действующим на n-ю
частицу со стороны m-ой.
Согласно третьему закону Ньютона, силы
вида ![]() и
и ![]() будут
равны по абсолютному значению и
противоположны по направлению, то
есть
будут
равны по абсолютному значению и
противоположны по направлению, то
есть ![]() Тогда
после подстановки полученного результата
в выражение (1) правая часть будет равна
нулю, то есть:
Тогда
после подстановки полученного результата
в выражение (1) правая часть будет равна
нулю, то есть:
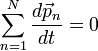
или
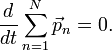
Как известно, если производная от некоторого выражения равна нулю, то это выражение есть постоянная величина относительно переменной дифференцирования, а значит:
 (постоянный
вектор).
(постоянный
вектор).
То есть суммарный импульс системы частиц есть величина постоянная. Нетрудно получить аналогичное выражение для одной частицы.
Следует учесть, что вышеприведенные рассуждения справедливы лишь для замкнутой системы.
Также
стоит подчеркнуть, что изменение
импульса ![]() зависит
не только от действующей на тело силы,
но и от продолжительности её действия.
зависит
не только от действующей на тело силы,
но и от продолжительности её действия.
---------------------------------------------------------------------------------------
Билет №16 Закон сохранения момента импульса
Зако́н сохране́ния моме́нта и́мпульса (закон сохранения углового момента) — векторная сумма всех моментов импульса относительно любой оси для замкнутой системы остается постоянной в случае равновесия системы. В соответствии с этим, момент импульса замкнутой системы относительно любой неподвижной точки не изменяется со временем.
Закон сохранения момента импульса есть проявление изотропности пространства.
---------------------------------------------------------------------------------------
Билет №17 Второй закон Ньютона для вращательного движения
---------------------------------------------------------------------------------------
Билет №18 Вычисление моментов инерции твердых тел
Тонкостенный цилиндр
![]()
Толстостенный цилиндр
![]()
Однородный диск
![]()
Сплошной конус
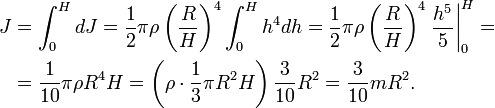
Сплошной однородны шар
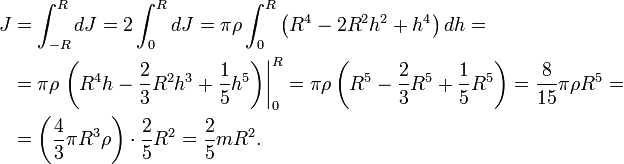
Тонкостенная сфера
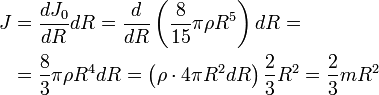
Тонкий стержень(ось проходит через центр)
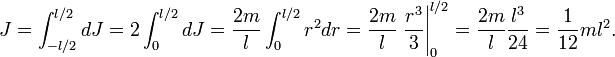
Тонкий стержень(ось проходит через конец)
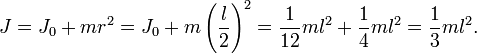
---------------------------------------------------------------------------------------
Билет №19 Физический маятник
Физический маятник — осциллятор, представляющий собой твёрдое тело, совершающее колебания в поле каких-либо сил относительно точки, не являющейся центром масс этого тела, или неподвижной оси, перпендикулярной направлению действия сил и не проходящей через центр масс этого тела.
Пренебрегая сопротивлением среды, дифференциальное уравнение колебаний физического маятника в поле силы тяжести записывается следующим образом:
![]() .
.
Полагая ![]() ,
предыдущее уравнение можно переписать
в виде:
,
предыдущее уравнение можно переписать
в виде:
![]() .
.
Последнее
уравнение аналогично уравнению
колебаний математического
маятника длиной ![]() .
Величина
называется приведённой
длиной физического
маятника.
.
Величина
называется приведённой
длиной физического
маятника.
