40. Поиск путей в графе. Алгоритм Терри нахождения пути в графе. Алгоритм поиска пути минимальной длины(«фронта волны)

АЛГОРИТМ ТЕРРИ ПОИСКА ЦЕПИ, СОЕДИНЯЮЩЕЙ ЗАДАННЫЕ ВЕРШИНЫ a и b в неориентированном графе G:(11 номер из курсовой)

Если исходя из вершины a, и осуществляя последовательный переход от каждой достигнутой вершины, к смежной ей вершине руководствоваться след. правилами:10 20 30 40 то можно всегда найти цепь, соед. заданные вершины a и b

в связном графе G.

10 Идти по произвольному ребру, отмечая всякий раз направление в котором оно было пройдено.

20 Исходя из некоторой вершины хi всегда следовать только по тому ребру, которой не было пройдено или было пройдено в противоположном направлении

30 Для всякой вершины xi отмечать входящие в xi ребра, если вершина xi встретилась первый раз.

40 По первому входящему ребру идти лишь тогда, когда нет других возможностей.

Замечание: Путь из вершины a в вершину a, все ребра которого пройдены дважды выделяет в графе компоненту связности.

АЛГОРИТМ ФРОНТА ВОЛНЫ ПОИСКА МИНИМАЛЬНОГО ПУТИ ИЗ ВЕРШИНЫ a в b в орграфе G: (12 номер из курсовой)

10 Помечаем вершину а индексом 0, а все вершины, принадлежащие образу вершины а Г(а) индексом 1. Множество вершин, помеченных индексом 0, 1 обозначаем FW0(a) FW1(A) Полагаем k:=1

20 Если FWk(a)=∅ или при k=n-1 b∉FWn-1(a), то вершина b недостижима из a и алгоритм заканчивает свою работу(выход). В противном случае ( FWk(a)≠∅) переходим к шагу 30

30 Если ?b∈FWk(a)?, то переходим к шагу 40, в противном случае (?) существует путь из а в b длины k и этот путь минимален. Он задается последовательностью вершин. a=x0 x1 x2 .... xk-2 xk-1 xk=b, где xk-1∈FWk-1(a)∧Г-1(b);

xk-2∈FWk-2(a)∧Г-1(xk-1);....; x1∈FW1(a)∧Г-1(x2); на этом алгоритм заканчивает свою работу(выход)

40 Помечаем индексом k+1 все непомеченные вершины, которые принадлежат образу множества вершин помеченных индексом k. Множество вершин с индексом k+1 обозначаем Wk+1(a). Полагаем k:=k+1 и переходим в шагу два.

Замечание1: FWk(a) - фронт волны k-ого уровня.

Замечание2: Вершины х1х2...хk-2,xk-1 вообще говорят могут быть выделенны неоднозначно, т.е. может существовать несколько минимальных путей.

Замечание3: FWk+1(a) отыскивается по рекурентной форме:

FWk+1=Г(FWk(a))\ ∨i=0KFWi(a).

41.Алгоритм Форда и Форда-Беллмана нахождение минимального пути в нагруженном графе.

Алгоритм Форда

Помечаем вершину xi индексом λi; Полагаем a=x6 и присваиваем ей λ6, причем λ0=0, а все остальные вершины помечаем λj=∞.

Помечаем <xi,xj> для которой λi- λj˃l(xi,xj), затем заменяем индекс λj на индекс λ/J; λ/J= λi+ l(xi,xj)< λj

Продолжаем процесс до тех пор пока не перестанут уменьшаться индексы.

Предположим что алгоритм Форда выполним, тогда λn= λρ0.

Среди дуг будет та по которой алгоритм Форда применим:

λn- λρ1= l(x ρ1, xn)

λ ρ1- λρ2= l(x ρ1, x ρ1)

…………………

λ ρk- λ0= l(x 0, x ρk)

________________ (сложим все эти равенства)

λ n= l(x 0, x ρk…………. x n).

Возьмем x 0, x k1…………. x n предположим что он короче чем тот который мы нашли по алгоритму Форда: Λ0, λк1……………………………………………. λкn, -индексы присвоены по алгоритму Форда, где выполняется:

Λk1- λ0≤ l(x 0, xr1)

λ k2- λk1≤ l(x k1, x k2)

…………………

λ n- λks≤ l(x ks, x n)

________________ (сложим все эти равенства)

λ n≤l(x 0, x k…………. x n). значит метод Форда минимальный путь.

Алгоритм Форда-Беллмана.

Замечание: он позволяет по таблице значений λ(к)i (i=1…..n) , (k=0,1……..n-1) и матрицы длин дуг нагруженного орграфа определить минимальный путь из вершины а в любую достижимую вершину, причем из всех возможных путей он выделяет путь с наименьшим числом дуг.

λ(к)i=

Замечание: к=0,1…………….n-1 , λ1(к)=0; λ(0)i=∞, i=2,3…….n.

Матрицу весов С опишем следующим образом

Cij=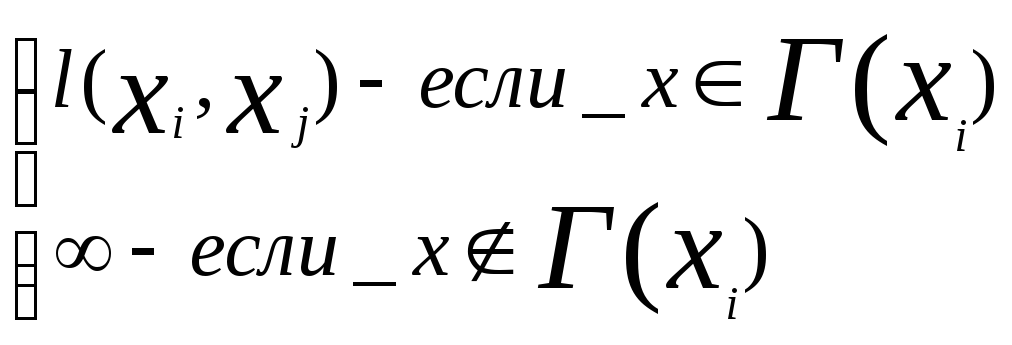

алгоритм Форда-беллмана это модифицированный алгоритм Форда для матрицы весов дуг С, который может быть записан в виде:

λ(к+1)j=