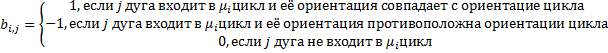- •1. Понятие множества. Способы задания множеств. Операции над множествами. Диаграммы Венна.
- •3. Прямое произведение множеств. Отношения, бинарные отношения. Операции над отношениями.
- •4. Понятие функции. Инъективные, биективные, суръективные функции. Композиция и обращение функций.
- •5. Бинарные отношения на множестве х. Рефлексивность, симметричность, транзитивность бинарных отношений на множестве х.
- •6. Отношение эквивалентности. Класс эквивалентности.
- •7. Разбиение множества. Теорема о связи между отношением эквивалентности на множестве и разбиением множества.
- •8. Отношение порядка. Частичный и линейный порядок. Упорядоченные множества.
- •9. Мощьность множества. Счётные множества. Несчётные множества. Теорема Кантора.
- •10. Понятие нечёткого множества. Виды и некоторые свойства нечётких множеств. Способы задания нечётких множеств.
- •11.Функции принадлежности нечётких множеств и методы их построения.
- •12.Равенство нечётких множеств. Нечёткое подмножество.
- •13. Операции с нечёткими множествами. Некоторые дополнительные операции над нечёткими множествами.
- •15. Определение нечёткого отношения. Виды нечётких отношений. Способы задания нечётких отношений.
- •16. Равенство нечётких отношений. Нечёткое доминирование. Операции с нечёткими отношениям.
- •17. Свойства бинарных нечётких отношений заданных на базисном множестве х.
- •18.Высказывания. Логические операции. Язык логики высказываний. Формулы логики высказывания.
- •20. Формулы логики высказываний. Равносильность формул логики высказываний. Основные равносильности.
- •21. Двойственность. Закон двойственности. Пример.
- •22. Тождественно-истинные и тождественно-ложные формулы. Выполнимость и опровержимость формул. Пример. Правильные рассуждения.
- •23. Отношение логического следования. Правильные рассуждения. Примеры.
- •24. Нормальные формы формул. Приведение к днф и кнф.
- •25. Нормальные формы формул. Приведение к сднф и скнф.
- •26.Булевы функции. Теорема о представлении булевой функции формулой логики высказываний.
- •27. Булевы функции. Булевы функции двух переменных.
- •28.Представление булевых функций формулой логики высказываний в сднф и в скнф. Примеры.
- •29. Полные системы булевых функций. Теорема о сведении полноты одной системы булевых функцийк другой. Примеры полных систем.
- •31.Функционально-замкнутые классы. Классы t0,t1,s,l,m. Теорема Поста(доказательство по необходимому признаку). Док-ва у меня нет
- •32.Описание переключательных схем с помощью формул логики высказываний. Анализ, упрощение и синтез переключательных схем.
- •33.Понятие о проблеме минимизации булевых функций в классе днф.
- •34.Предикаты. Кванторы. Язык логики предикатов. Формулы логики предикатов. Равносильность и общезначимость формул логики предикатов. Основные равносильности.
- •35.Понятие интерпретации. Равносильность и общезначимость формул логики предикатов. Приведенная нормальная формула логики предикатов. Проблема разрешимости. Формулировка теоремы Черча.
- •36.Ориентированные и неориентированные графы. Основные понятия.
- •37.Матричное задание графа. Матрицы сложности и инциденций. Цикломатическая матрица.
- •38. Пути в графе. Цепи. Связные графы и компоненты связности.
- •39.Специальные пути в графе. Понятие о плоских графах.
- •40. Поиск путей в графе. Алгоритм Терри нахождения пути в графе. Алгоритм поиска пути минимальной длины(«фронта волны)
- •41.Алгоритм Форда и Форда-Беллмана нахождение минимального пути в нагруженном графе.
- •42.Деревья. Свойства деревьев. Цикломатическое число. Остовные деревья графа. Алгоритм нахождения остовного дерева.
- •43.Вектор-циклы. Пространство вектор циклов. Независимые циклы. Цикломатическое число. Алгоритм нахождения базис вектор-циклов.
- •44.Цикломатическая (контурная) матрица и матрица инциденций. Законы Киргофа. Уравнение контурных токов. Примеры.
- •45.Транспортные сети. Поток в сети. Полный и максимальный поток. Алгоритмы нахождения полного и максимального потока.
36.Ориентированные и неориентированные графы. Основные понятия.
ОРИЕНТИРОВАННЫЕ ГРАФЫ.(ОРГРАФЫ)
Пусть Х не пустое множество, а Х2=Х×Х - множество всех его пар.
О: Пара <Г,Х>=G называется ориентированным графом(орграфом), где Г-произвольное подмножество множества Х2 (Г⊆Х2)
Элементы х∈Х называются вершинами, а пара <X,Y>∈Г дугами орграфа.
Замечание: тройку множеств <Г,Х,Y>, где Г⊆Х,Y называют многозначным отображателем из множества Х во множестве У. Обозначают Г:Х+Y.
При этом, если х∈Х, то множество Г(х)={y∈Y|<x,y>∈Г}⊆Y называют образом элемента х, а Г-1(y)={x∈X|<x,y>∈Г}⊆X называют прообразом y.
Если А⊆Х, то Г(А)=∨х∈АГ(х) - это образ множества А
А⊆Y, то Г-1(А)=∨y∈AГ-1(А) - это прообраз мн-ва А
Пусть задан орграф G=<Г,Х>
1. если y∈Г(х), т.е. <x,y> дуга, то говорят что она исходит из вершины х и заходит в у.
2. Дуга называется инцидентной в вершине х, если она заходит в х или исходит из х.
3. Дуга <x,х> называется петлей.
4. Вершина, не имеющая инцидентных дуг называется изолированной. Две вершины называются смежными, если существует дуга инцидентная им обоим.
Пути в орграфе.
О1: Последовательность дуг орграфа такая что начало каждой последующей дуги совпадает с концом предыдущей называется путем.
О2: Путь у которого начало первой дуги совпадает с концом последней называется замкнутым путем, или контуром.
О3: Путь (контур) называется элементарным, если все его вершины различны за исключением первой и последней.
О4:Путь (контур) называется простым, если все его дуги различны.
Примеры:
1) <x1,x2> <x2,x5> <x5,x4> - не контур, но простой эл-ый путь.
2) <x1,x2> <x2,x3> <x3,x1> - эл-ый простой путь, контур.
3) <x1,x2> <x2,x5> <x5,x4> <x4,x2> <x2,x3> <x3,x1> - контур, простой, не эл-ый
4) <x1,x2> <x2,x3> <x3,x1> <x1,x2> <x2,x3> <x3,x1> - не простой, не эл-ый, контур
5) <x1,x2> <x2,x5> <x5,x4> <x4,x2> <x2,x3> - не путь
НЕОРИЕНТИРОВАННЫЕ ГРАФЫ
Пусть Х-непустое множество. Х(2) - мн-во всех 2-х элементарных подмножеств множества Х.
Пример: Х={1,2,3}. X(2)={{1,2},{1,3},{2,3}}
О: Пара <Q,X>=G, где Q произвольное подмножество множества Х (Q⊆X) называется неориентированным графом. Элементы х∈Х - вершинами, а элементы {x,y}∈Q - (неупорядоченные пары) - ребрами.
Замечание: неориентированные графы можно изучать как графы симметричных бинарных отношений.
Подграфом графа G называется G’, если X’⊂X, Q’⊂Q (Г’⊂Г), а в случае если X’=X, то подграфом называют частичным графом.
О1: Цепью неориентированного графа называется последотельность ребер, которая может быть перемещена в путь введением соответствующей ориентации на её ребрах.
О2: Циклом называется цепь у которой 1-ая вершина совпадает с последней.
О3: Цепь (цикл) называется элементарной, если некоторая вершина встречается в ней не более одного раза.
О4: Цепь (цикл) называется простой, если некоторой ребро встречается в ней не более одного раза.
37.Матричное задание графа. Матрицы сложности и инциденций. Цикломатическая матрица.
G=<Г,х> , |x|=n , x={![]()
![]()
![]()
Пример:


Для вершины ![]() её полустепенью захода называется число
её полустепенью захода называется число
![]() ,
заходящих в неё дуг, а число
,
заходящих в неё дуг, а число ![]() полустепенью исхода исходящих дуг.
полустепенью исхода исходящих дуг.
![]() – называется степенью вершины.
– называется степенью вершины.
Замечание: для неориентированных графов матрица смежностей является симметричными, а элементы определиться следующим образом:
1 – существует ребро.
0 – в остальных случаях.
Степень – число инцыдентных вершине рёбер.
Матрица инциденций:
G=<Г,х> , |x|=n , |Г|=N, x={![]()
Пусть граф не имеет петель.
![]()
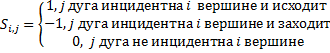
Замечание: для неориентированного графа инциденты определяются следующим образом:
![]()
Цикломатическая матрица:
G=<Q,x> - неор. граф.
n- вершины, N – ребра.
![]() - простые элементарные циклы, преобразуем
в орграф:
- простые элементарные циклы, преобразуем
в орграф: ![]()
![]()