
- •Вопрос 1. Методы математических доказательств (метод непосредственной проверки, метод доказательства от противного, метод математической индукции).
- •2 Метод.
- •3 Метод.
- •Вопрос 2. Формула Бинома Ньютона.
- •Вопрос 3. Сочетания, размещения, перестановки. Теоремы о числе сочетаний, размещений и перестановок, их следствия.
- •Вопрос 4. Инверсии в перестановках. Чётные и нечётные перестановки при транспозиции.
- •Вопрос 5. Понятие множества. Основные операции на множествах. Свойства операций на множестве (ассоциативность, коммутативность, дистрибутивность). Декартово произведение множеств.
- •Вопрос 6. Отображения множеств. Свойства отображений.
- •Вопрос 7. Отношения на множестве, бинарные отношения. Отношения эквивалентности, отношения порядка.
- •Вопрос 8. Понятия группоида, полугруппы, группы и подгруппы. Совпадение нейтрального (единичного) и симметричного (обратного) элементов группы и подгруппы.
- •Вопрос 9. Подгруппа, порожденная подмножеством элементов группы.
- •Вопрос 10. Понятие наибольшего общего делителя (нод) и наименьшего общего кратного (нок) целых чисел. Условия существования и единственности нод. Взаимно простые числа и их свойства.
- •Вопрос 11. Алгоритм Евклида для целых чисел.
- •Вопрос 12. Представление нод двух чисел в виде их линейной комбинации:
- •Вопрос 13. Простые числа, их свойства. Основная теорема арифметики. Каноническое разложение целого числа.
- •Вопрос 14. Бесконечность множества простых чисел.
- •Вопрос 15. Понятие изоморфизма групп. Теорема о изоморфизме цикличных групп одного и того же порядка.
- •Вопрос 16. Критерий «быть подгруппой», следствия. Пересечение подгрупп.
- •Вопрос 17. Смежные классы. Теорема Лагранжа.
- •Вопрос18: Разложение подстановки в произведение независимых циклов. Цикловая структура подстановки.
- •Вопрос 19: Теоремы о гомоморфизме групп.
- •Вопрос 20. Обращение теоремы Лагранжа для циклических групп.
- •Вопрос 21. Классы сопряженных элементов, их свойства. Нормализатор элемента группы.
- •Вопрос 22. Группа биективных отображений множества (симметрическая группа). Определение группы подстановок. Сопряжённые элементы в симметрической группе.
- •Вопрос 23. Знакопеременная группа.
- •Вопрос 24. Циклические группы, их описание. Цикличность подгруппы циклической группы. Пример группы корней n-ой степени из единицы.
- •Вопрос 25. Порядок элемента конечной группы. Соотношения между порядком элемента и порядком группы.
Вопрос 14. Бесконечность множества простых чисел.
Пусть конечно: p1,p2,p3, …pk – все простые.
Но тогда число p1*p2*p3* …*pk +1 не делится ни на одно простое, значит тоже простое.
Нашли еще одно. Противоречие.
Вопрос 15. Понятие изоморфизма групп. Теорема о изоморфизме цикличных групп одного и того же порядка.
Группы
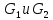 называют изоморфными, если между их
элементами можно установить взаимно
однозначное соответствие, сохраняющее
групповую операцию т.е. такое, что для
называют изоморфными, если между их
элементами можно установить взаимно
однозначное соответствие, сохраняющее
групповую операцию т.е. такое, что для
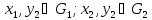 :
:
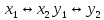 ;
;
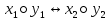
Т.е.
есть
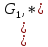 если выполнено:
если выполнено:
1)
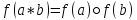 .
.
2)
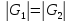
Th. о изоморфизме цикличных групп одного и того же порядка (вариант 1):
Любая
конечнопорождённая абелева группа G
изоморфна прямому произведению простых
циклических групп и бесконечных
циклических групп, где простая циклическая
группа это такая циклическая группа
чей порядок является степенью простого
числа. Что значит, что каждая такая
группа изоморфна группе вида
![]() ,
где n≥0,
и числа m1,...,mt
являются (не обязательно различными)
степенями простых чисел. Значения
n,m1,...,mt
однозначно определены (с точностью до
порядка) группой G;
В частности, G
конечна тогда и только тогда когда n
= 0.
,
где n≥0,
и числа m1,...,mt
являются (не обязательно различными)
степенями простых чисел. Значения
n,m1,...,mt
однозначно определены (с точностью до
порядка) группой G;
В частности, G
конечна тогда и только тогда когда n
= 0.
На
основании того факта что Gm
будет изоморфно произведению Gj
и Gk
тогда и только тогда когда j
и k
взаимнопросты и m
= jk,
мы также можем представить любую
конечнопорождённую группу G
в форме прямого произведения
![]() ,
,
где k1 делит k2, который делит k3 и так далее до ku. И снова, числа n и k1,...,ku однозначно заданы группой G.
Th. о изоморфизме цикличных групп одного и того же порядка (вариант 2):
Все циклы группы одного и того же порядка изоморфны.
Если
<g> образующая циклической группы
f: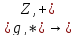

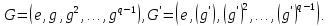
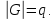
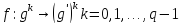
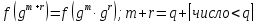
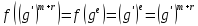
если
e>q
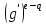
Вопрос 16. Критерий «быть подгруппой», следствия. Пересечение подгрупп.
Определение 1:
Непустое подмножество H группы (G, •) называют ее подгруппой, если H замкнуто относительно групповой
операции и является группой относительно этой операции. В этом случае пишут H < (G, •) или H < G, и если H ∉ {G, {е}}, то подгруппу H называют собственной. Очевидно, что всякая подгруппа в (G, •) является подполугруппой, но обратное неверно, как показывает пример подполугруппы N в (Z, +). Ясно также, что если H < (G, •), М < (H, •), то М < (G, •).
Теорема (Критерий подгруппы):
Непустое подмножество Н группы (G, ) является ее подгруппой тогда и только тогда, когда для любых элементов x и y из H элементы x*y и x| принадлежат H, т.е. H ≤ G (x ∊ H,y ∊ H => x*y ∊ H,x| ∊ H) .
Доказательство:
Если Н < (G, ), то условие следует из определения подгруппы. Пусть условие верно. Так как Н не пусто, то существует g ∊ Н и в силу условия е = g g-1 ∊ Н. Тогда для любых g , h ∊ H справедливы соотношения
h-1 = eh-1 ∊ Н и gh = g(h-1)-1 ∊ Н. Следовательно, подмножество Н замкнуто относительно групповой операции на G, и так как эта операция ассоциативна, то Н удовлетворяет всем условиям определения т е Н < (G, ).
Следствие 1:
Конечное непустое подмножество Н группы G является ее подгруппой тогда и только тогда, когда:
Vg,h ∊ H (g,h ∊ H),
т.е. тогда и только тогда, когда Н — подполугруппа в (G, ).
Следствие 2:
Пусть φ (G, ) —> (K, ) гомоморфизм групп. Тогда
а) Если Н < G, то φ(Н) < К,
б) если L < K, то φ-1(L) < G.
Доказательство:
a) Для любых α,β ∊ φ(Н) существуют a,b ∊ H такие, что φ(a) = α, φ(b) = β. Так как a b-1 ∊ H и φ(b-1) = φ(b)-1,
αβ-1 = φ(a) φ(b)-1 = φ(ab-1) ∊ φ(H).
б)Если a,b ∊ φ-1(L), то φ(a), φ(b) ∊ L и φ(a)φ(b)-1 ∊ L. Поэтому φ(ab-1) = φ(a) φ(b)-1 ∊ L, т.е. ab-1 ∊ φ-1(L).
Определение2:
Если
А и В – подгруппы группы G,
то А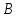 является подгруппой группы G.
является подгруппой группы G.
Доказательство:
(x
∊
А ,
y ∊
А
,
y ∊
А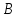 )
=> (x ∊
A, y ∊ A, x ∊ B, y ∊ B) => (x*y ∊ A, x|
∊ A, x*y ∊ B, y|
∊
B)
=> (x*y ∊ А
)
=> (x ∊
A, y ∊ A, x ∊ B, y ∊ B) => (x*y ∊ A, x|
∊ A, x*y ∊ B, y|
∊
B)
=> (x*y ∊ А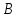 ,
x|
∊
А
,
x|
∊
А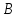 ).
).
