
- •Вопрос 1. Методы математических доказательств (метод непосредственной проверки, метод доказательства от противного, метод математической индукции).
- •2 Метод.
- •3 Метод.
- •Вопрос 2. Формула Бинома Ньютона.
- •Вопрос 3. Сочетания, размещения, перестановки. Теоремы о числе сочетаний, размещений и перестановок, их следствия.
- •Вопрос 4. Инверсии в перестановках. Чётные и нечётные перестановки при транспозиции.
- •Вопрос 5. Понятие множества. Основные операции на множествах. Свойства операций на множестве (ассоциативность, коммутативность, дистрибутивность). Декартово произведение множеств.
- •Вопрос 6. Отображения множеств. Свойства отображений.
- •Вопрос 7. Отношения на множестве, бинарные отношения. Отношения эквивалентности, отношения порядка.
- •Вопрос 8. Понятия группоида, полугруппы, группы и подгруппы. Совпадение нейтрального (единичного) и симметричного (обратного) элементов группы и подгруппы.
- •Вопрос 9. Подгруппа, порожденная подмножеством элементов группы.
- •Вопрос 10. Понятие наибольшего общего делителя (нод) и наименьшего общего кратного (нок) целых чисел. Условия существования и единственности нод. Взаимно простые числа и их свойства.
- •Вопрос 11. Алгоритм Евклида для целых чисел.
- •Вопрос 12. Представление нод двух чисел в виде их линейной комбинации:
- •Вопрос 13. Простые числа, их свойства. Основная теорема арифметики. Каноническое разложение целого числа.
- •Вопрос 14. Бесконечность множества простых чисел.
- •Вопрос 15. Понятие изоморфизма групп. Теорема о изоморфизме цикличных групп одного и того же порядка.
- •Вопрос 16. Критерий «быть подгруппой», следствия. Пересечение подгрупп.
- •Вопрос 17. Смежные классы. Теорема Лагранжа.
- •Вопрос18: Разложение подстановки в произведение независимых циклов. Цикловая структура подстановки.
- •Вопрос 19: Теоремы о гомоморфизме групп.
- •Вопрос 20. Обращение теоремы Лагранжа для циклических групп.
- •Вопрос 21. Классы сопряженных элементов, их свойства. Нормализатор элемента группы.
- •Вопрос 22. Группа биективных отображений множества (симметрическая группа). Определение группы подстановок. Сопряжённые элементы в симметрической группе.
- •Вопрос 23. Знакопеременная группа.
- •Вопрос 24. Циклические группы, их описание. Цикличность подгруппы циклической группы. Пример группы корней n-ой степени из единицы.
- •Вопрос 25. Порядок элемента конечной группы. Соотношения между порядком элемента и порядком группы.
Вопрос 5. Понятие множества. Основные операции на множествах. Свойства операций на множестве (ассоциативность, коммутативность, дистрибутивность). Декартово произведение множеств.
Определение 1:
Множество — это совокупность (собрание, семейство) каких-либо реально существующих или
мыслимых объектов, объединенных по некоторому признаку. Предполагается, что объекты, входящие в множество, попарно различны. Объекты, из которых составлено множество, называются его элементами. Множества и элементы множеств обозначаются различными буквами без индексов и с индексами. При этом, как правило, множества и элементы отождествляются с их обозначениями.
Определение 2:
Объединением множеств А, В называется множество A U В, состоящее из всех тех элементов, каждый из которых принадлежит хотя бы одному из множеств А, В. А U В = {m:m € A или m € B}
Определение 3:
Пересечением множеств А, В называется множество А∏В, состоящее из всех тех элементов, которые содержатся в обоих множествах А, В. A∏B = {m:m € A и m € B}
Определение 4:
Декартовым произведением множеств А, В называют множество А х В, состоящее из всевозможных упорядоченных пар вида (а, b), где а € А, b € В: A*B = {(a,b):a € A, b € B}
Определение 5:
Разностью
множеств А, В называют множество А\В,
состоящее из всех элементов множества
А, не содержащихся в В: A\B
= {m:m
€ A
и m
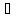 B}
B}
Вопрос 6. Отображения множеств. Свойства отображений.
Определение 1:
Пусть А, В — произвольные множества. Отображением множества А в множество В называют всякое правило f, по которому каждому элементу множества А сопоставляют вполне определенный (единственный) элемент множества В. Тот факт, что f есть отображение А в В, кратко записывают в виде: f: А->В.
Если при этом элементу а из A сопоставлен элемент Ь из В, то b называют образом элемента а, а а — прообразом элемента b при отображении f, что записывается в виде f(а) = b.
Определение 2:
Отображение f:A—>B называется сюръективным , если каждый элемент из В является образом хотя бы одного элемента из А, то есть f(A) = B.
Определение 3:
Отображение f:A—>B называется инъективным, если оно разные элементы множества А отображает в разные элементы множества В. Инъективные отображения называют также вложениями.
Определение 4:
Отображение f:A—>B называется биективным, или взаимно однозначным отображением А на, В, если оно сюръективно и инъективно.
Определение 5:
Отображение
f:
А —> В называется обратимым, если
существует такое отображение
 :
В —> А, что f
:
В —> А, что f = е,
= е,
 f=
е. При этом отображение
f=
е. При этом отображение
 называется обратным для f.
называется обратным для f.
Утверждение 1:
Отображение f:A—>B обратимо тогда и только тогда, когда оно биективно.
Определение 6:
Множества А и В называют равномощными, и пишут |А| = |B|, если существует биективное отображение f: А —> В.
Определение 7:
Множество
А называется конечным, если оно пусто
или равномощно отрезку
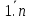 натурального ряда N. В последнем случае
число n
называют мощностью множества А, а само
А — n-элементным множеством. Мощность
пустого множества считается равной
нулю. Все остальные множества называются
бесконечными.
натурального ряда N. В последнем случае
число n
называют мощностью множества А, а само
А — n-элементным множеством. Мощность
пустого множества считается равной
нулю. Все остальные множества называются
бесконечными.
Утверждение 2:
Если А и В — конечные и равномощные множества, то для любого отображения f: А —► В эквивалентны условия:
а) f — сюръективно;
б) f — инъективно;
в) f — биективно.
Доказательство утверждения 2:
Из
определений видно что для доказательства
утверждения 2 достаточно установить
эквивалентность а) и б). Пусть f
— сюръективно, т. е. f(A) = В. Тогда |B|
= |f(A)| = | |
. Так как |
|
. Так как |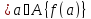 |
= 1 при любом а € A,
то равенство |
|
= 1 при любом а € A,
то равенство | |=
|А| возможно лишь в том случае, когда
f(a1)≠ f(a2)
при любых значениях a1.a2
€ А. Это означает, что f
— инъективно. Обратно, пусть f
— инъективно. Тогда оно разные элементы
отображает в разные, и поэтому |f{A)| = |
|=
|А| возможно лишь в том случае, когда
f(a1)≠ f(a2)
при любых значениях a1.a2
€ А. Это означает, что f
— инъективно. Обратно, пусть f
— инъективно. Тогда оно разные элементы
отображает в разные, и поэтому |f{A)| = | |
= |A|.Отсюда
и из условия |A|
= |B|
имеем: |f(A)| = |B|.
Теперь, учитывая включение f(A) c
В и конечность множества В, получаем:
f(A) = В. Следовательно, f
— сюръективно.
|
= |A|.Отсюда
и из условия |A|
= |B|
имеем: |f(A)| = |B|.
Теперь, учитывая включение f(A) c
В и конечность множества В, получаем:
f(A) = В. Следовательно, f
— сюръективно.
Доказано.
Свойства отображений:
Определение 8:
Композиций
отображений
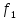 :В
—► С и
:В
—► С и
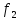 :A
—► Bназывается
отображение
:A
—► Bназывается
отображение
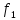 о
о
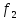 A
—► С, определенное условием (
A
—► С, определенное условием (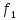 о
о
 )(a)
=
)(a)
=
 (
(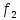 (a)). Для любого элемента a
€ А. То же самое отображение называют
еще произведением отображений
(a)). Для любого элемента a
€ А. То же самое отображение называют
еще произведением отображений
 и
и
 и
обозначают в виде
и
обозначают в виде
 .
Таким образом, (
.
Таким образом, ( )(a)
=
)(a)
=
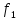 (
(
Утверждение 1:
Если
 :А
—► В,
:А
—► В,
 :B
—► C,
:B
—► C,
 :C
—► D,
то (
:C
—► D,
то (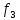 о
о
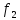 )
о
)
о
 =
=
 о (
о (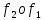 ).
).
Доказательство утверждения 1. Найдем образ элемента а из А при действии отображений,
записанных в левой и правой частях равенства:
((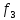 о
о
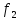 )
о
)
о
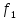 )(a)
= (
)(a)
= (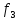 о
о
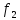 )(
)(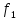 (а)) =
(а)) = (
( (
(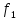 (а)))
(а)))
( )(a)
=
)(a)
=
 ((
(( )(a))
=
)(a))
=
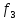 (
( (
( (a)))
(a)))
Утверждение 2:
Если
отображения
 :А
—► В,
:А
—► В,
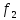 :В
—► C
сюръективны, инъективны или биективны,
то соответственно таким же будет и
отображение ¥ =
:В
—► C
сюръективны, инъективны или биективны,
то соответственно таким же будет и
отображение ¥ =
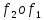 =
=
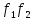 .
.
Доказательство
утверждения 2. Действительно, из
сюръективности
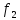 и
и
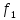 ,
следует соответственно для любого с €
С существует такой элемент b
€ В, что
,
следует соответственно для любого с €
С существует такой элемент b
€ В, что
 ,
и такой элемент а € А, что
,
и такой элемент а € А, что
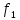 (a)
= b.
Отсюда имеем: ¥(a)
=
(a)
= b.
Отсюда имеем: ¥(a)
=
 (
(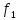 (a))
=
(a))
=
 (b)
= c,
и отображение ¥ - сюръективно. Если же
(b)
= c,
и отображение ¥ - сюръективно. Если же
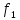 ,
, инъективны и а1 ≠ а2, то
инъективны и а1 ≠ а2, то
 ≠
≠
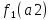 и
и
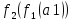 ≠
≠
 ,
¥(a1)
≠ ¥(a2),
¥ - инъективно. Заметим, что обратные
утверждения в общем случае неверны.
,
¥(a1)
≠ ¥(a2),
¥ - инъективно. Заметим, что обратные
утверждения в общем случае неверны.
Доказано.
