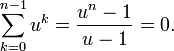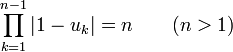- •Вопрос 1. Методы математических доказательств (метод непосредственной проверки, метод доказательства от противного, метод математической индукции).
- •2 Метод.
- •3 Метод.
- •Вопрос 2. Формула Бинома Ньютона.
- •Вопрос 3. Сочетания, размещения, перестановки. Теоремы о числе сочетаний, размещений и перестановок, их следствия.
- •Вопрос 4. Инверсии в перестановках. Чётные и нечётные перестановки при транспозиции.
- •Вопрос 5. Понятие множества. Основные операции на множествах. Свойства операций на множестве (ассоциативность, коммутативность, дистрибутивность). Декартово произведение множеств.
- •Вопрос 6. Отображения множеств. Свойства отображений.
- •Вопрос 7. Отношения на множестве, бинарные отношения. Отношения эквивалентности, отношения порядка.
- •Вопрос 8. Понятия группоида, полугруппы, группы и подгруппы. Совпадение нейтрального (единичного) и симметричного (обратного) элементов группы и подгруппы.
- •Вопрос 9. Подгруппа, порожденная подмножеством элементов группы.
- •Вопрос 10. Понятие наибольшего общего делителя (нод) и наименьшего общего кратного (нок) целых чисел. Условия существования и единственности нод. Взаимно простые числа и их свойства.
- •Вопрос 11. Алгоритм Евклида для целых чисел.
- •Вопрос 12. Представление нод двух чисел в виде их линейной комбинации:
- •Вопрос 13. Простые числа, их свойства. Основная теорема арифметики. Каноническое разложение целого числа.
- •Вопрос 14. Бесконечность множества простых чисел.
- •Вопрос 15. Понятие изоморфизма групп. Теорема о изоморфизме цикличных групп одного и того же порядка.
- •Вопрос 16. Критерий «быть подгруппой», следствия. Пересечение подгрупп.
- •Вопрос 17. Смежные классы. Теорема Лагранжа.
- •Вопрос18: Разложение подстановки в произведение независимых циклов. Цикловая структура подстановки.
- •Вопрос 19: Теоремы о гомоморфизме групп.
- •Вопрос 20. Обращение теоремы Лагранжа для циклических групп.
- •Вопрос 21. Классы сопряженных элементов, их свойства. Нормализатор элемента группы.
- •Вопрос 22. Группа биективных отображений множества (симметрическая группа). Определение группы подстановок. Сопряжённые элементы в симметрической группе.
- •Вопрос 23. Знакопеременная группа.
- •Вопрос 24. Циклические группы, их описание. Цикличность подгруппы циклической группы. Пример группы корней n-ой степени из единицы.
- •Вопрос 25. Порядок элемента конечной группы. Соотношения между порядком элемента и порядком группы.
Вопрос 21. Классы сопряженных элементов, их свойства. Нормализатор элемента группы.
Класс
сопряжённости элемента g
ϵ
G
есть множество
![]()
Свойства отношения сопряженности:
1)
Рефлективность.

2)
Симметричность. Если
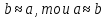 ,
т.к. из равенства
,
т.к. из равенства
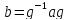 вытекает, что
вытекает, что
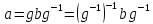 (если b
получается
трансформированием а элементом
(если b
получается
трансформированием а элементом
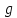 ,
то а получается трансформированием b
элементом
,
то а получается трансформированием b
элементом
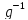 ).
).
3)
Транзитивность. Если
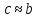 ,
то
,
то
 .
Действительно, из равенства
.
Действительно, из равенства
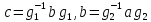 вытекает,
что
вытекает,
что
 (т.е. что элемент с получается
трансформированием а элементом
(т.е. что элемент с получается
трансформированием а элементом
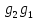 ).
).
4) Определяет разбиение группы G на непересекающиеся классы сопряженных между собой элементов.
5) Число классов сопряжённых элементов равно порядку группы. В некоммутативной группе число классов сопряжений меньше. Порядки сопряжённых между собой элементов одинаковы.
Нормализатор элемента группы:
Множество
всех элементов группы G, перестановочных
с данным элементом a
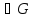 ,
является подгруппой группы G (нормализатором
элемента a), которая содержит цикличную
подгруппу, порождённую элементом a, в
качестве своего нормального делителя.
,
является подгруппой группы G (нормализатором
элемента a), которая содержит цикличную
подгруппу, порождённую элементом a, в
качестве своего нормального делителя.
Вопрос 22. Группа биективных отображений множества (симметрическая группа). Определение группы подстановок. Сопряжённые элементы в симметрической группе.
Группа подстановок:
Пусть π - подстановка, т.е. взаимно однозначное отображение множества {1,…,n} на себя.
Симметрическая группа:
Группу S(Ω) всех подстановок множества называют симметрической группой подстановок множества Ω.
В
случае , когда Ω = {1,…,n},
группу S(Ω)
называют симметрической группой
подстановок степени n
и обозначают через
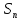 .
.
Сопряжённые элементы в симметрической группе:
Любые
две подстановки
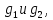 принадлежащие S, и имеющие одинаковую
цикловую структуры, сопряжены между
собой.
принадлежащие S, и имеющие одинаковую
цикловую структуры, сопряжены между
собой.
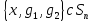

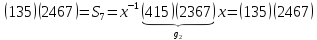
(135)(2467)
(415)(2367)
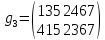
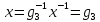
Вопрос 23. Знакопеременная группа.
Знакопеременной группой подстановок степени n (обозн. An) называется подгруппа симметрической группы Sn степени n, содержащая только чётные подстановки.
Знакопеременная группа является нормальной подгруппой симметрической группы.
Порядок знакопеременной группы равен: | An | = n! / 2.
Вопрос 24. Циклические группы, их описание. Цикличность подгруппы циклической группы. Пример группы корней n-ой степени из единицы.
Группа (G,·) называется циклической , если она порождена одним элементом a, то есть все её элементы являются степенями a (или, если использовать аддитивную терминологию, представимы в виде na, где n — целое число.)
Таким
образом, мы называем G
циклической, если G
= {an|
![]() }.
Иначе говоря, группа G
циклическая, если в G
любая подгруппа, содержащая a,
совпадает с G.
Это следует из того, что в такой подгруппе
должны содержаться все степени элемента
a.
}.
Иначе говоря, группа G
циклическая, если в G
любая подгруппа, содержащая a,
совпадает с G.
Это следует из того, что в такой подгруппе
должны содержаться все степени элемента
a.
Каждая подгруппа G циклична.
Корни из единицы образуют по умножению группу. Обратный элемент для каждого элемента этой группы совпадает с сопряжённым ему. В частности, любая целая степень корня из единицы тоже является корнем из единицы.
Группа
корней из единицы изоморфна аддитивной
группе классов вычетов
![]() .
Отсюда следует, что она является
циклической группой; в качестве
порождающего (первообразного) можно
взять любой элемент uk,
индекс k
которого взаимно прост с n.
.
Отсюда следует, что она является
циклической группой; в качестве
порождающего (первообразного) можно
взять любой элемент uk,
индекс k
которого взаимно прост с n.
Следствия:
элемент u1 всегда является первообразным;
если
n —
простое число, то степени любого корня,
кроме
![]() ,
охватывают всю группу;
,
охватывают всю группу;
число
первообразных корней равно
![]() ,
где
,
где
![]() —
функция Эйлера.
—
функция Эйлера.
Если n > 1, то для суммы степеней любого первообразного корня из единицы u имеет место формула: