Вопрос 3. Сочетания, размещения, перестановки. Теоремы о числе сочетаний, размещений и перестановок, их следствия.

Определение 1:

Размещением из n элементов множества А = {a1,...,an} по m называется любой упорядоченный набор m различных элементов множества А.

Определение 2:

Любой упорядоченный набор всех n элементов множества A, взятых по одному разу, называется перестановкой элементов множества А.

Определение 3:

Сочетанием из n элементов множества А = {a1,...,an} пo m называется любое m-элементное подмножество множества А.

Теорема:

Введем следующие обозначения:

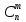-- число различных сочетаний из n no m,

– число различных размещений из n по m.

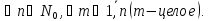Верны формулы:

Сочетаний =

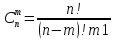Размещение = n(n-1)…(n-m+1)

Перестановки P_n= n!

Доказательство:

Укажем путь построения всех размещений по m элементов из множества |А|=n .Каждое такое размещение имеет вид:

(a1,а2,…..,аm),где а1,а2,…,аm – различные числа из А.

При построении размещения в качестве а1 можно взять любое число из множества А.Следовательно, число различных вариантов выбора а1 равно n.Если первый элемент размещения уже выбран, то в качестве 2-ого можно взять любое число, отличное от первого. Следовательно, при любом первом элементе второй можно выбрать в n-1 вариантах. Значит, указанным образом упорядоченных пар вида а1,а2 можно построить n(n-1) штук. Аналогично, при любых выбранных а1,а2 в качестве а3 можно взять любое из n-2 оставшихся чисел. Следовательно, упорядоченных троек вида а1,а2,а3 можно составить n(n-1)(n-2). Продолжая этот процесс, мы построим n(n-1)…(n-m+1) размещений. Легко видеть, что все построенные размещения различны и любое размещение из n по m будет таким образом построено. Формула для перестановок получается в частном случае, когда m=n. Докажем формулу для сочетаний. Возьмем произвольное сочетание (а1,а2,…аm). Переставляя всевозможным образом его элементы, мы получим формулу = m!. Следовательно, мы получили m! различных размещений из n по m. Отсюда видно, что число различных размещений из n по m в m! Раз больше числа сочетаний из n по m. Следовательно,

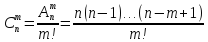
Доказано.

Следствие 1:

Следствие 2:

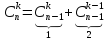
Вопрос 4. Инверсии в перестановках. Чётные и нечётные перестановки при транспозиции.

Определение 1:

Говорят, что числа 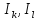в перестановке s = () образуют инверсию (или беспорядок), если большее из них расположено левее меньшего, т. е. 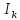> 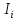и i < к.

Определение 2:

Перестановку называют четной, если она содержит четное число инверсий, и нечетной в противном случае.

Примеры:

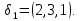
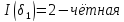
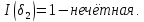
Определение 3:

Преобразование перестановки, заключающееся в перемене местами каких-либо двух ее элементов, называется транспозицией.

Теорема 1:

Если перестановка s1 получена из перестановки s с помощью одной транспозиции, то s и s1 являются перестановками разной четности.

Теорема 2:

Кол-во чётных и нечётных перестановок n-элементов одинаково.

Теорема 3:

Количество всех перестановок

Доказательство теоремы 1:

1часть. Рассмотрим случай 2 соседних элементов. При ней их расположение по отношению к другим элементам не меняется.

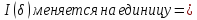чётность меняется. (инверсия либо добавилась либо вычлась).

2часть. Общий случай.

Транспозиция элементов α и β между которыми стоят k элементов

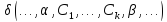
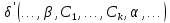
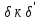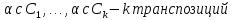
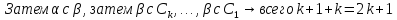Переход от можно совершить путём транспозиции соседних элементов:

– транспозиций соседних элементов.

Согласно части 1 на каждом шаге чётность меняется. В итоге она изменяется (2k+1) раз т.е. в результате чётности поменялись.

Доказательство Теоремы 2:

Обозначим через P число всех чётных перестановок n элементов, через q - число всех нечётных. Покажем, что p=q.

В каждой чётной перестановке поменяем местами 1-ый и 2-ой элементы. В результате получим p различных нечётных перестановок. А всего нечётных q, то есть p≥q. В этом рассуждении можно поменять местами чётные и нечётные перестановки, тогда q≤p, а значит p=q.

Следствие: Число чётных и нечётных перестановок равно (одинаково)=.