Вопрос 9. Подгруппа, порожденная подмножеством элементов группы.

Пусть M - подмножество группы G, тогда символом (М) будем обозначать пересечение всех подгрупп, содержащих множество M. Это множество - подгруппа, порожденная множеством М: (М)= . Множество (М) состоит в точности из тех элементов, которые можно записать через элементы из М, используя операции умножения и взятия обратного элемента . Говорят, что М порождает подгруппу Н, если (М)=Н.

Вопрос 10. Понятие наибольшего общего делителя (нод) и наименьшего общего кратного (нок) целых чисел. Условия существования и единственности нод. Взаимно простые числа и их свойства.

Наибольшим общим делителем (НОД) для двух целых чисел m и n называется наибольший из их общих делителей. (НОД(m, n))

Наибольший общий делитель существует и однозначно определён, если хотя бы одно из чисел m или n не ноль.

Наименьшее общее кратное (НОК) двух целых чисел m и n есть наименьшее натуральное число, которое делится на m и n. (НОК(m, n))

Целые числа называются взаимно простыми, если они не имеют никаких общих делителей, кроме ±1.

Свойства:

-Числа a и b взаимно просты тогда и только тогда, когда выполняется одно из эквивалентных условий.

-Наибольший общий делитель a, b равен единице.

-Существуют целые x и y такие, что ax+by=1 (соотношение Безу).

-Любые два (различных) простых числа взаимно просты.

-Если a — делитель произведения bc, и a взаимно просто с b, то a — делитель c.

-Если числа a₁,…, a_n — попарно взаимно простые числа, то НОК(a₁,…, a_n) = |a₁·…·a_n|. Например, НОК(9,11)=9*11=99

Вопрос 11. Алгоритм Евклида для целых чисел.

Вариант 1:

Пусть a и b — целые числа, не равные одновременно нулю, и последовательность чисел определена тем, что каждое r_k — это остаток от деления предпредыдущего числа на предыдущее, а предпоследнее делится на последнее нацело, то есть

a = bq₀ + r₁

b = r₁q₁ + r₂

r₁ = r₂q₂ + r₃

r_{k − 2} = r_{k − 1}q_{k − 1} + r_k

r_{n − 1} = r_nq_n

Тогда НОД(a,b), наибольший общий делитель a и b, равен r_n, последнему ненулевому члену этой последовательности.

Существование таких r₁,r₂,..., то есть возможность деления с остатком m на n для любого целого m и целого , доказывается индукцией по m.

Корректность этого алгоритма вытекает из следующих двух утверждений:

1) Пусть a = bq + r, тогда НОД (a, b) = НОД (b, r).

Доказательство :

1. Пусть k — любой общий делитель чисел a и b, не обязательно максимальный, тогда a = t₁ * k ; b = t₂ * k; где t₁ и t₂ — целые числа из определения.

2. Тогда k также общий делитель чисел b и r, так как b делится на k по определению, а r = a − bq = (t₁ − t₂ * q) * k (выражение в скобках есть целое число, следовательно, k делит r без остатка)

3. Обратное также верно и доказывается аналогично пункту 2 - любой делитель b и r так же является делителем a и b.

4. Следовательно, все общие делители пар чисел a,b и b,r совпадают. Другими словами, нет общего делителя у чисел a,b, который не был бы также делителем b,r, и наоборот.

5. В частности, максимальный делитель остается тем же самым. Что и требовалось доказать.

2) НОД(0,r) = r для любого ненулевого r (т.к. 0 делится на любое целое число, кроме нуля).

Проще сформулировать алгоритм Евклида так: если даны натуральные числа a и b и, пока получается положительное число, по очереди вычитать из большего меньшее, то в результате получится НОД.

Вариант 2:

Содержание алгоритма Евклида сводится к последовательному вычислению следующих равенств:

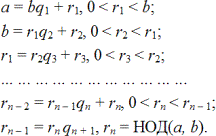
Действие алгоритма прекращается тогда, когда полученный остаток равен нулю; последний ненулевой остаток (r_n) равен наибольшему общему делителю.