Вопрос 7. Отношения на множестве, бинарные отношения. Отношения эквивалентности, отношения порядка.

Определение 1:

Бинарным отношением на множестве А называют любое подмножество р множества (т. е. декартова квадрата множества А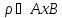 ). По аналогии с этим, n-арным отношением на множестве А называют любое подмножество множества 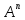. Если р — отношение на А и (а, b) € р, то говорят, что элемент а находится в отношении р к элементу b. Этот факт записывают также в

виде apb.

Определение 2:

Отношение р на множестве А называется:

1) рефлексивным, если Va € А : {ара),

2) симметричным, если Va, b € А : (apb => bра),

3) транзитивным, если Va, b, с € A : (арb, bрс => арc),

4) антисимметричными, если Va, b € А : (apb, bpa => a = b).

Пример:

Отношение делимости и отношение " ≤ " на множестве N рефлексивны, антисимметричны и транзитивны. Отношение параллельности прямых симметрично и транзитивно.

Определение 3:

Бинарное отношение р на множестве А называется отношением эквивалентности, если оно рефлексивно, симметрично и транзитивно. При этом элементы, находящиеся в отношении р,

называют эквивалентными (точнее, р-эквивалентными).

Теорема 1:

Если р — отношение эквивалентности на множестве А, то А распадается на непересекающиеся подмножества так, что для любых а,Ь € А : а,Ь содержатся в одном подмножестве в том и только том случае, когда apb.

Доказательство:

Обозначим через подмножество элементов из А, эквивалентных а, т. е. 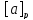= {x∊ A : xpa},

и докажем, что A = 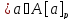и Va, b € А: (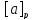 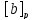= пусто множество или ).

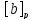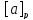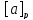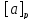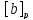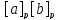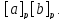Из определений, что а ∊ и поэтому каждое из множеств не пусто и каждый элемент из А содержится хотя бы в одном из таких подмножеств. Остается доказать, что любые два подмножества и либо совпадают , либо не пересекаются. Пусть пересекаются , и x ∊ Тогда имеем соотношения: apx и bpx. Из них, используя свойства симметричности и транзитивности , получим xpa и bpa. Если с- любой элемент из 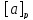, то имеем apc, что вместе с bpa приводит к соотношению bpc. 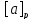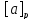Следовательно, с ∊ т.е.С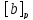 . Аналогично доказывается и обратное включение. 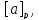Таким образом, из наличия во множествах 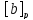одного общего элемента x следует их полное совпадение. Значит, различные подмножества типа 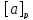либо совпадают, либо не пересекаются. Доказано.

Определение 4:

Бинарное отношение на множестве А называется отношением частичного порядка, если оно рефлексивно, транзитивно и антисимметрично. Множество с заданным на нем отношением частичного порядка называют частично упорядоченным.

Вопрос 8. Понятия группоида, полугруппы, группы и подгруппы. Совпадение нейтрального (единичного) и симметричного (обратного) элементов группы и подгруппы.

Группоид:

Множество с заданной на нём одной бинарной операцией.

Группа:

Непустое множество G с заданной на нём бинарной операцией называется группой (G, * ), если выполнены следующие аксиомы:

- ассоциативность: ;

- наличие нейтрального элемента: ;

- наличие обратного элемента:

Полугруппа:

Непустое множество S с заданной на нём ассоциативной операцией.

Подгруппа:

Непустое подмножество H группы G, если оно само является группой относительно той же операции.

Совпадение нейтрального (единичного) и симметричного (обратного) элементов группы и подгруппы:

Если Н — подгруппа группы (G, ), то ее нейтральный элемент 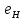совпадает с 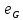и для каждого h 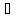Н

обратный к h элемент в Н совпадает с обратным к h элементом в G.

Доказательство:

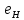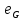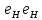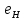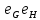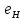Равенство = следует из равенств =и = ввиду теоремы (для любых g,h € H каждое из уравнений g*x = h и у*g = h однозначно разрешимо в H).

Последняя часть утверждения теперь следует из единственности решения в G уравнения hx = .
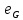