
- •«Курский государственный университет»
- •Кафедра технической графики
- •Примеры и решение задач по технической механике
- •Что такое "сопротивление материалов"
- •Классификация внешних сил и опор
- •Допущения в сопромате
- •Метод сечений
- •Напряжения
- •Растяжение и сжатие
- •Деформации
- •Напряжённое состояние
- •Запас прочности
- •Статически неопределимые системы
- •Задачи на растяжение (сжатие)
- •Чистый сдвиг
- •Практические расчеты на срез и смятие
- •Неразъемные соединения
- •Заклёпочные соединения
- •Сварные соединения
- •Напряжения и перемещения при кручении бруса круглого поперечного сечения
- •Геометрические характеристики плоских сечений
- •Задачи на кручение и сдвиг (срез и смятие)
- •Прямой изгиб
- •Поперечные силы и изгибающие моменты
- •Дифференциальные зависимости между распределёнными нагрузками, поперечной силой и изгибающим моментом
- •Общие указания к построению эпюр
- •Нормальные напряжения при изгибе
- •Касательные напряжения при прямом поперечном изгибе
- •Перемещения при изгибе
- •Задачи на изгиб
Задачи на растяжение (сжатие)
Рассмотрим примеры, связанные с деформациями растяжения (сжатия), в которых определяются величины, связанные с нагружением, деформированием и построением эпюр, характеризующих процесс.
Пример 1.
ℓ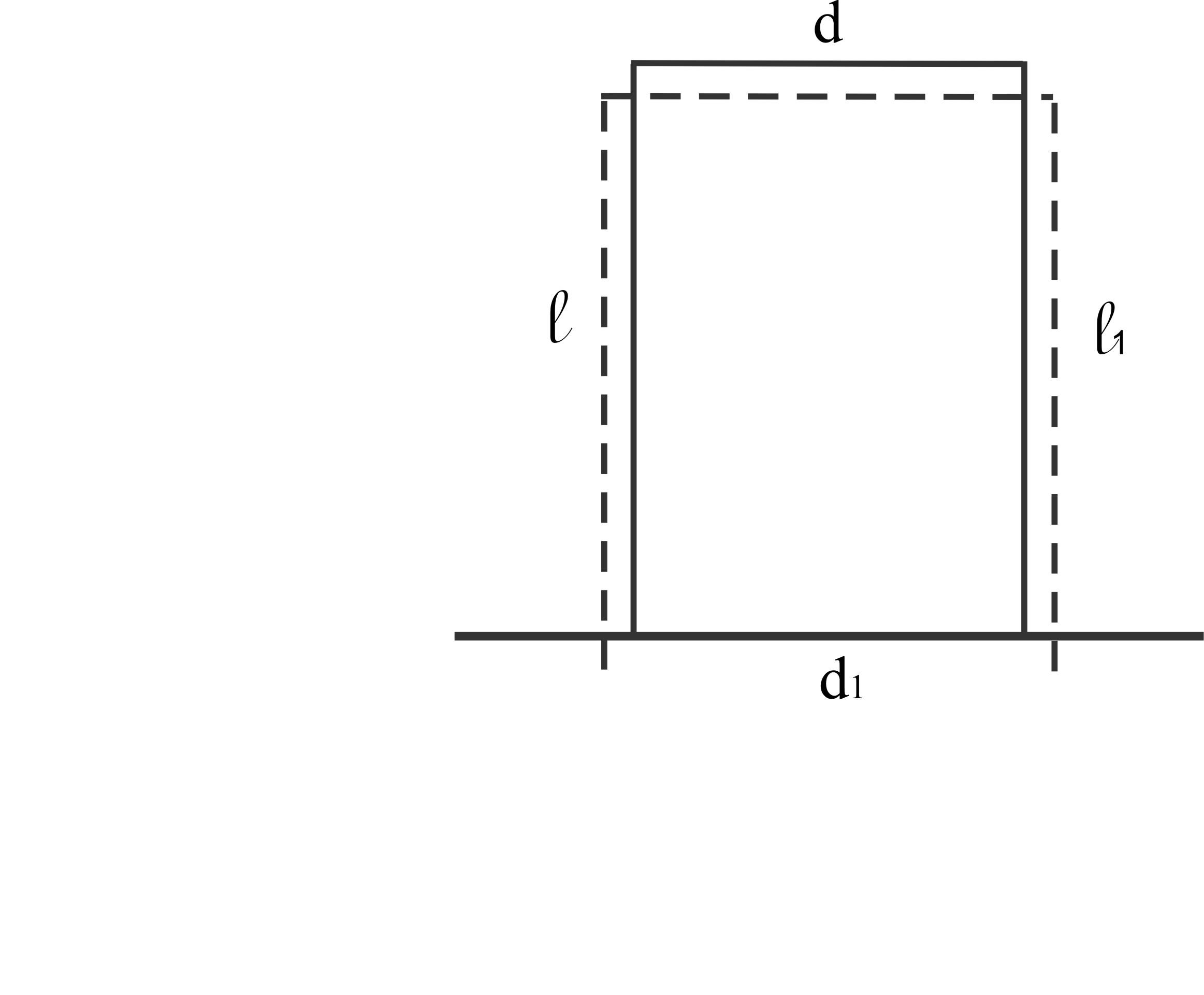 =
100 мм; ℓ1 =
99,9 мм
=
100 мм; ℓ1 =
99,9 мм
d = 40 мм; d1 = 40,01 мм
Найти коэффициент Пуассона.
Решение:
│ε│
=
![]() ,
│ε'│ =
,
│ε'│ =
![]()
μ
(ν) =
![]() =
=
![]() = 0,25.
= 0,25.
Пример 2.
Подкос ВС квадратного сечения - дуб
[σ] = 12 МПа, а = 1м, F = 10 кН
Определить размер подкоса.
Решение:
R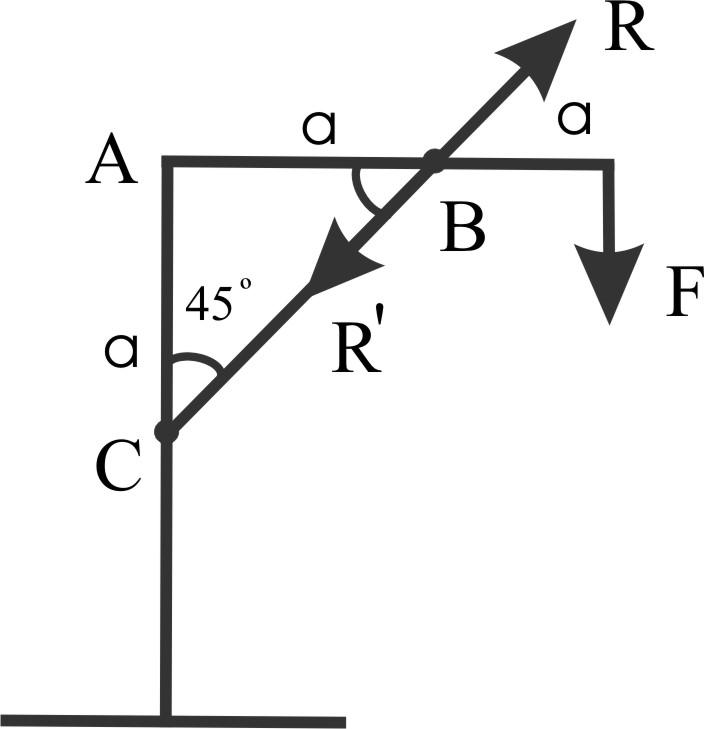 вдоль стержня, подкос испытывает сжатие.
вдоль стержня, подкос испытывает сжатие.
Условие равновесия определим:
сумма моментов относительно А
Σ MA = с = - F 2a + R sin45ºa,
откуда
R
=
![]() =
=
![]() = 28,4 кН
= 28,4 кН
Для сжатия расчетное соотношение:
A
=
![]() =
=
![]() = 2,3710-3
м2
= 2,3710-3
м2
т.к.
квадрат, то B
=
![]()
в
=
![]() ×10-3
м = 48,6 мм.
×10-3
м = 48,6 мм.
Пример 3.
Стальная полоса 30×10 мм, ℓ = 250 мм растянута силой P = 60 кН;
Е = 2×105 МПа.
Вычислить: σ (нормальное напряжение); ∆ℓ (абсолютное удлинение);
ε (относительное удлинение).
Решение:
σ
=
![]() =
=
![]() = 2
= 2![]() 108
Па = 200 МПа
108
Па = 200 МПа
По закону Гука
ε
=
![]() =
=
![]()
![]()
![]() =
=
![]() =
=
![]() = 10-3
= 10-3
εℓ
= ∆ℓ =
![]() =
=
![]()
![]() ℓ
= 10-3×250
мм = 0,25 мм.
ℓ
= 10-3×250
мм = 0,25 мм.
Пример 4.
Цилиндрический стальной стержень ℓ = 40 см и D = 2 см в средней части ослаблен прорезью ℓ1 = 20 см и шириной h = 1 см, растянут силой P = 15 кН, E = 2×105 МПа.
Вычислить: Δℓ полное; σ ослабл и σ неосл.
Решение:
Изобразим условие:
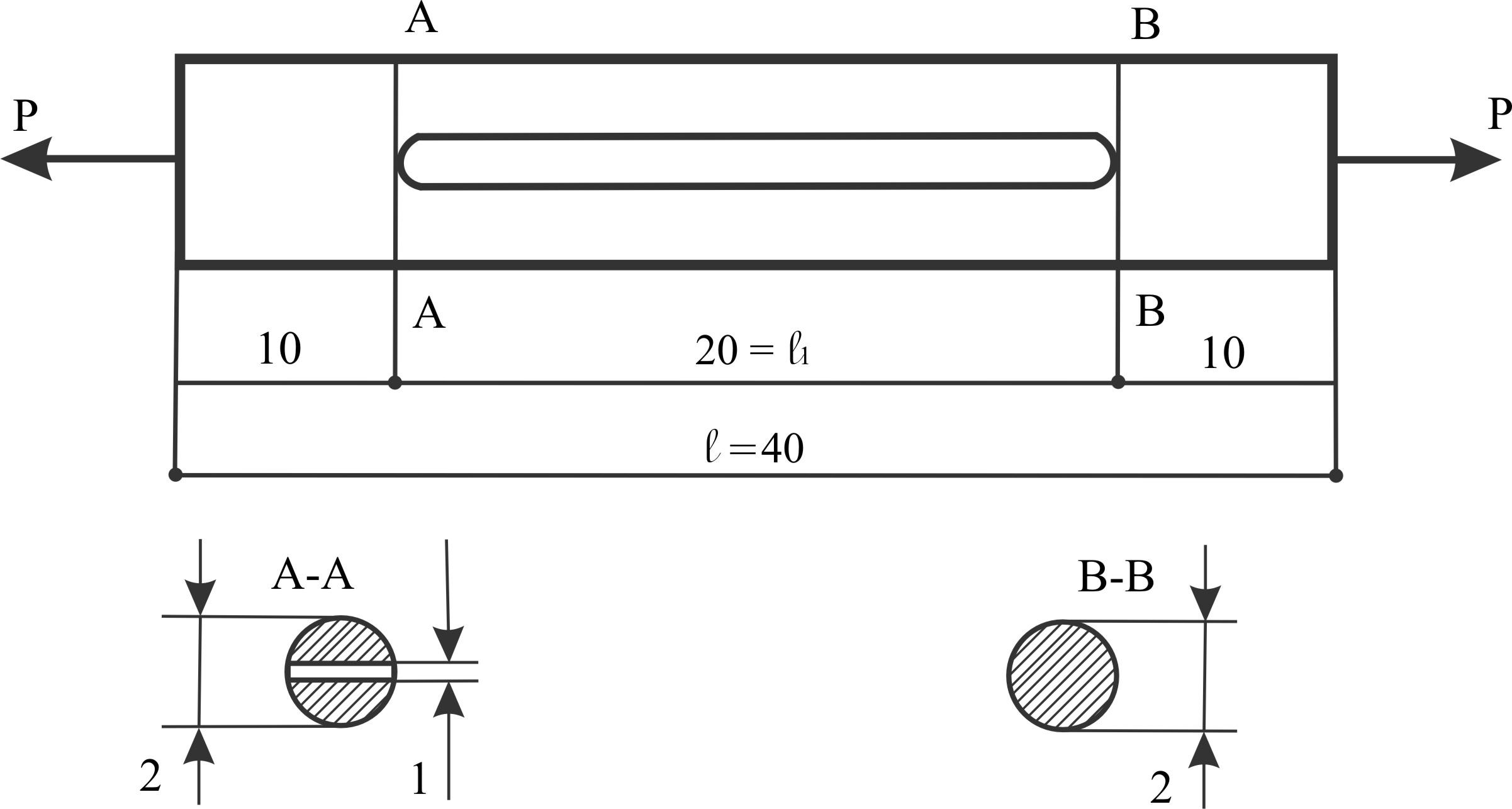
В неослабленных местах (без прорези)
σ1
=
![]() =
=
![]() =
=
![]() Па = 4,77×107
Па = 47,7 МПа.
Па = 4,77×107
Па = 47,7 МПа.
∆ℓ1
=
![]()
![]() (ℓ
- ℓ1)
=
(ℓ
- ℓ1)
=
![]() = 4,77
= 4,77![]() 10-5
м = 0,0477 мм.
10-5
м = 0,0477 мм.
В
ослабленной части (с прорезью) F2
=
![]() - Dh.
- Dh.
σ2
=
![]() =
=
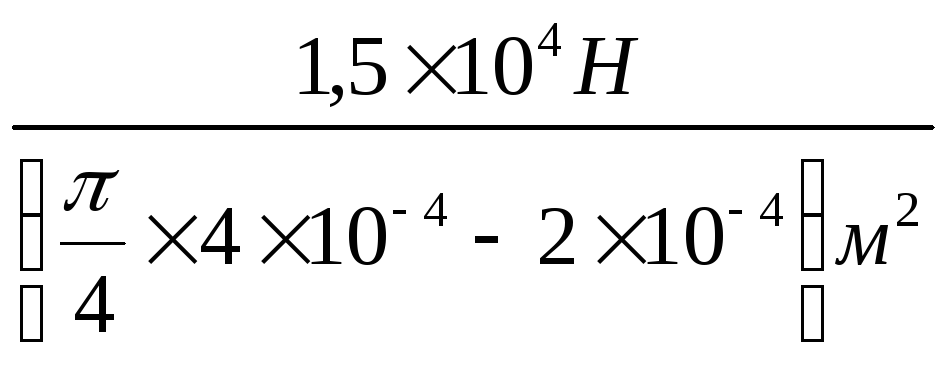 = 1,31
= 1,31![]() 108
Па = 131 МПа.
108
Па = 131 МПа.
∆ℓ2
=
![]()
![]() ℓ1
=
ℓ1
=
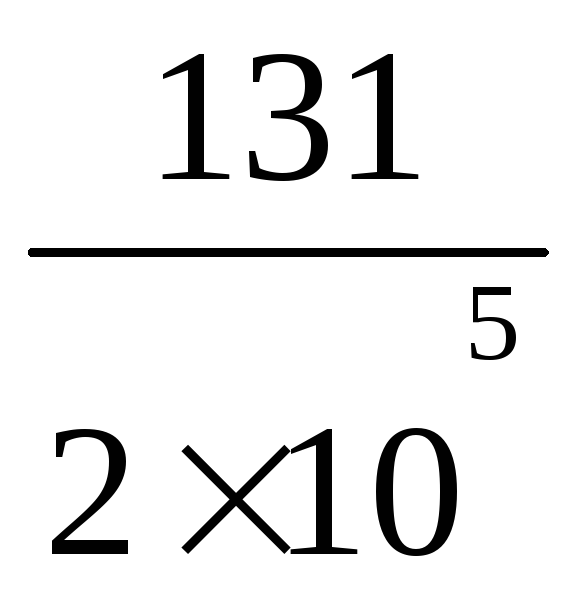
![]() 2
2![]() 10-1
= 131
10-1
= 131![]() 10-6м
= 0,131 мм.
10-6м
= 0,131 мм.
∆ℓ = ∆ℓ1 + ∆ℓ2 = 0,1787 мм = 0,18 мм.
Пример 5.
Мачтовый
кран АВ (труба) 20![]() 18
мм;
18
мм;
С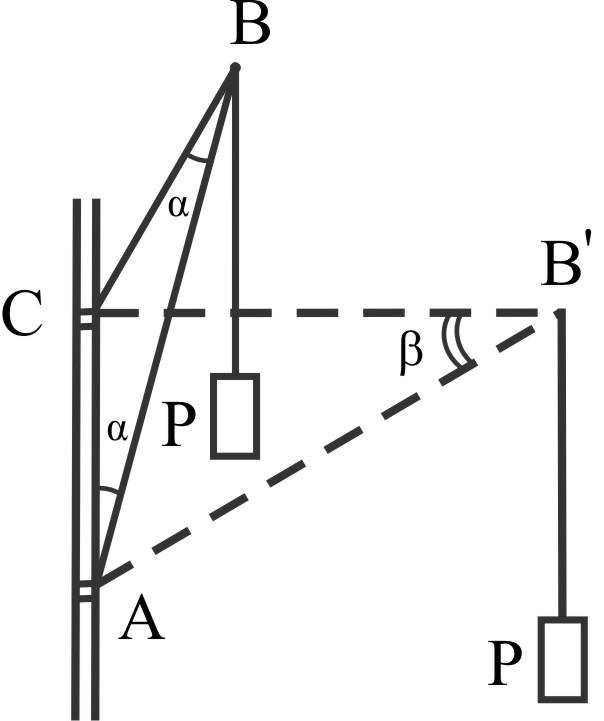 В
(трос) FCB
= 0,1 см2
В
(трос) FCB
= 0,1 см2
P = 2кН; α = 15º; β = 30º
∆ABC → ∆AB'C
Вычислить σAB и σBC.
Найти - как изменятся напряжения при переводе крана из ABC в AB'C
Решение:
Для разложения P = (NAB; NBC) используем теорему синусов
I.
![]()
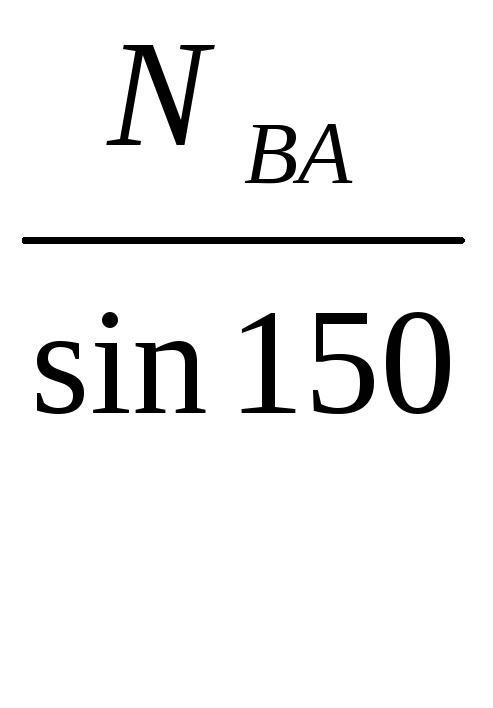 =
=
![]() =
=
![]() ; NBC
= P;
; NBC
= P;
NBA
=
![]() = -
= -
![]() = - 1,93 P.
= - 1,93 P.
σBA
=
![]() = -
= -
![]() = -6,47
= -6,47![]() 107
Па = - 64,7 МПа.
107
Па = - 64,7 МПа.
σBC
=
![]() =
=
![]() = 200 МПа.
= 200 МПа.
II. после перевода в новое положение
![]()
![]() =
=
![]() =
=
![]() ,
что дает
,
что дает
NB'A
= 2P,
σB'A
=
![]() = 67,2 МПа.
= 67,2 МПа.
NB'C
=
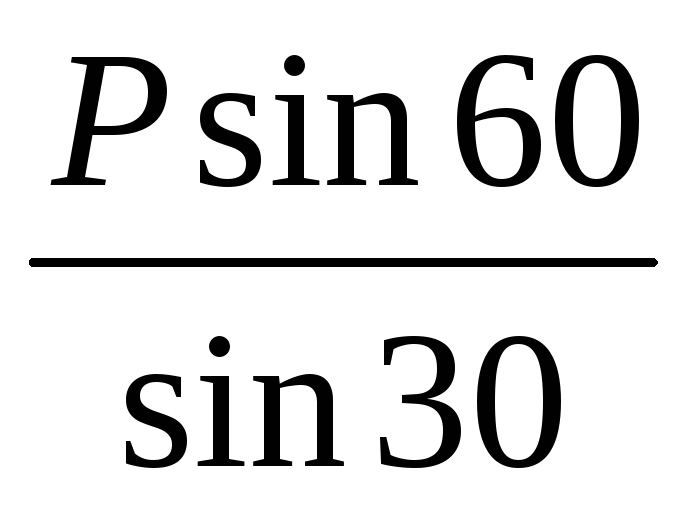 = 2P
= 2P![]() 0,866;
σB'C
= 346,4 МПа.
0,866;
σB'C
= 346,4 МПа.
Пример 6.
Ступенчатый брус.
Указаны силы и сечения на рисунке.
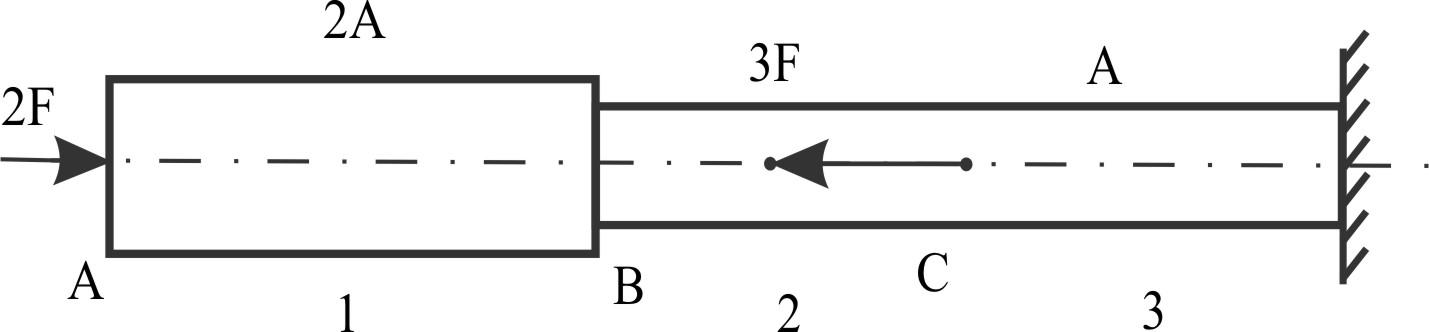
Построить эпюры сил и напряжений.
Решение:
Строим от свободного конца: в "C"; скачок N, σ меняется в "B" за счет изменения сечения; в "C" за счет скачка силы.
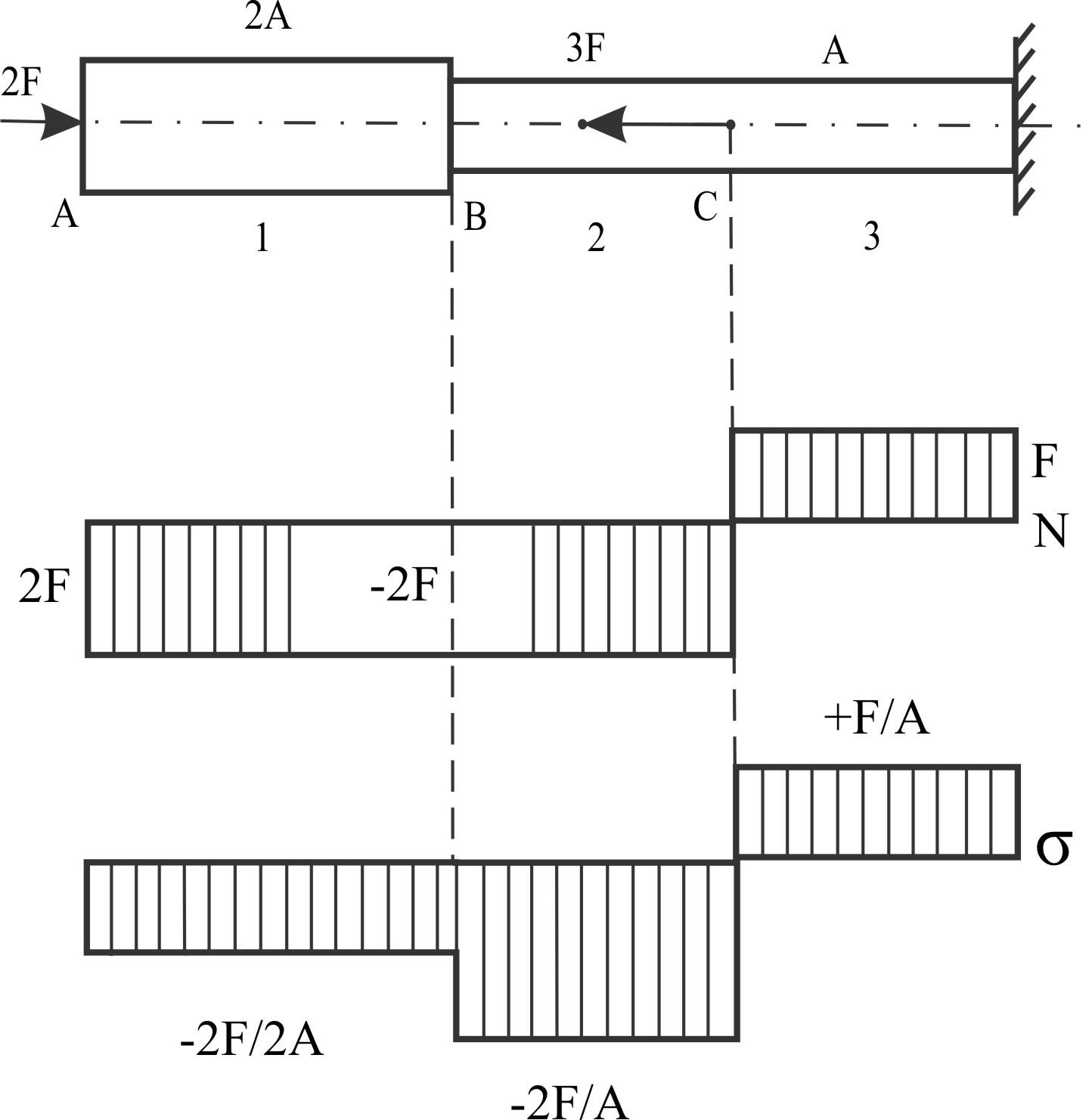
Пример 7.
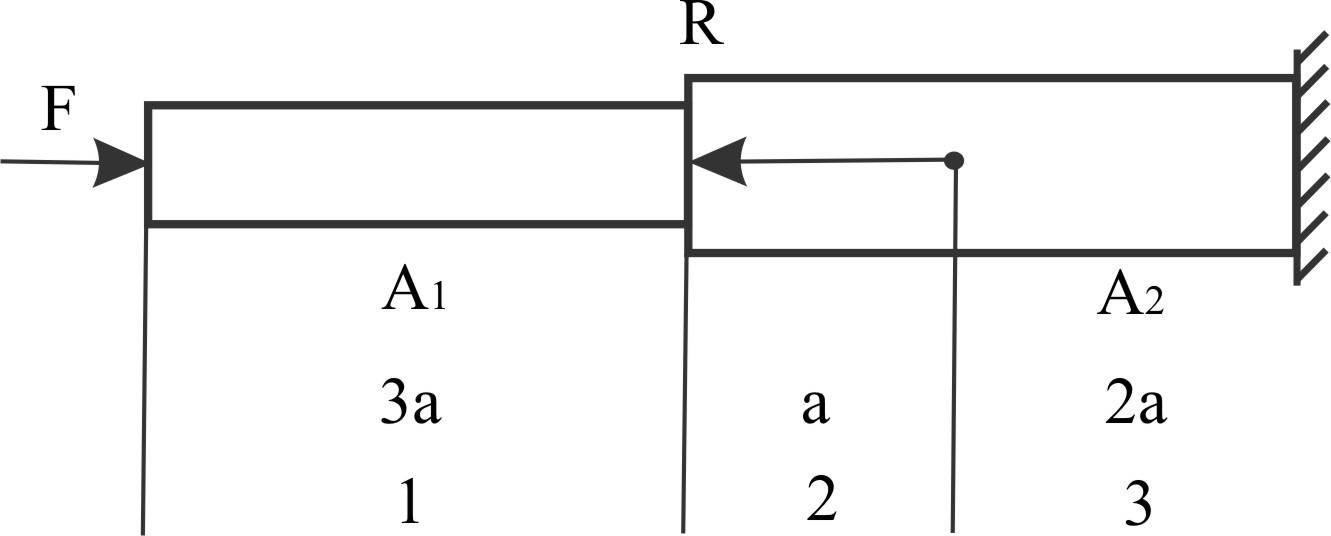
F = 40 кН, R = 60 кН
A1 = 800 мм2, A2 = 1600 мм2
a = 0,2 м, E = 2×1011 Па
Определить изменения длин участков и перемещение свободного конца.
Решение:
|
∆ℓ1
=
|
N1 = -F |
∆ℓ1 = - 0,15 мм |
|
∆ℓ2
=
|
N2 = -F |
∆ℓ2 = - 0,025 мм |
|
∆ℓ3
=
|
N3 = R - F |
∆ℓ3 = + 0,025 мм |
λ = ∆ℓ1 + ∆ℓ2 + ∆ℓ3 = - 0,15 мм.
Весь брус укоротится, укорочение определится перемещением свободного конца.
Пример 8.
E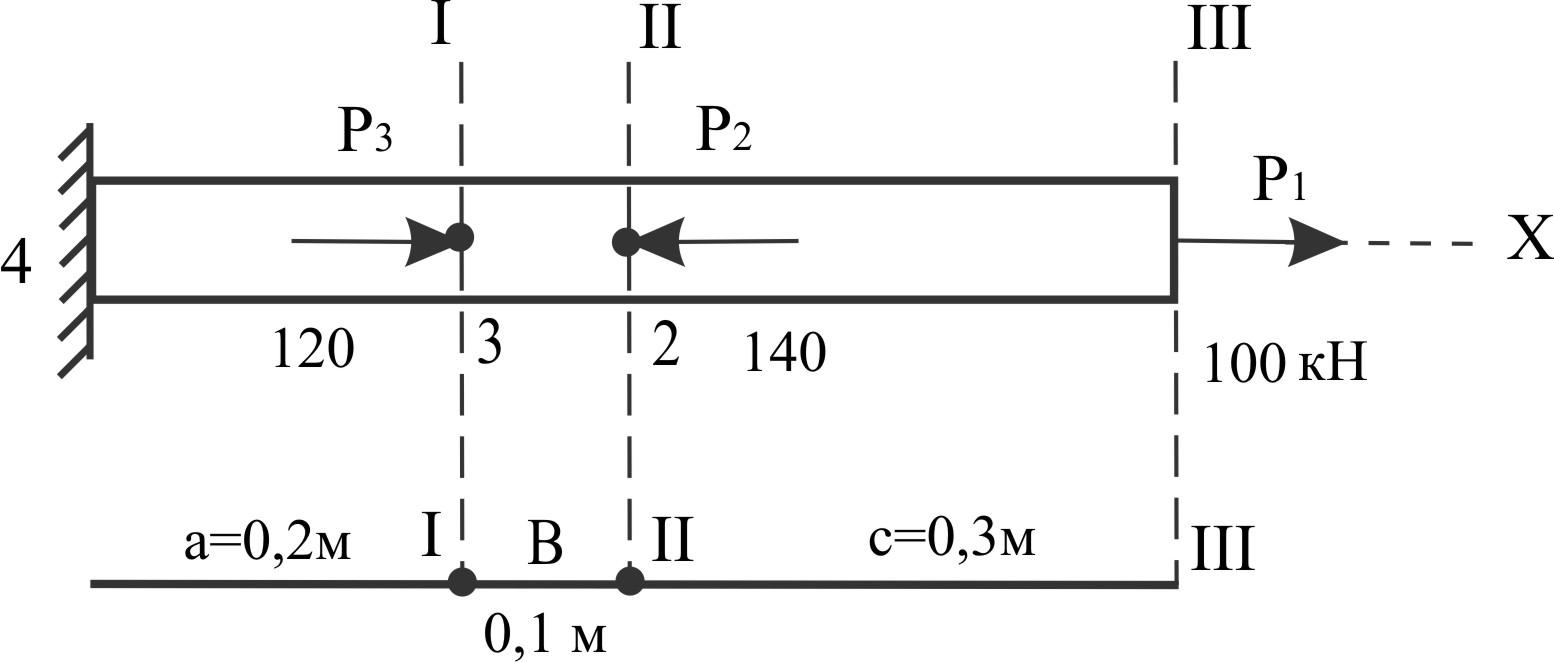 = 2×105
МПа
= 2×105
МПа
Ø = 3 см
P1 = 100 кН
P2 = 140 кН
P3 = 120 кН
Вычислить продольные силы N и σ на участках 1-2, 2-3, 3-4; перемещения ω сечений I-I, II-II и III-III; построить эпюры N, σ, ω.
Решение:
Продольные силы на участках (начиная от свободного конца) на отдельных участках = Σ всех сил по одну сторону от сечения.
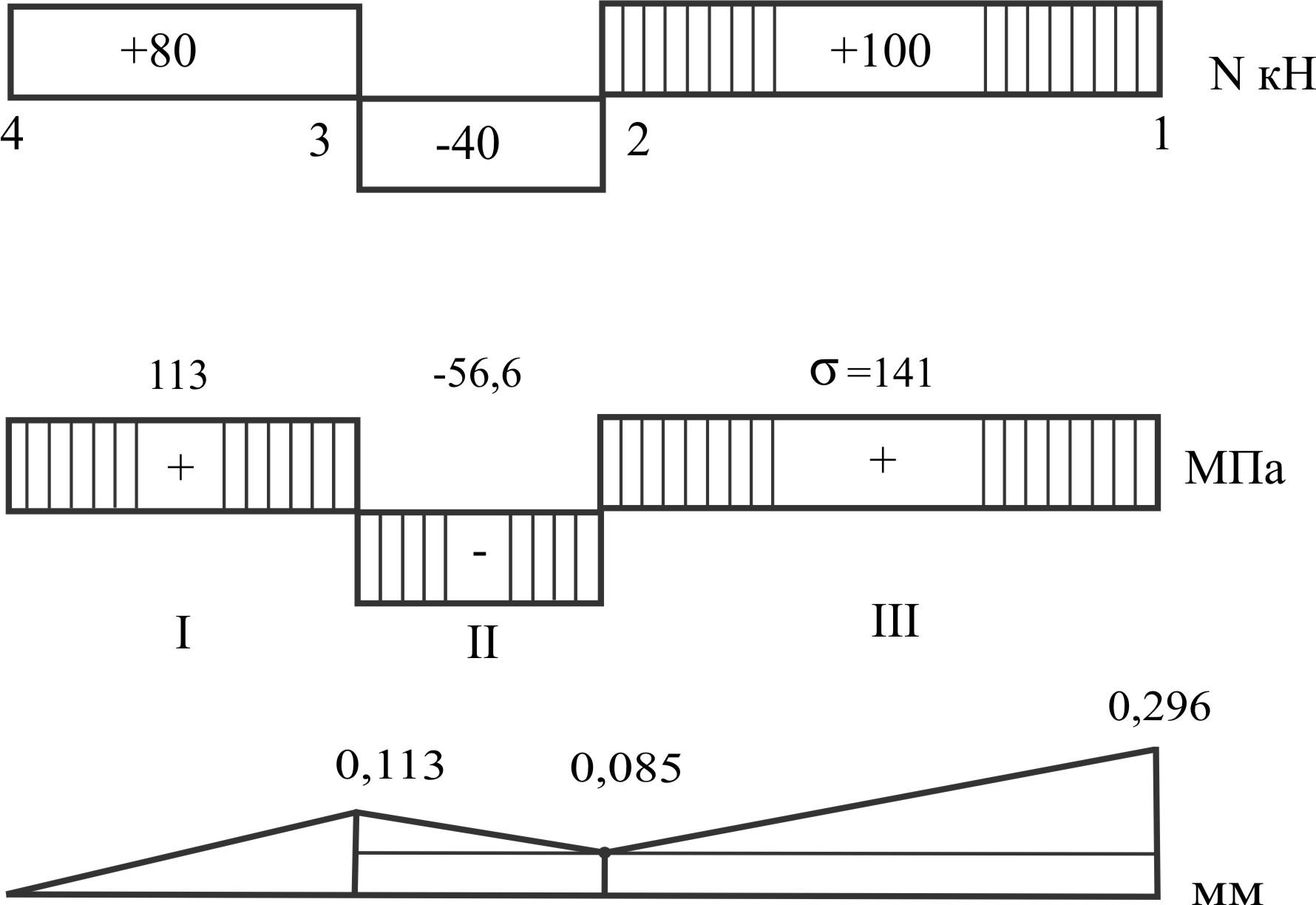
σ
=
![]() .
.
F
=
![]() D2.
D2.
∆ℓi
= ωi
=
![]() ℓi.
ℓi.
ω = Σ ωi.
∆ℓ1 = ω1 = 0,113,
∆ℓ2 = - 0,028, ω2 = 0,085,
∆ℓ3 = 0,211, ω3 = 0,296.
Пример 9.
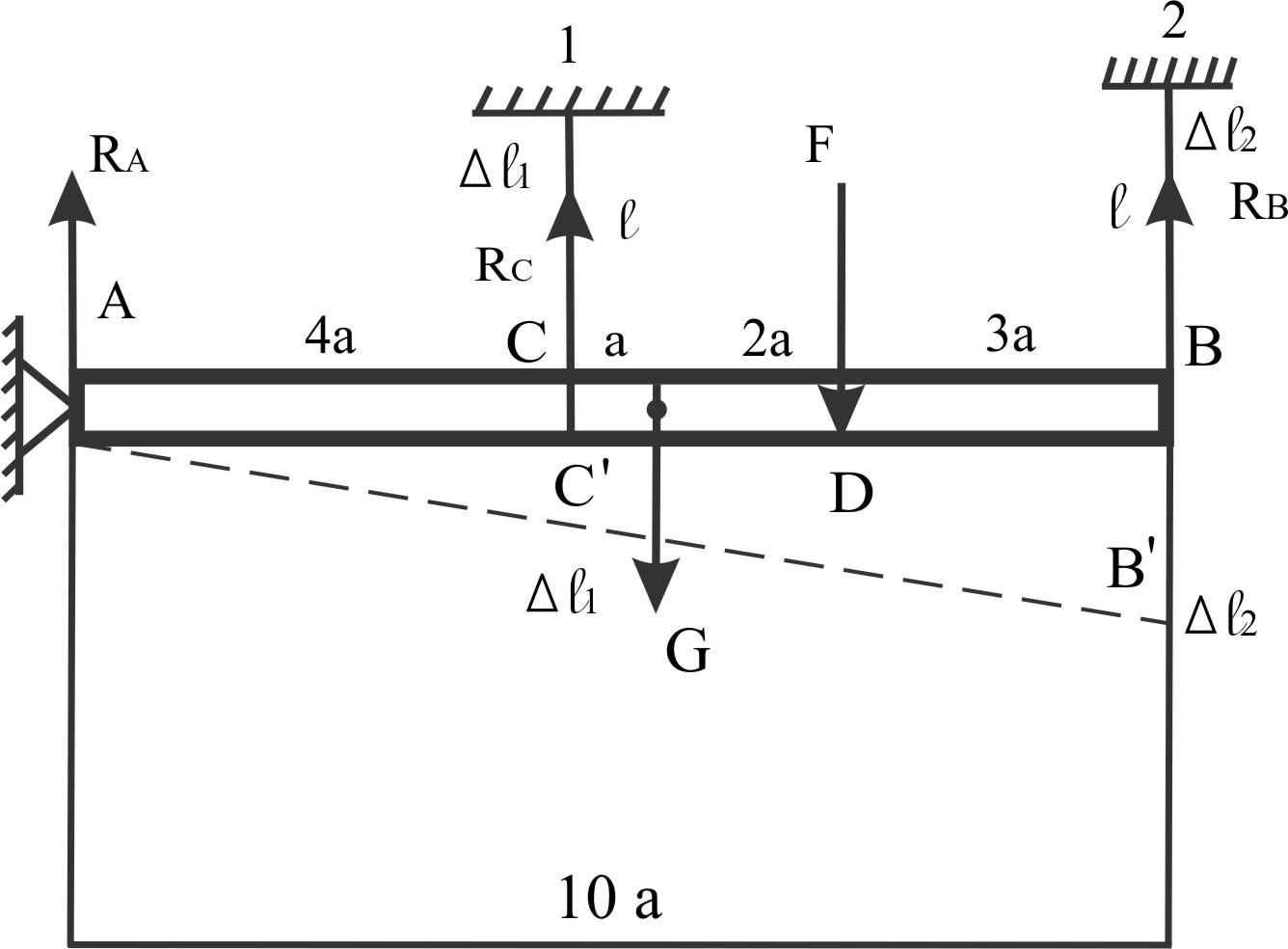
Абсолютно жесткая балка
В "С" и "В" подвес на стержнях
ℓ = 2 м; в "D" - F = 20 кН;
сечение А1 = 3 см2; А2 = 6 см2
E = 2×105 МПа
Gбалки = 40 кН
Определить σ1 и σ2 (напряжения в стержнях подвеса).
Решение:
Введя реакции RA; RC и RB имеем 3 неизвестных, уравнений равновесия 2 (для сил и моментов), значит задача статически неопределима, следовательно необходимо использовать геометрическое уравнение для перемещений
∆ ACC' ~ ∆ ABB', ε1 = ε2.
![]() ,
∆ℓ2
= 2,5 ∆ℓ1.
,
∆ℓ2
= 2,5 ∆ℓ1.
∑MA = 0; RC 4а - G 5a - F 7a + RB·10a = 0,
4 RC + 10 RB = 5 G + 7 F
![]() /
/
![]() ;
;
2,5
=
![]() ;
;
RB = 5 RC;
54 RC = 340;
RC = 6,3 кН
RB = 31,5 кН
σ1
=
![]() = 21 МПа.
= 21 МПа.
σ2
=
![]() = 52 МПа.
= 52 МПа.
Пример 10.
Ступенчатый брус
а = 0,2 м; в = 0,4 м; с = 0,8 м;
Fa = 15 см2; Fв = 10 см2; FC = 5 см2
нагружен силами Pa = - 120 кН; Pв = 60 кН; PС = - 20 кН
E = 2×105 МПа

Построить эпюры N, σ, ε, ω сечений.
Решение:
Продольные силы строим от свободного конца; на участках алгебраически суммируем силы по одну сторону сечения. Перемещение определяют от защемленного.
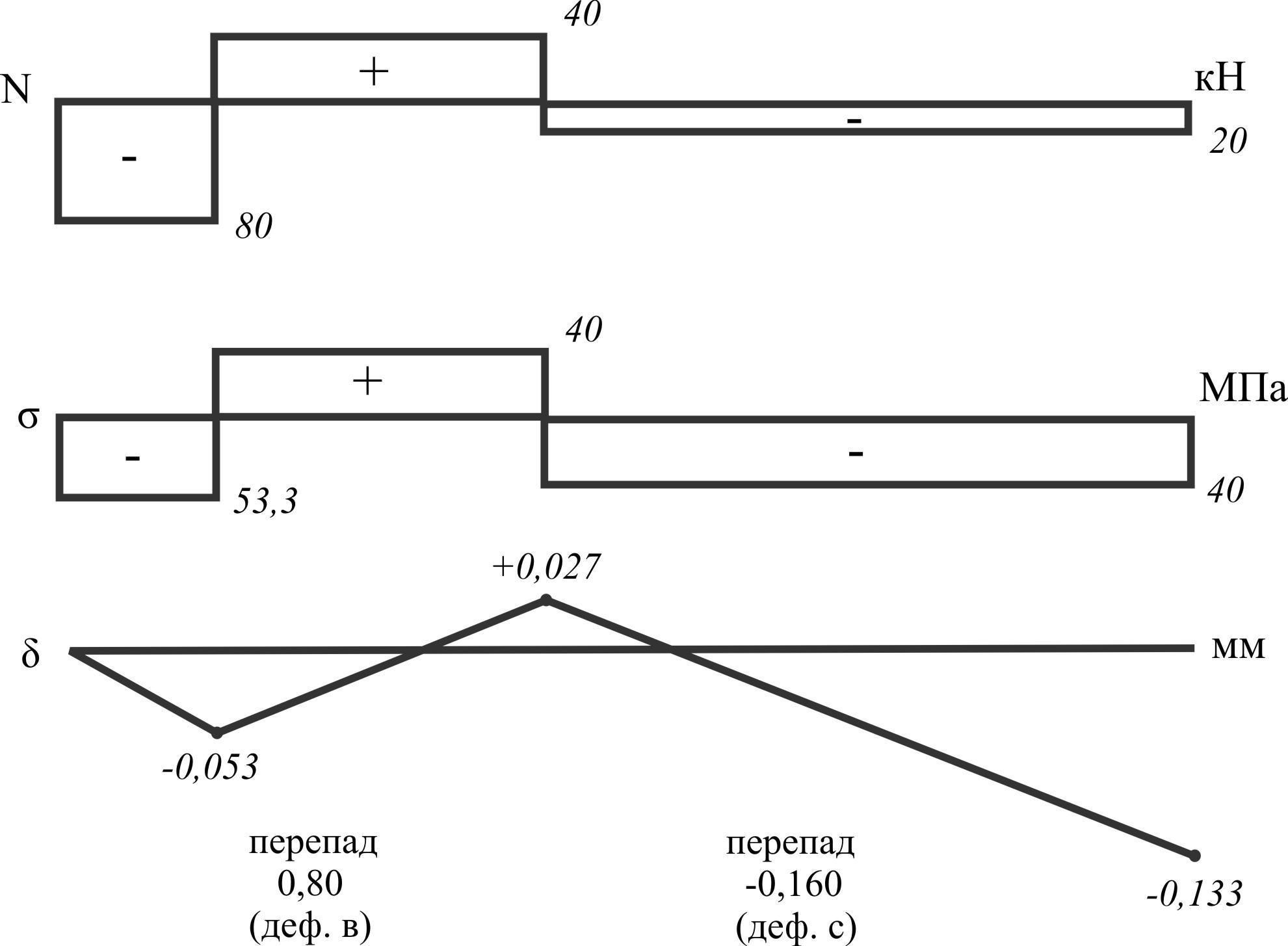
Перемещение сечений = алгебраической сумме деформации участков.
σ
=
![]() ,
,
ε
=
![]() ,
,
ω = εℓ = ∑ εiℓi.
δ1 = ε1ℓ1 = ∆ℓ1.
δ2 = δ1 + ∆ℓ2 = ε1ℓ1 + ε2ℓ2 = 0,080 - 0,053 = 0,027.
δ3 = δ2 + ε3ℓ3 = 0,027 - 160×10-3 = -0,133.
Пример 11.
Дан брус (размеры и приложенные силы) - см. рис. ниже.
Построить эпюры N, σ, ω.
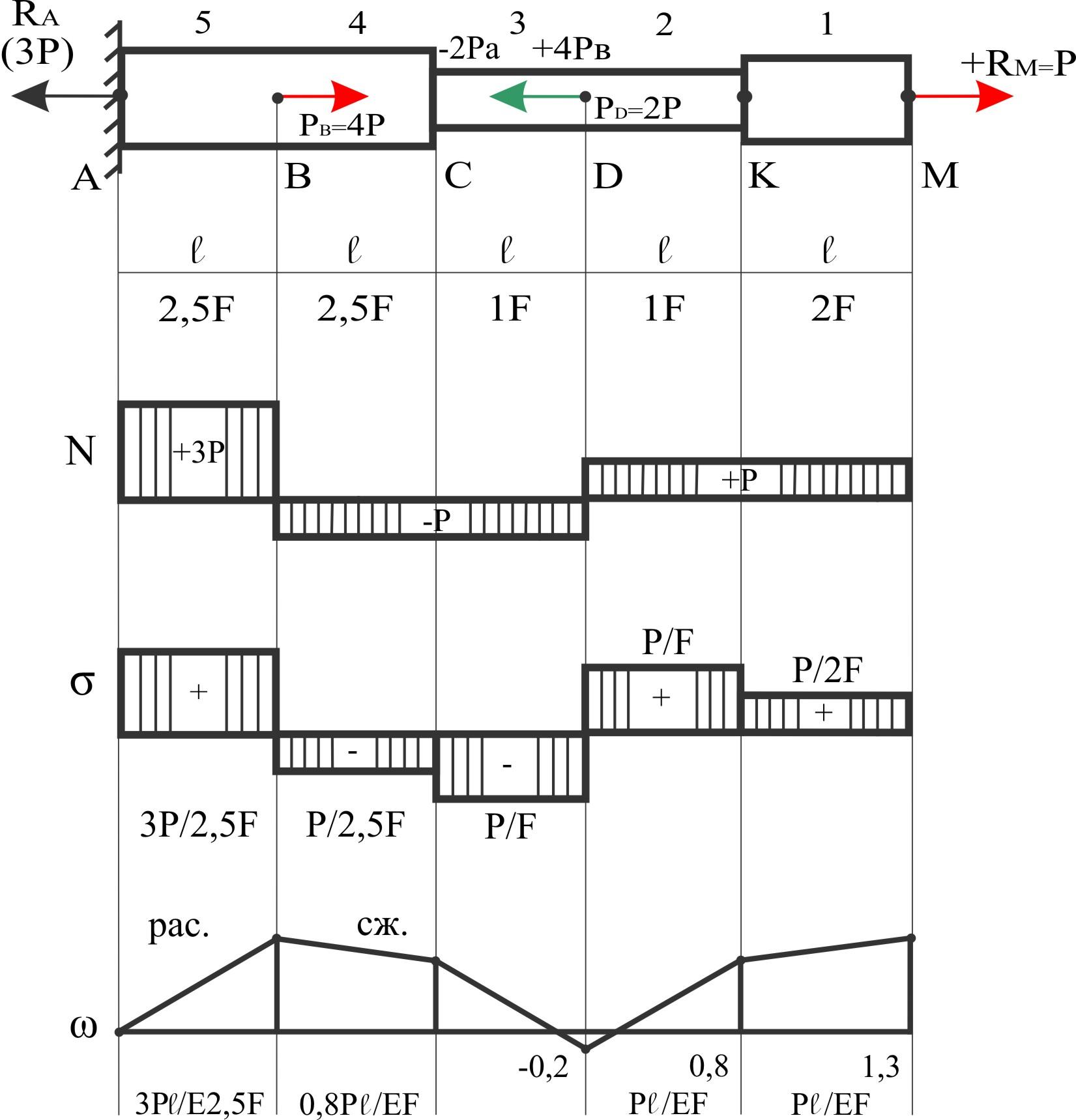
Решение:
Построение N и σ от свободного конца, перемещений ω от заделки
σ
=
![]() .
.
Скачки в сечениях, где приложены силы (+ при совпадении направления сил и оси Z).
(5)
ωB
= ∆ℓ1
=
![]() =
=
![]() .
.
(4)
ωC
= ωB
+ ∆ℓ2
= 1,2
![]() +
+
![]() = (1,2 - 0,4)
= (1,2 - 0,4)![]() = 0,8
= 0,8
![]() .
.
(3)
ωD
= ωC
+ ∆ℓ3
= 0,8![]() +
+
![]() = (0,8 - c)
= (0,8 - c)![]() = -0,2
= -0,2
![]() .
.
(2)
ωK
= ωD
+ ∆ℓ2
= -0,2![]() +
+
![]() = 0,8
= 0,8![]() .
.
(1)
ωM
= ωK
+ ∆ℓ1
= 0,8![]() +
+
![]() = 1,3
= 1,3![]() .
.
П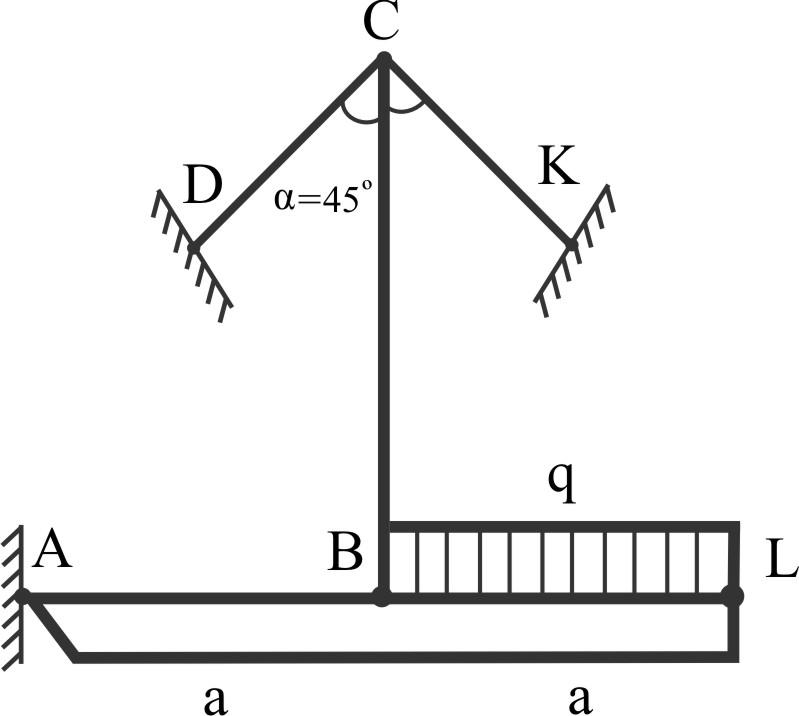 ример
12.
ример
12.
a = 1,2 м
q = 50 кН/м
α = 45º
[σ] = 150 МПа
Определить диаметры BC, CD и CK, обеспечивающие прочность конструкции.
Решение:
Изобразим силы в стержнях. Применим метод сечений.

I Уравнение равновесия AL: ∑MA = 0
R1a - qa·1,5a = 0; R1 = N1 = 1,5 qa;
→ →
R1 = - N1.
II Уравнение равновесия узла C:
∑X = 0; N2 sin 45 - N3 sin 45 = 0; N2 = N3.
∑Y
= 0; 2 N2
cos
45 - N1
= 0; N2
= N3
=
![]() .
.
На основании требований прочности:
A1
= F1
=
![]() =
=
![]() =
=
![]() =
=
![]() = 0,6·10-3
м2,
= 0,6·10-3
м2,
d1
=
![]() = 27,5 мм
≈ 28.
= 27,5 мм
≈ 28.
A2
= F2
= A3
= F3
=
![]() =
=
![]() = 0,424·10-3
м2,
= 0,424·10-3
м2,
d2
= d3
=
![]() = 23,2 мм ≈ 23.
= 23,2 мм ≈ 23.
При d2 = d3 = 23, σ2 = σ3 = 157 МПа > σ на 4,66%,
d2 = d3 = 24, σ2 = σ3 = 141 МПа < σ на 6%.
Окончательно
берем d2
= d3
= 24, т.к. по ГОСТ
![]() ≤ 3% (превышение расчета над допустимыми
≤ 3%).
≤ 3% (превышение расчета над допустимыми
≤ 3%).
Пример 13.
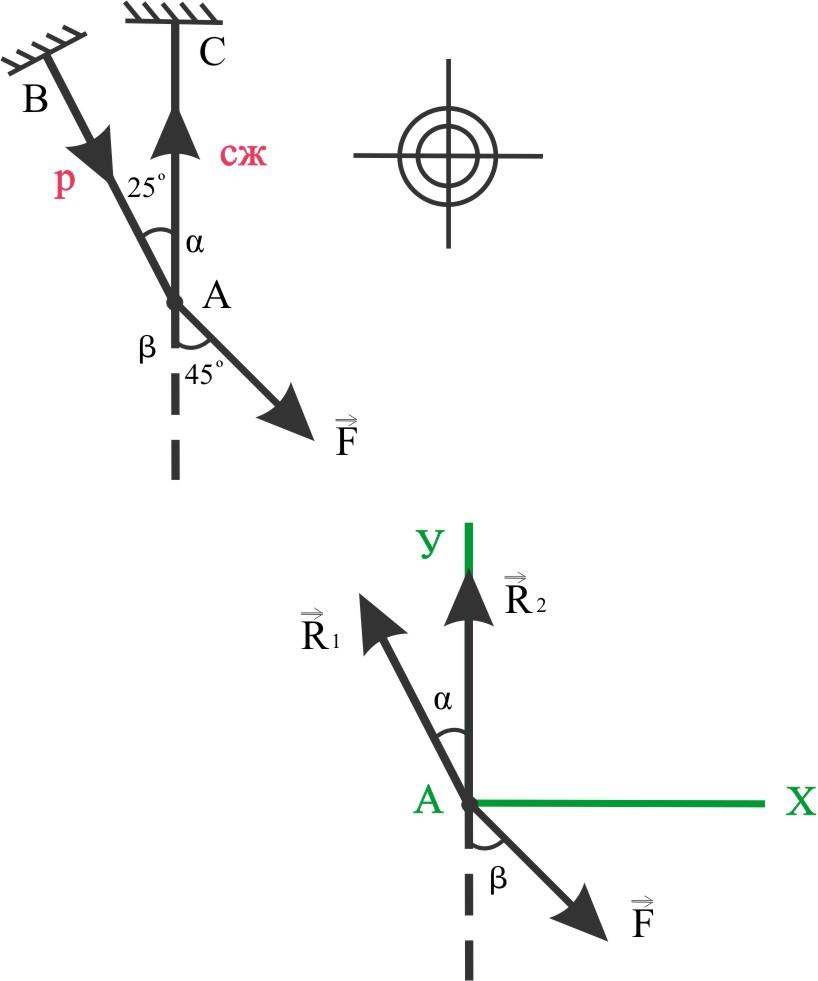
Труба дюралюминий 30×24
[σ] = 75 МПа
→
Определить допускаемую F - силу в точке A.
Решение:
Изобразим силы, после чего:
I Вырежем А.
II Составим уравнение равновесия
∑X = F sin β - R1 sin α = 0,
R1 = 1,67 F; R1 = N1.
∑Y = R1 cos α + R2 - F cos β = 0,
R2 = F cos β - R1 cos α = -0,806 F.
N1 > N2, N1 = 1,67 F = A [σ],
F
=
![]() = 11,4 кН.
= 11,4 кН.
|σAC
| =
![]() =
=
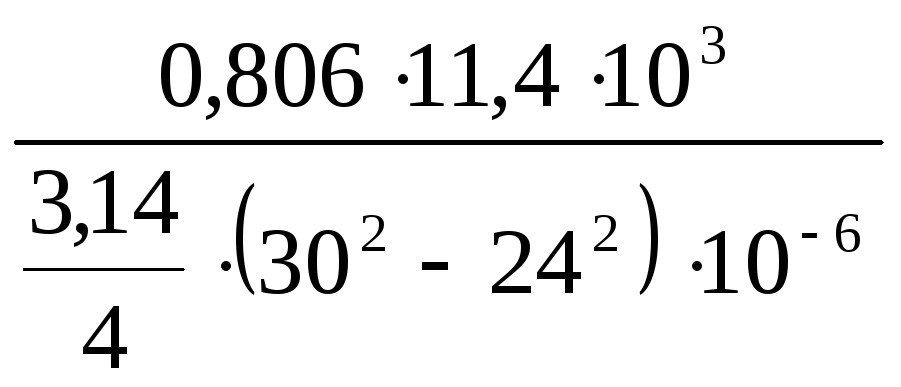 = 36,1 МПа
< [σ].
= 36,1 МПа
< [σ].
Нерациональность конструкции σAC < σAB на 53%. AC желательно меньшего сечения.
Пример 14.
Стержни из одинакового материала
Балка жесткая и невесомая
Сечения одинаковые у стержней.
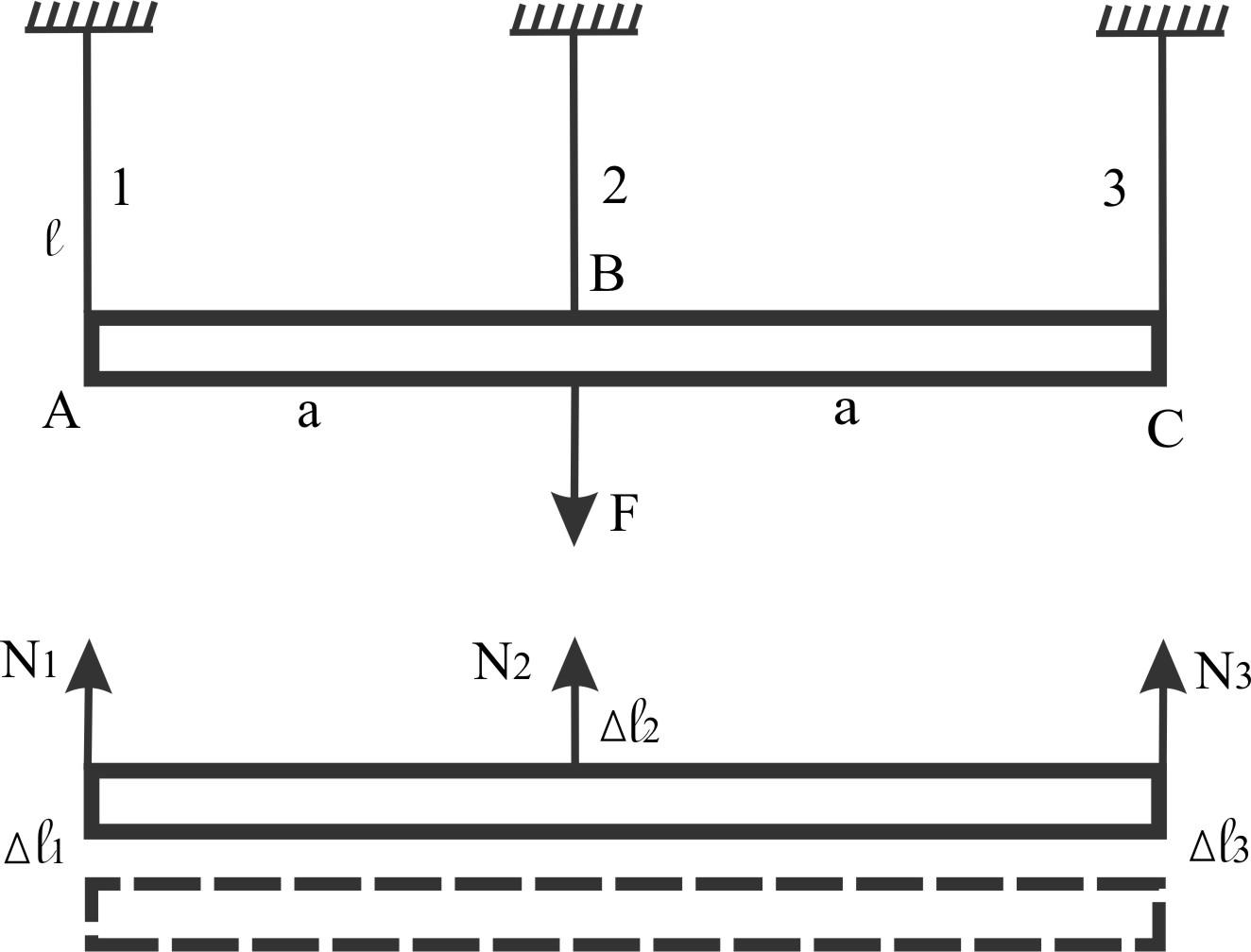
Определить силы в стержнях, на которых подвешена балка.
Решение:
Неизвестных сил 3: N1, N2, N3.
Уравнений равновесия 2: ∑Y = 0; ∑МВ = 0.
Система статически неопределима
1 раз "3 - 2" .
Симметрия системы ∆ℓ1 = ∆ℓ2 = ∆ℓ3
N1a - N3a = 0; N1 = N3.
Требуется учесть геометрическую сторону
![]() =
=
![]() =
=
![]() ;
;
N1
= N2
= N3
=
![]() - полученный результат
- полученный результат
симметрия + одинаковость жесткостей EA = const.
Может оказаться:
-
Неодинаковость сечений.
-
Неодинаковость длин.
-
Неодинаковость материала.
-
Комбинации различий.
(достигается разное распределение нагрузок).
Пример. A1 = A3 = 2А; A2 = А; ∆ℓ1 = ∆ℓ2 = ∆ℓ3,
![]() =
N2
=
=
N2
=
![]() подставим в уравнение равновесия
подставим в уравнение равновесия
N1 = N3 = 0,4 F; N2 = 0,2 F.
В более жестких системах большие силы.
Пример 15.
Дана конструкция: защемлен с 2 концов
А = 3 см2
F = 60 кН
Cm 4 (σТ = 260 МПа)
[пТ] = 1,6

Построить эпюры: N, σ, перемещение α поперечных сечений.
Решение:
В заделках A и B возникают реакции.
Уравнение равновесия ∑ Z = 0; - RA + F1 + F2 - RB = 0.
Неизвестных 2, а уравнение 1, следовательно система 1 раз статически неопределенная.
II геометрическое уравнение - уравнение перемещений, но для его составления заменим одну заделку ее реакцией RB = Х (B - свободно), следовательно статически определенный брус с 1 неизвестным RA, у которого λВ = 0 = λВF1 + λВF2 + λВX.
По закону Гука перемещение сечений определяется суммой деформаций участков между приложенными силами:
λВF1
= ∆AC
=
![]() - удлинение.
- удлинение.
λВF2
= ∆AD
+ ∆ED
=
![]() +
+
![]() - удлинение.
- удлинение.
λВX
= -![]() - укорочение.
- укорочение.
Из
λВ
следует
![]() ,
,
X
=
![]() - теперь задача статически определимая,
брус нагружен силами
- теперь задача статически определимая,
брус нагружен силами
![]() .
.
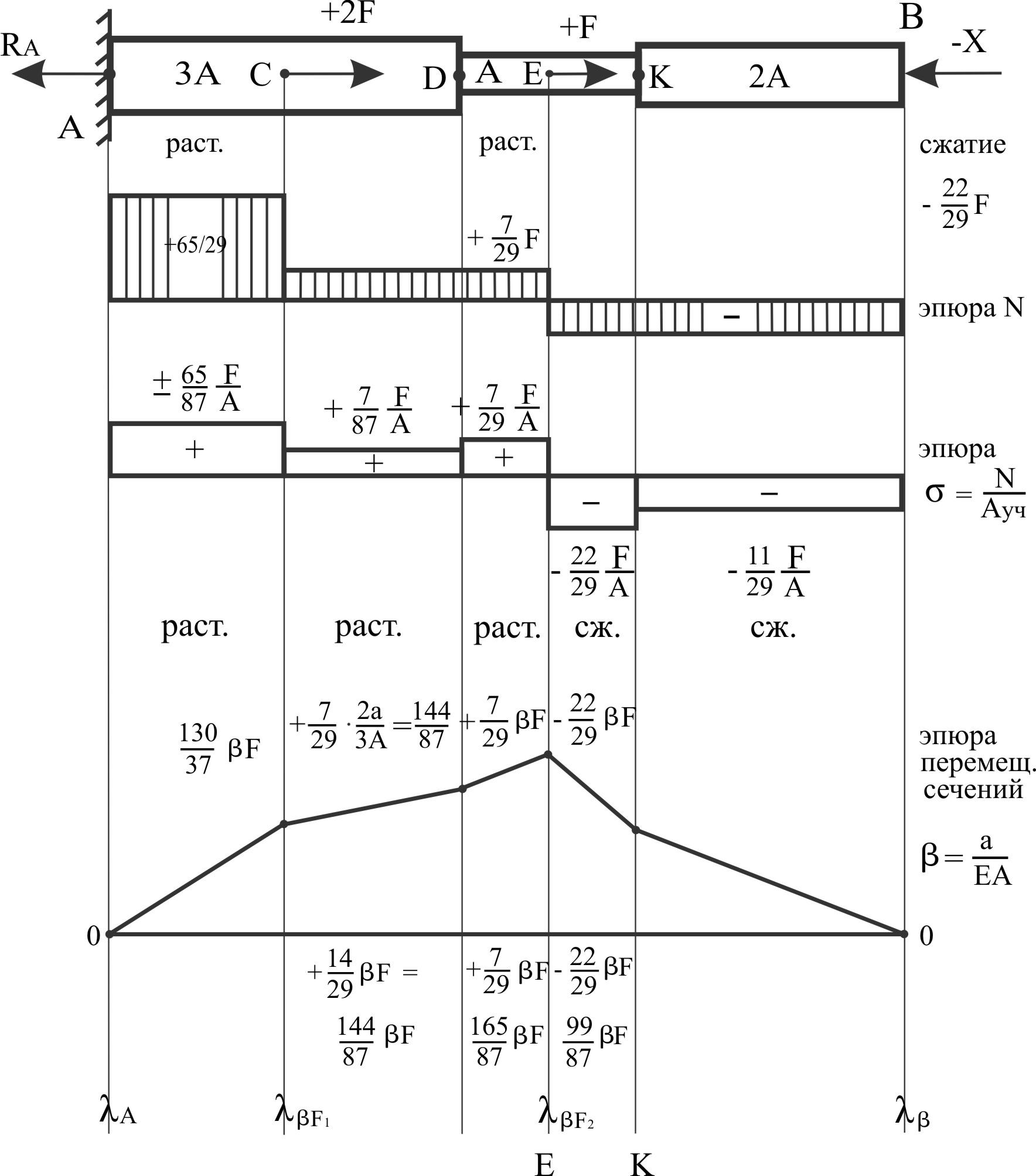
σ наибольшая в E · K - опасная зона EK
проверка прочности
пт
=
![]() =
=
![]() =
=
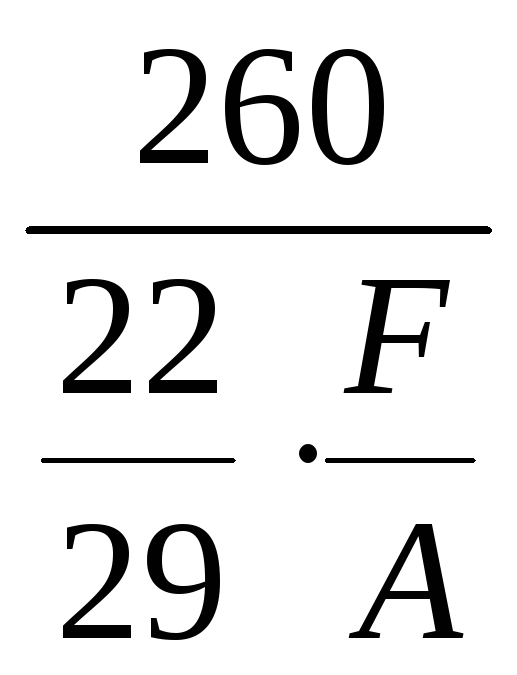 =
=
![]() = 1,72.
= 1,72.
пт > [п] обеспечена.
Пример 16.
Дана балка переменного сечения, защемленная в точке А, второй конец В свободен. Имеется зазор δ на свободном конце.
Из примера № 15 создадим справа зазор.
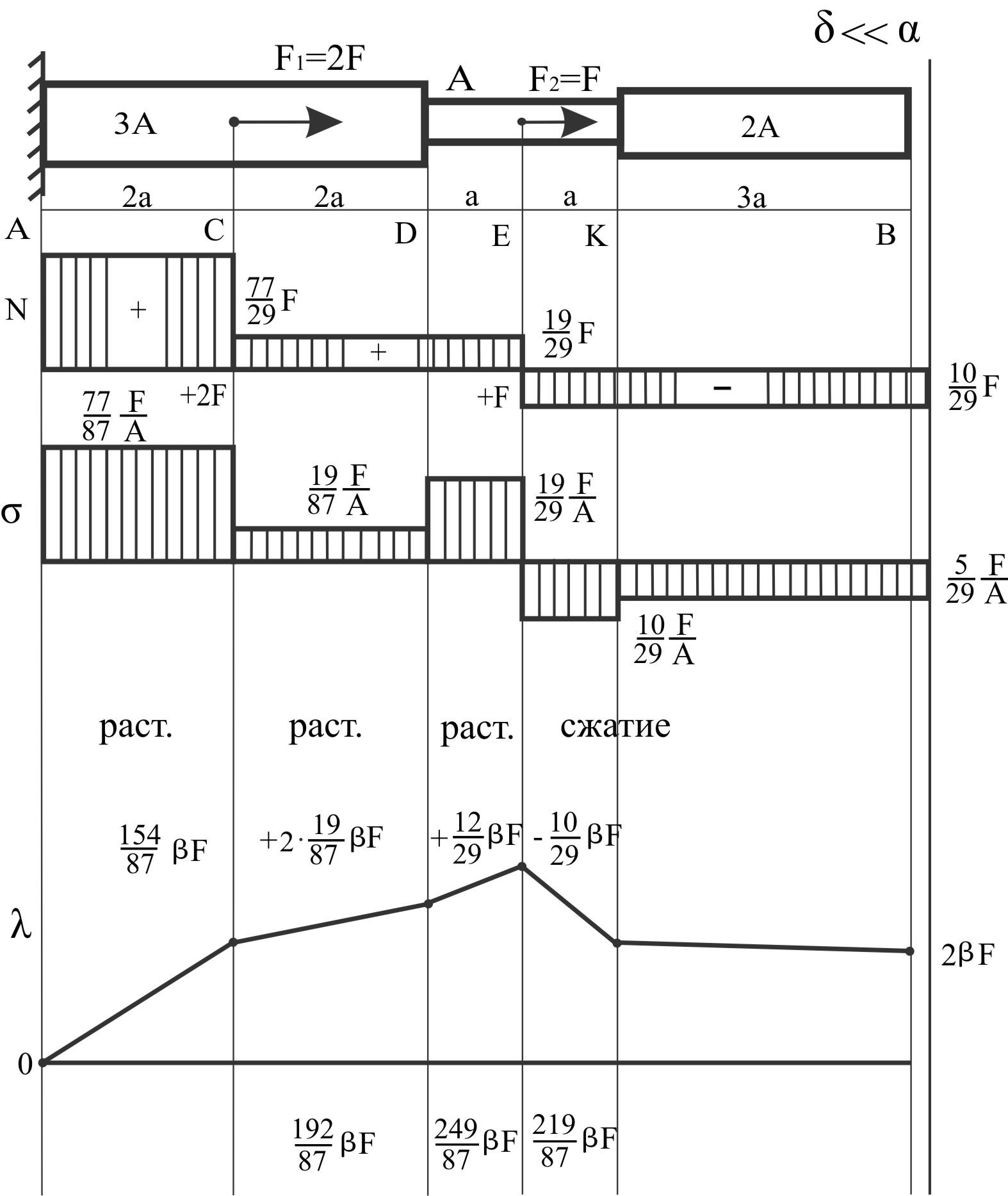
А = 3 см2
F = 60 кН
β
=
![]()
σ
=
![]()
соответствует
начальному
зазору
Суммарное перемещение правого торца λВ = δ.
Для
определенности предположим δ =
![]() = 2 βF.
= 2 βF.
При
свободном B
(без защемления): λВ
= λВF1
+ λВF2
=![]() +
+![]() +
+![]() =
=![]() βF
> δ, т.е. возникает в B
реакциях и задача статически неопределима,
следовательно кроме уравнения равновесия
нужно уравнение перемещений.
βF
> δ, т.е. возникает в B
реакциях и задача статически неопределима,
следовательно кроме уравнения равновесия
нужно уравнение перемещений.
Для
случая X
=
![]() F
F
λВ = λВF1 + λВF2 + λВX = δ,
λВF1
+ λВF2
=
![]() βF
+
βF
+
![]() =
=
![]() βF
-
βF
-
![]() βX.
βX.
Эпюры
сил N
строим от "свободного" конца B,
эпюры напряжений по эпюрам N,
следовательно σ =
![]() .
.
Эпюру λ, используя закон Гука, для деформаций участков.
Пример 17.
Определить диаметр поперечного сечения стержня, в котором τmax ≤ 80 МПа. Продольная сила N = F = 90 кН.
Решение:
τ α
max
=
α
max
=
![]() при α = 45°, откуда σz
= 2 τα
max
= 2·80 МПа.
при α = 45°, откуда σz
= 2 τα
max
= 2·80 МПа.
Но
σz
=
![]() ,
т.е. А ≥
,
т.е. А ≥
![]() .
.
Для
круга А =
![]() ≥
≥
![]() .
.
Что
позволяет найти d≥![]() =
=![]() =26,8·10-3м=
26,8мм.
=26,8·10-3м=
26,8мм.
Пример 18.
В наклонном сечении сжатого стержня σα = -60 МПа, τα = 24 МПа.
Определить σmax и τmax.
Решение.
Д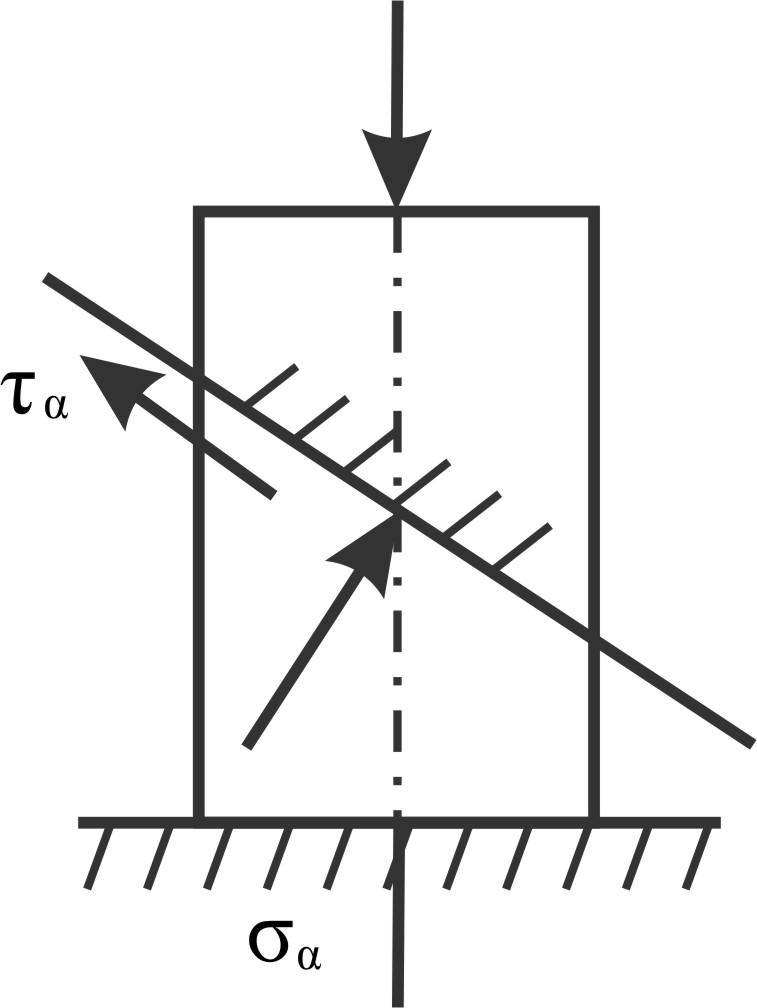 ля
наклонного сечения σα
= σz
cos2α
и τα
=
ля
наклонного сечения σα
= σz
cos2α
и τα
=![]() sin
2 α.
sin
2 α.
Из этих формул определим положение сечения
![]() =
=
![]() = tg
α,
т.е. tg
α
=
= tg
α,
т.е. tg
α
=
![]() = -0,4.
= -0,4.
Но
cos2α
=
![]() =
=
![]() = 0,862,
= 0,862,
после
чего σz
=
![]() = -
= -
![]() = - 69,6 МПа.
= - 69,6 МПа.
|
τmax
| =
![]() =
=
![]() МПа = 34,8 МПа.
МПа = 34,8 МПа.
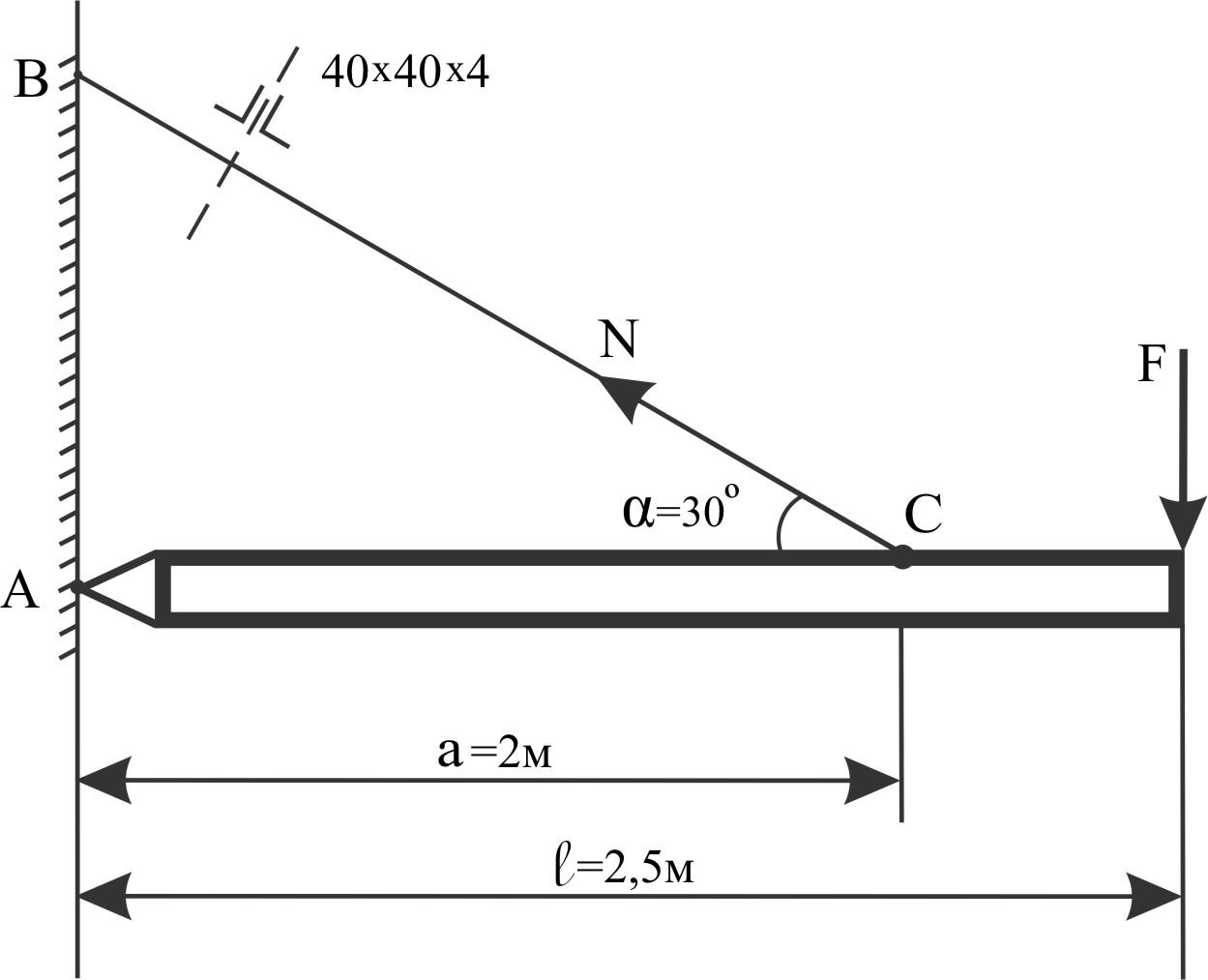
Пример 19.
Конструкция изображена на рисунке:
тяга BC сварена из 2 уголков из ст 3, для которой [σ] = 160 МПа, F = 40 кН.
Проверить расчетом прочность тяги.
 Решение:
Решение:
Продольную силу N определим из условия равновесия:
∑M = 0; Fℓ - N sin α = 0, откуда
N
=
![]() =
=
![]() = 100 кН.
= 100 кН.
После
чего σ =
![]() ,
A
= 2A1
(сварено 2).
,
A
= 2A1
(сварено 2).
A1 берем из справочника (для уголка 40×40×4 по ГОСТ 8509-86 A1 = 3,08 см2).
Считаем
σ =
![]() Па = 162·106
Па.
Па = 162·106
Па.
Допускается кратковременная перегрузка до 5%.
У
нас
![]() = 1,25%, т.е. прочность удовлетворительна.
= 1,25%, т.е. прочность удовлетворительна.
Пример 20.
Ступенчатый чугунный брус d1 = 20 мм; d2 = 30 мм должен иметь коэффициент запаса прочности [п] = 4. Материал имеет σпч.раст. = 150 МПа, σпч.сжат. = 580 МПа. Приложенные нагрузки F1 = 40 кН, F2 = 65 кН.
Проверить на прочность.
Решение:
Строим
эпюры N
и σ =
![]() .
.
Наибольшее
напряжение на I
(сжатие). Для него п =
![]() =
=![]() =4,57.
=4,57.
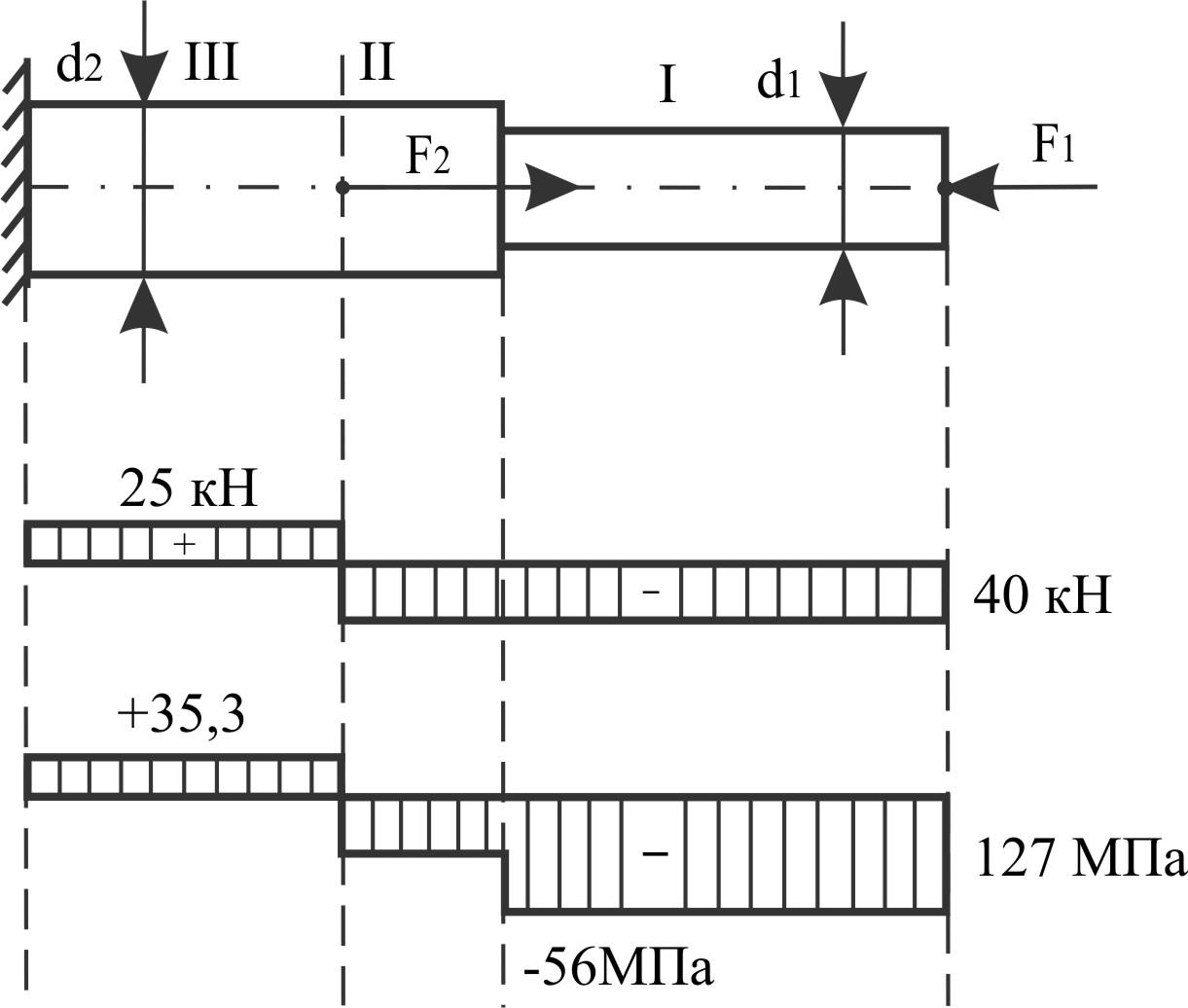
Участок
III
- растяжение п =
![]() =
=
![]() = 4,25.
= 4,25.
Оба пI и пIII больше требуемого, т.е. прочность обеспечена.
