Напряжения

Силы распределены по сечению тела, в отдельных точках сечения они различаются; поэтому введено понятие напряжения.

Беря малую площадку площадью А в зоне нашей точки и возникающую в ней внутреннюю силу R определяют среднее напряжение на площадке

P_cp=R/A.

Для более точной характеристики интенсивности внутренних сил необходимо уменьшать площадку и можно определить истинное напряжение в точке р = lim R/A

а  О

Единицей напряжения является Па (на площадке 1м² действует внутренняя сила 1Н), используются и более крупные единицы - кПа и мПа.

Следует отметить, что в исследуемой точке можно провести множество сечений по разному ориентированных в пространстве, напряжения в них будут разными в самом общем случае. Поэтому говорить о напряжении можно лишь указывая площадку, о которой идёт речь.

Принято вектор напряжения «р» раскладывать на две составляющие - нормальную к площадке  (сигма) и, лежащую в площадке - касательную  (тау).

При этом эти три напряжения связаны соотношением р = (² + ²)^1/2.

При решении некоторых задач приходится раскладывать вектор «р» на 3 составляющие; тогда р = (²_zу + ²_zy + ²_zх)^1/2.

Усилия на площадке определятся: dN_z = _zA, dQ_x = _zx dA и dQ_y = _zy dA.

Элементарные моменты получим умножая элементарные силы на расстояние до соответствующей оси:

dM_z = (_zx dA)y - (_zy dA)x, dM_x = (_z dA)y, dM_y = (_z dA)x.

Растяжение и сжатие

При деформации растяжения (сжатия) в поперечных сечениях возникает только продольная сила (один силовой фактор) N (прямые брусья, подвергаемые растяжению или сжатию, часто называют стержнями).

Силы, вызывающие растяжение, считают положительными, а вызывающие сжатие - отрицательными. Продольная сила при растяжении направлена от торцового сечения, а при сжатии - к сечению.

Чтобы брус работал на растяжение, равнодействующая всех внешних сил, приложенных по одну сторону по отношению к любому сечению, должна быть направлена вдоль оси бруса от сечения (внутренние силы противоположны равнодействующей внешних сил).

Когда продольные силы в разных поперечных сечениях неодинаковы удобно закон их изменения по длине бруса представлять в виде графика (так называемой эпюры продольных сил). В плоской декартовой системе координат абсцисса - координата поперечного сечения, а ордината(функция) - продольная сила N, N = f(z). При построении эпюры брус разбивают на участки, для каждого из которых будет своё выражение функции, границы таких участков соответствуют сечениям, в которых приложены внешние силы. В местах приложения сосредоточенных сил на эпюре получаются скачкообразные изменения ординат, размер такого скачка соответствует приложенной в соответствующем месте сосредоточенной силе. Эпюру принято штриховать в направлении перпендикулярном оси эпюры, длина штрихов в масштабе определяет значение продольной силы на соответствующем участке бруса.

П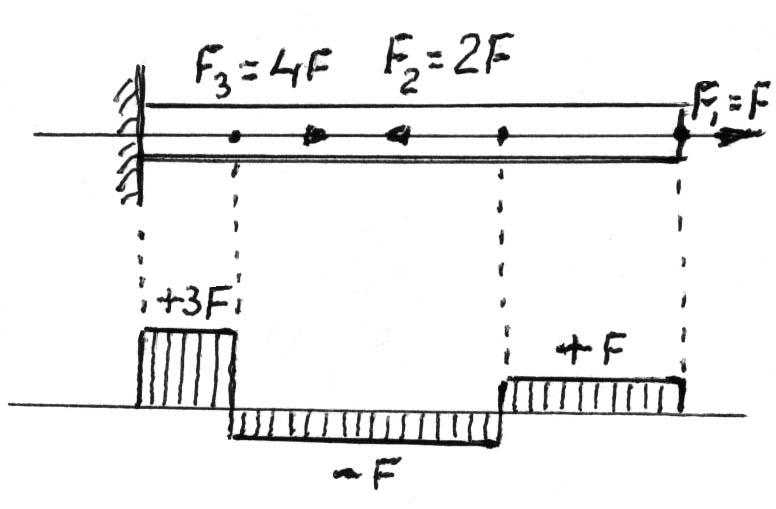ри растяжении (сжатии) бруса в его поперечных сечениях возникают только нормальные  = N/A напряжения. Этим соотношением мы пользуемся на основе гипотезы Я.Бернулли: сечение бруса, плоские и нормальные к его оси до деформации, останутся такими и при деформации; кроме того, внутри бруса деформация имеет тот же характер, что и на поверхности и нормальные напряжения по поперечному сечению распределены равномерно. При растяжении нормальные напряжения считают положительными (в зоне приложения внешних сил неравномерность распределения напряжений носит местный характер и ею можно пренебречь). Только в местах резкого изменения формы и размеров поперечного сечения возникают местные напряжения (концентрация напряжений). При неодинаковости нормальных напряжений в разных по величине поперечных сечениях целесообразно построить эпюры нормальных напряжений.