Задачи на изгиб

Пример 1.

Построить эпюры Q_y и M_x для защемленной одним концом балки и нагруженной на свободном конце парой сил с моментом М.

Решение:

Проводим произвольное поперечное сечение на расстоянии Z от свободного конца и рассмотрим условие равновесия левой отсеченной части: поперечная сила Q_y = 0, т.к. нагрузка - пара сил, она не дает проекций ни на одну ось пространственной декартовой системы координат.

Таким образом, имеет место чистый изгиб.

M_x = М по модулю.

M_x от Z не зависит.

Изгиб происходит выпуклостью вниз, следовательно M_x > 0.

Эпюры:

Для балок, защемленных одним концом, целесообразно отбрасывать часть, примыкающую к заделке (тогда нет необходимости определять реакции заделки).

Пример 2.

Построить эпюры Q_y и M_x для защемленной балки, на свободном конце которой приложена сила F.

Решение:

Проводим на расстоянии Z от свободного конца сечение и рассмотрим левую отсеченную часть.

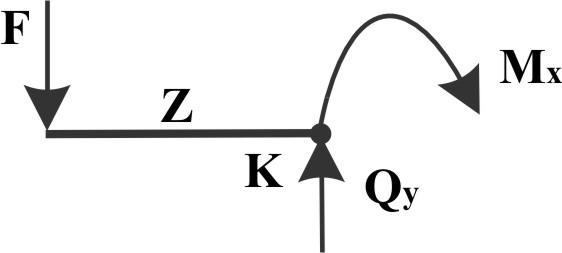Для равновесия Q_y = - F, т.е. поперечная сила во всех сечениях одинакова. Защемляем в "К", оставленную часть F изогнет ее выпуклостью вверх, т.е. M_x < 0 и M_x = - Fz (переменная, изменяющаяся по линейному закону).

Эпюры имеют вид:

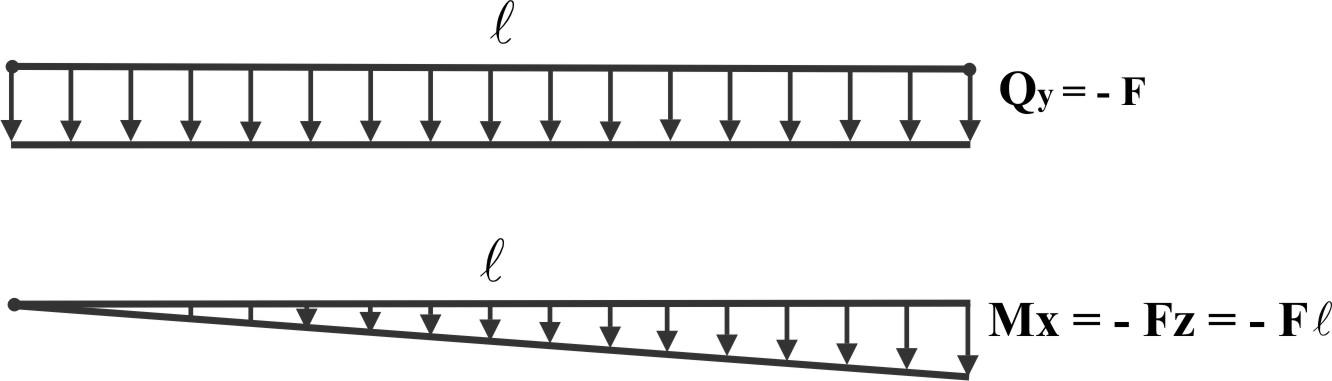
Пример 3.

Построить эпюры для изображенной балки.

Решение:

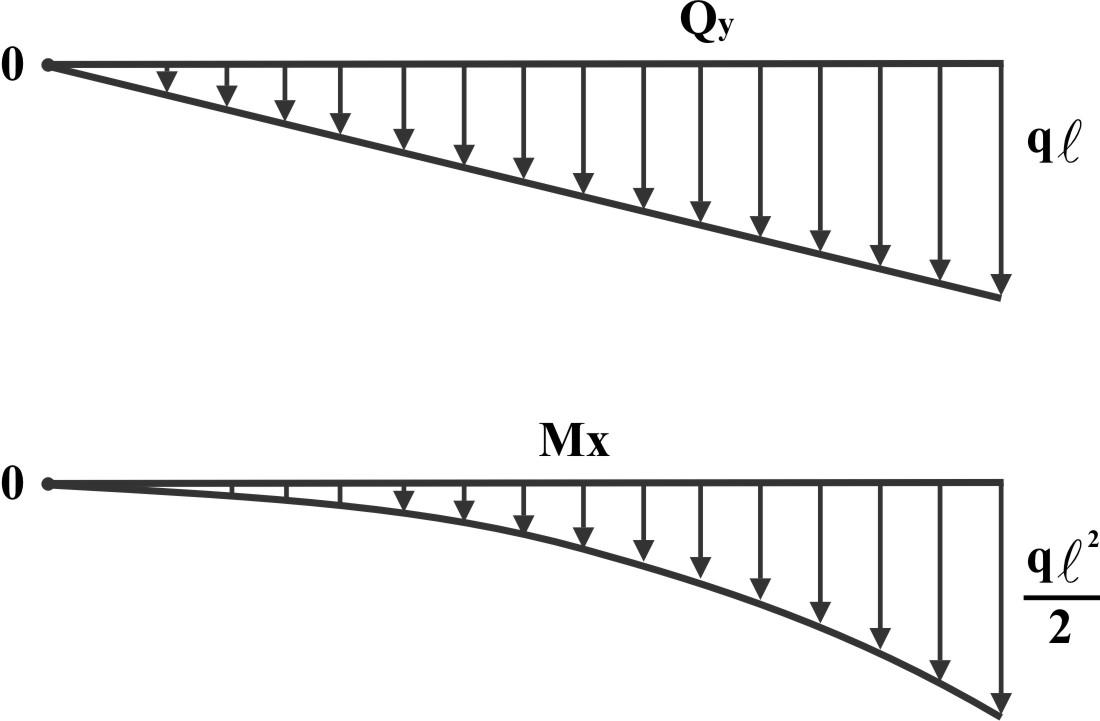
Проводя сечение в точке Z отметим Q_y = - qz (линейная зависимость).

M_x= -qz· (приложение посредине участка). Квадратичная зависимость - парабола (вершина на левом конце).

Пример 4.

Построить для изображенной балки эпюры Q_y и M_x.

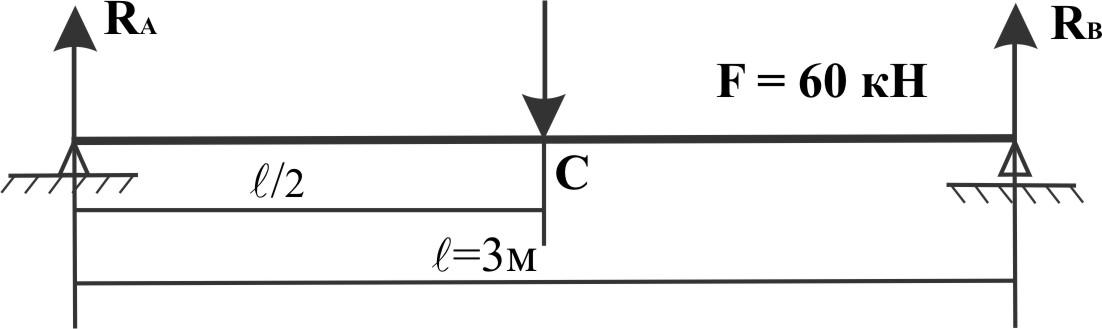
Решение:

1. Определяем реакции. В силу симметрии R_A = R_B = 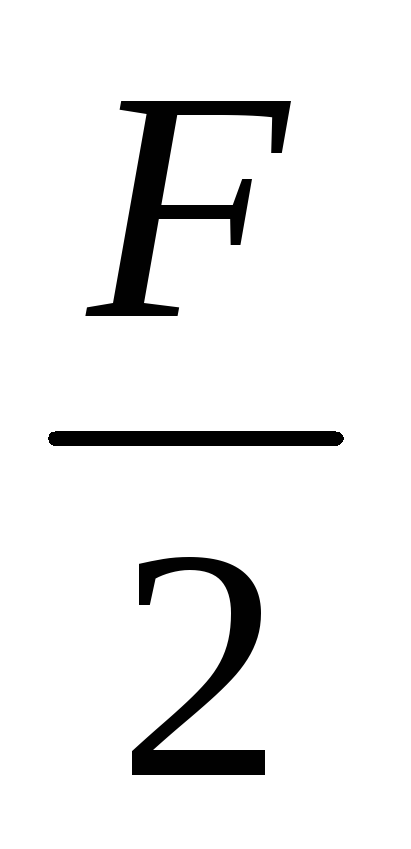= 30 кН.

У балки 2 участка: 0 ≤ Z ≤ и ≤ Z ≤ ℓ.

2. Проводя сечение в левой части Q_yI = R_A = , M_xI = R_AZ = .

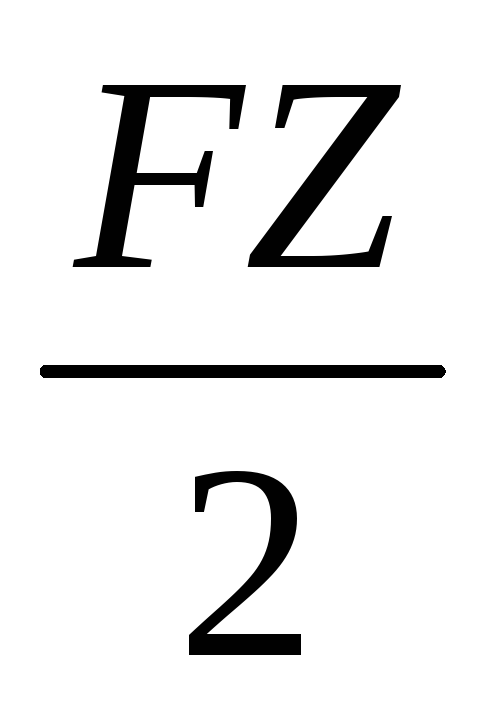3. Проводя сечение в правой части Q_yII = R_A 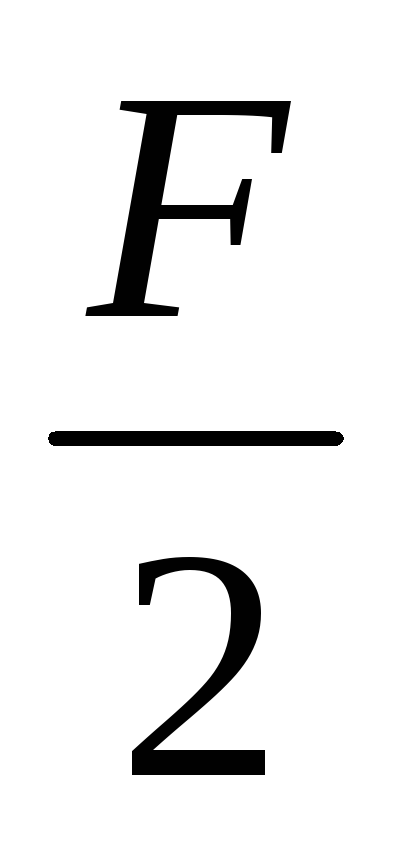- F = - F = - .

M_xII = R_AZ - F (Z - ) = - F (Z - ) = - + .

И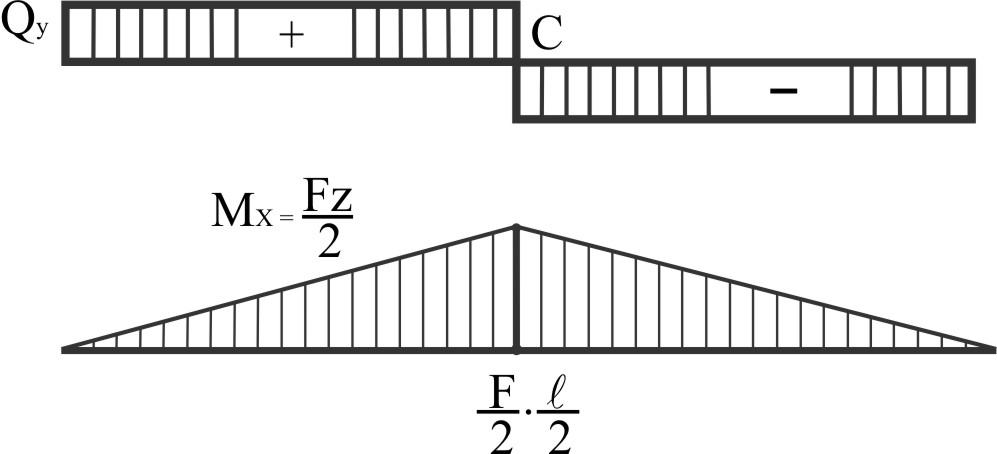згибающий момент в среднем сечении Z = 0,5ℓ.

В "С" скачок поперечной силы, равный этой силе (слева от С + , а справа - ). Скачок носит условный характер.

Пример 5.

Для изображенной двухопорной балки построить эпюры Q_y и M_x.

Р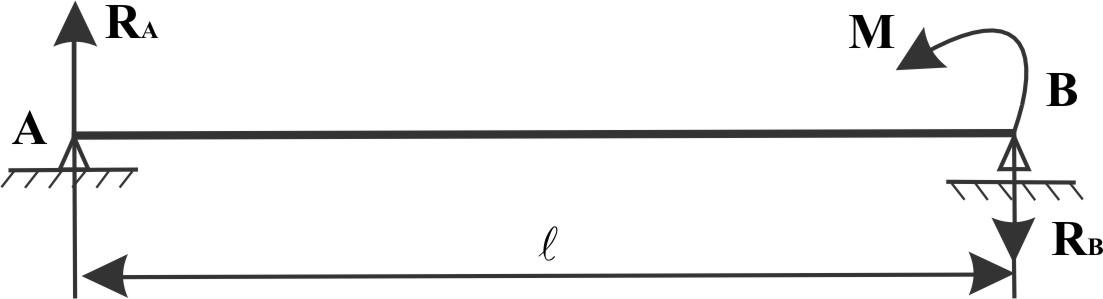ешение:

1. Определим опорные реакции R_A = - R_B = .

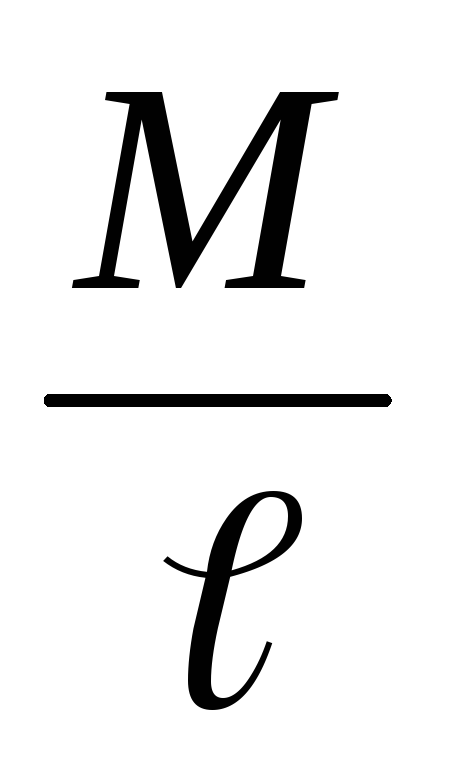2. Распределенной нагрузки нет q = 0, следовательно Q_y = 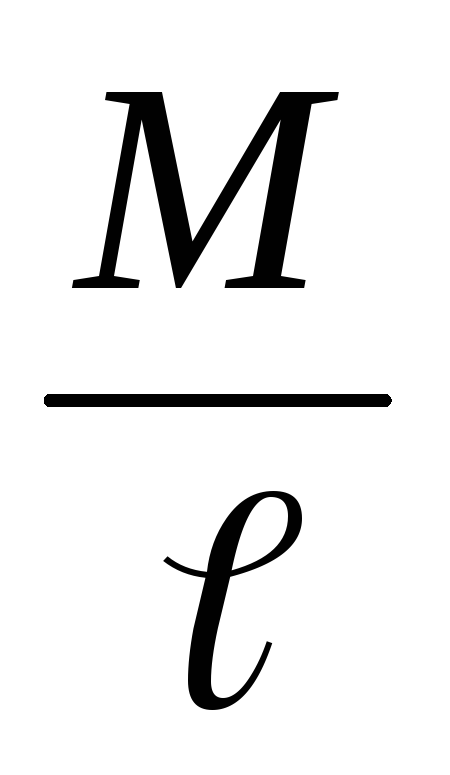= const.

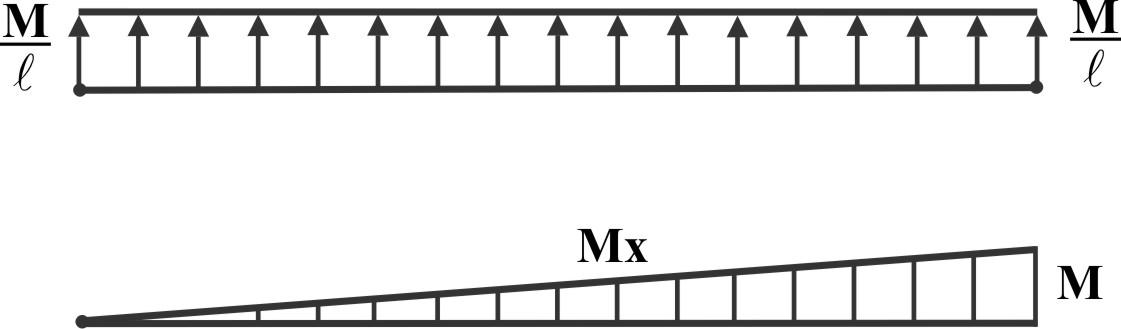
3. M_x определим, мысленно проведя сечение близко к В, чтобы не учитывать момент от R_B.

Mомент изгибает балку сжатой частью сверху, таким образом M_x > 0. M_x - линейна, т.к. Q_y = const.

Пример 6.

Построить эпюры Q_y и M_x для двухопорной балки, длиной ℓ и нагруженной посредине моментом М.

Р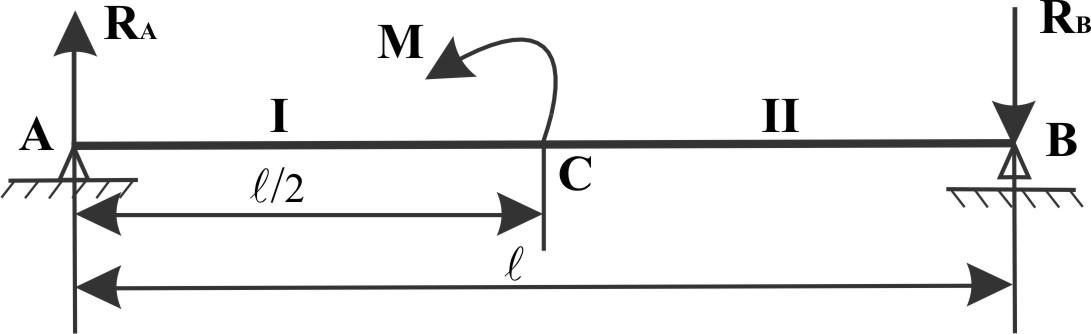ешение:

Приложена пара сил, следовательно реакции должны образовать пару той же величины, но противоположного знака R_A = R_B = .

В любом сечении I участка Q_yI = R_A = = const, M_xI = R_AZ = - линейная зависимость.

M_{xI max} = · = .

Для II участка для сил, приложенных левее сечения Q_yII = R_A = .

M_xII = R_AZ - M = · - M = - .

При Z = ℓ, M_xII = ·ℓ - M = 0.

Эпюры:

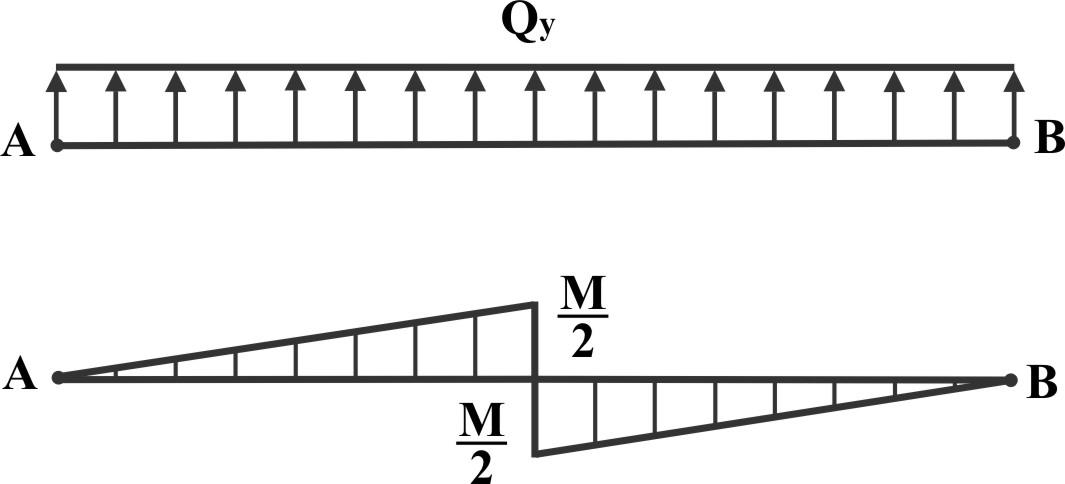
Пример 7.

Консольная балка на свободном конце "С" нагружена силой F. Построить эпюры Q_y и M_x (рис.).

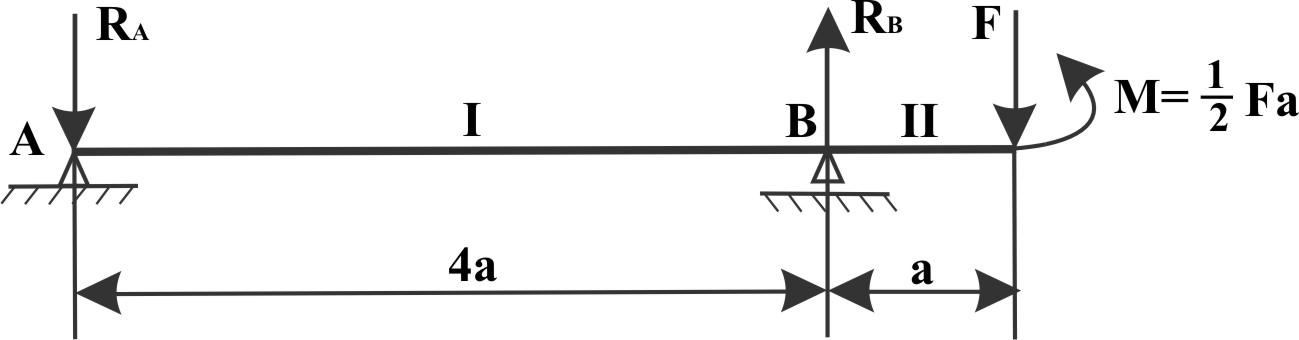
Решение:

Для определения реакций опор используем условия равновесия:

∑ М_А = 0, F·5а - М - R_B·4а = 0, откуда R_B·4а = F·5а - F·а = F·а,

R_B = F.

∑ М_В = 0, - R_A·4а + F·а - F·а = 0, т.е. R_A = F.

На левой опоре Q_yА = - R_A = - F = const на всем I участке.

В "В" Q_yВ скачок, т.к. Q_yС = F.

В задаче нет распределение нагрузки, т.е. M_x изменяется линейно и нам нужно определить M_x в точках А, В, С.

В "А" M_x = 0, т.к. нет внешней пары.

В "В" M_x < 0, т.к. R_A изгибает балку выпуклостью вверх в точке "В".

M_xB = - R_A·4а = - F·4а = - Fа.

В "С" M_xC = Fа, изгиб на II участке выпуклостью вниз.

Пример 8.

Для балки, изображенной на рисунке, построить эпюры Q_y и M_x.

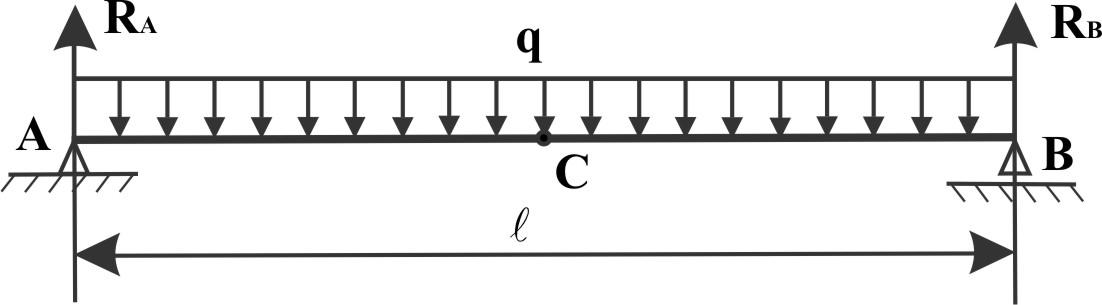
Решение:

В силу симметрии R_A=R_B=.

В "А" Q_y = .

В "В" Q_y = - .

Между ними Q изменяется по линейному закону и эпюра Q будет:

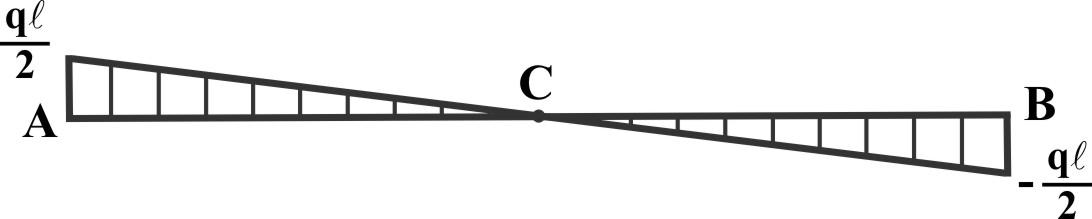
Эпюра M_x - парабола с выпуклостью вверх при M_xA = M_xB = 0.

В "С" M_{x max}. Рассчитаем это значение: берем сумму моментов всех сил, расположенных левее "С":

M_xC = M_{x max} = R_A - · = · - · = .

Эпюра M_x

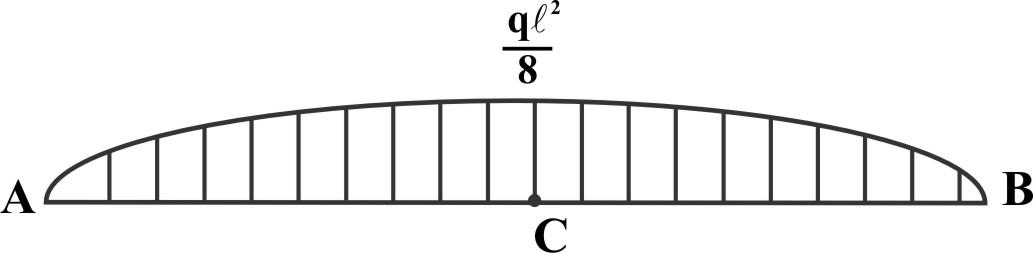
Пример 9.

Для простой консоли, нагруженной в соответствии с рисунком, построить эпюры Q_y и M_x.

Решение:

Строим эпюры, начиная от свободного конца, на котором Q_xА=0 (нет сосредоточенных сил). На АВ Q_y изменяется по линейному закону и в "В" Q_yВ=q2a (знак "-", т.к. внутренние силы противоположны внешним).

На ВС и СD нет распределенных нагрузок (таким образом на этих участках Q_{y II} = Q_{y III} = Q_yВ = - 2 qa) наличие пары с моментом М на Q_y не отражается.

В "D" скачок силы на величину F и на IV участке Q_{y IV} = - qa и опорная реакция Q_yЕ = - qa. Изобразим эпюру Q_y:

П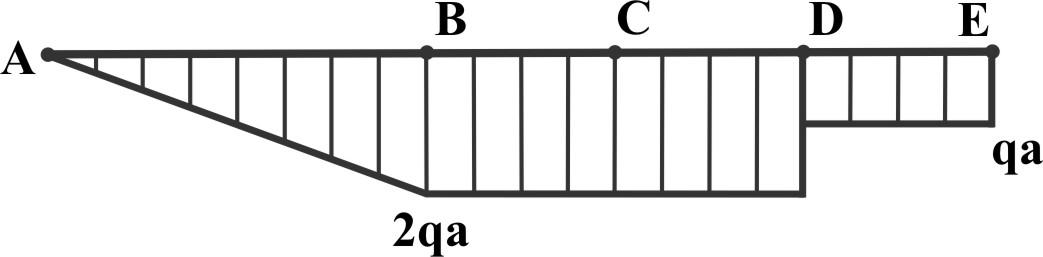ереходим к эпюре изгибающих моментов M_x: M_xA = 0 (нет сосредоточенной силы).

На АВ M_x меняется по квадратичному закону выпуклостью вверх (навстречу внешней нагрузке) и в "В" достигает значения

M_xB = - q·2a·а = - 2 qa².

На участке II, т.е. на ВС, т.к. Q_y = const M_xII изменяется по линейному закону. Почти в "С", но чуть - чуть левее M_{xC лев.} = - 2 qa·2а = - 4 qa². В "С" скачок момента на величину момента пары М (М изгибает консоль выпуклостью вниз, т.е. скачок вверх).

M_{xC прав.} = - 4 qa² + qa² = - 3 qa².

На участке CD M_x меняется по линейному закону и в "D"

M_xD = - q·2a·3а + qa² = - 5 qa².

На участке DE M_x меняется линейно и в самом конце, т.е. в "Е"

M_xE = - q·2a·4а + qa² + qa·а = - 6 qa².

При этом реактивный момент в "Е" равен M_xE, но с противоположным знаком, т.е. 6 qa².

Эпюра M_x:

Пример 10.

Для двухопорной консольной балки, изображенной на рисунке, построить эпюры Q_y и M_x.

Решение:

Начнем с определения реакций опор R_A и R_B. Применим уравнение равновесия:

∑ М_А = 0, т.е. q·4а·2a·+ 2 qa·4а + 2 qa² - R_B·5а + qa·6а = 0,

откуда R_B = 4,8 qa.

Аналогично ∑ М_В = 0, т.е. R_A·5а - q·4а·3а - 2 qa а + 2 qa² + qa·а = 0,

откуда R_A = 2,2 qa.

Теперь строим эпюру Q_y:

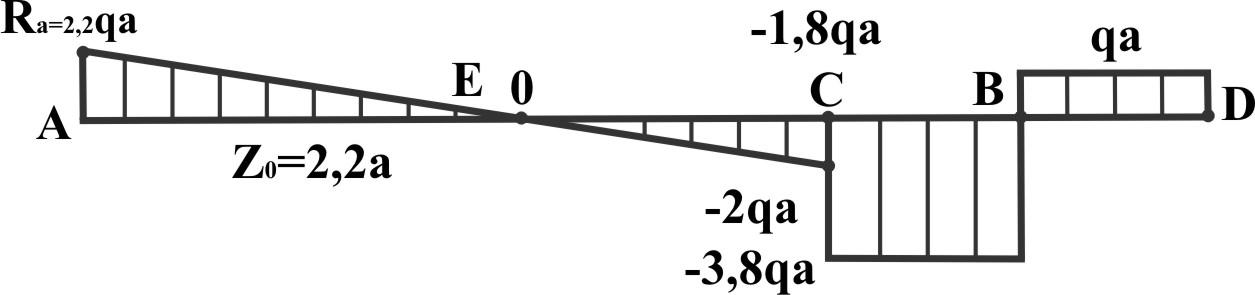
1. На участке I Q_y меняется линейно,

Q_{yС левее} = R_A - q4а = - 1,8 qa.

В "С" скачок на F₁ и Q_{yС правее} = - 1,8 qa - 2 qa = - 3,8 qa.

На СВ Q_y = const = - 3,8 qa, а в "В" скачок на R_B и на участке III

Q_yIII = const = - 3,8 qa + R_B = - 3,8 qa + 4,8 qa,

Q_yIII = qa строим эпюру M_x:

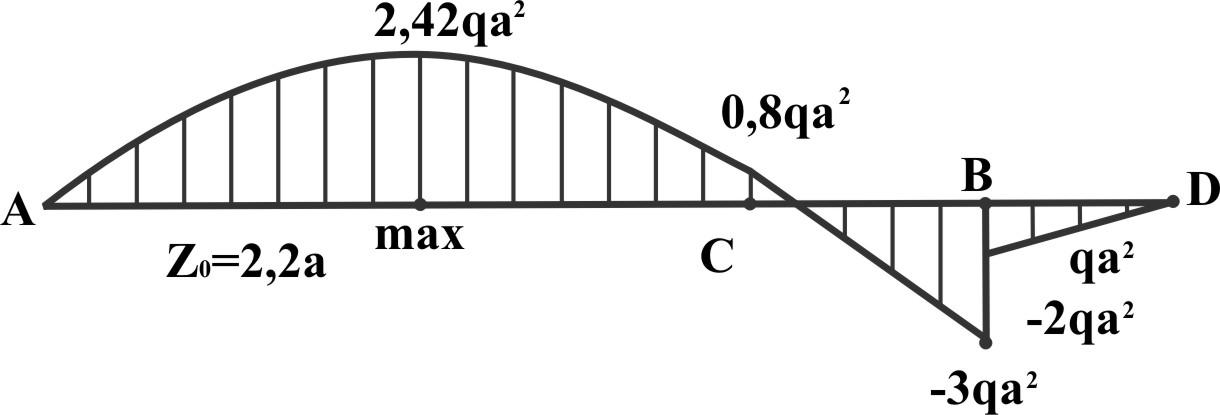
2. M_xA = 0. На участке I M_x изменяется по квадратичному закону (на нем распределена нагрузка) и там, где Q_y = 0 парабола имеет max (это в точке Z₀ = 2,2a).

M_{x max} = R_A·Z₀ - q Z₀ = 2,2 qa·2,2a - q·2,2a· = 2,42 qa².

M_xC = R_A·4а - q·4а·2а = 8,8 qa² - 8 qa² = 0,8 qa².

Остальную часть графика удобнее строить с правого конца: на участке III M_x меняется линейно, а М_{В правее} = - qa², в "В" скачок на М = 2qa² и в итоге М_хВ = 3 qa².

На участке II - линейная зависимость.

Окончательно эпюра M_x будет выглядеть:

Список литературы

Основная

1. Архитектурная физика (под редакцией акад. Н.В. Оболенского). - М.: Архитектура, 2005.

2. Ицкович Г.М. Сопротивление материалов. - М.: Высшая школа, 2001.

3. Эрдеди А.А., Эрдеди Н.А. Теоретическая механика. Сопротивление материалов. - М.: Академа, 2003.

Дополнительная

1. Мигалина И.В. Основы архитектурного цветоведения. - М.: 1998.

2. Пономарева Е.С. Цвет в интерьере. - Минск: Высшая школа, 1984.

3. СНиП 11 - 4 - 79. Естественное и искусственное освещение.

4. СНиП 2.01.01 - 82. Строительная климатология и геофизика.

5. Справочник. Защита от шума в градостроительстве. - Стройиздат, 1993.

Содержание

стр.

1. Что такое "сопротивление материалов" 3

2. Классификация внешних сил и опор 3

3. Допущения в сопромате 4

4. Метод сечений 5

5. Напряжения 7

6. Растяжение и сжатие 8

7. Деформации 9

8. Напряженное состояние 11

9. Запас прочности 12

10. Статически неопределимые системы 12

11. Задачи на растяжение (сжатие) 13 12. Чистый сдвиг 30

13. Практические расчеты на срез и смятие 32

14. Неразъемные соединения 33

15. Заклепочные соединения 34

16. Сварные соединения 34

17.Кручение 35

18. Напряжения и перемещения при кручении бруса круглого

поперечного сечения 36

19. Геометрические характеристики плоских сечений 38

20. Задачи на кручение и сдвиг (срез и смятие) 40

21. Прямой изгиб 50

22. Поперечные силы и изгибающие моменты 51

23. Дифференциальные зависимости между распределенными

нагрузками, поперечной силой и изгибающим моментом 52

24. Общие указания к построению эпюр 53

25. Нормальные напряжения при изгибе 54

26. Касательные напряжения при прямом поперечном изгибе 56

27. Перемещения при изгибе 56

28. Задачи на изгиб 59

29. Список литературы 67

70