Прямой изгиб

Изгиб - деформация, при которой в поперечном сечении бруса возникают изгибающие моменты. Если при этом поперечные силы не возникают, изгиб называется чистым; если одновременно с изгибающими моментами возникают и поперечные силы, изгиб называется поперечным.

Деформация изгиба возникает при нагружении бруса силами, действующими в плоскостях, проходящих через его продольную ось и действующих перпендикулярно оси (или парами сил, действующими в тех же плоскостях). Если все нагрузки действуют в одной плоскости, изгиб называют плоским.

Рассмотрим брусья с поперечными сечениями, имеющими хотя бы одну ось симметрии (ось симметрии и перпендикулярная ей центральная ось - главные центральные оси сечения.

Прямой изгиб- это изгиб, при котором плоскости нагрузок (силовая плоскость) совпадает с одной из главных плоскостей. Линия пересечения силовой плоскости с плоскостью поперечного сечения - силовая линия. При прямом изгибе она совпадает с одной из главных центральных осей поперечного сечения.

При прямом изгибе деформация происходит в силовой плоскости (в этой плоскости лежит ось изогнутого бруса). Если силовая плоскость не совпадает ни с одной из главных плоскостей бруса (силовая линия не совпадает ни с одной из главных центральных осей его поперечного сечения) изгиб называют косым. При этом ось изогнутого бруса не лежит в силовой плоскости и направление нагрузок и прогибов не совпадают.

Применяя метод сечений и рассматривая условия равновесия отсечённой части

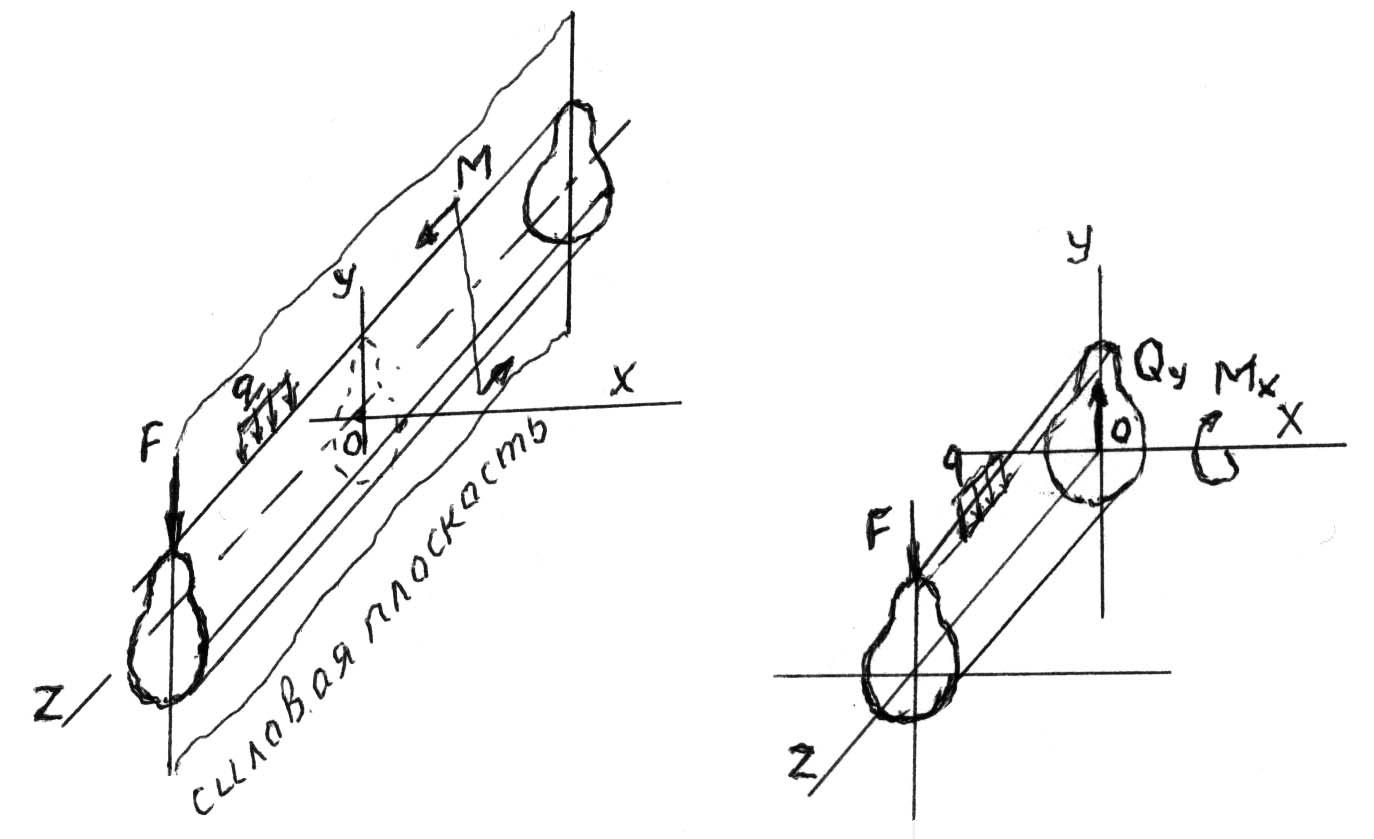
При прямом изгибе в поперечных сечениях бруса возникают 2 силовых фактора - поперечная сила Q и изгибающий момент М_х. внешние силы лежат в плоскости ZOY перпендикулярно OZ (их проекции относительно осей Х и Z равны нулю).

Прямой изгиб, при котором и изгибающий момент, и поперечная сила не равны нулю, называют поперечным прямым изгибом. При этом часть волокон испытывают растяжение (в выпуклой части), а часть - сжатие (в вогнутой). Между ними есть слой волокон, которые только искривляются (нейтральный слой). Такие брусья принято называть балками. Балки бывают нескольких типов:

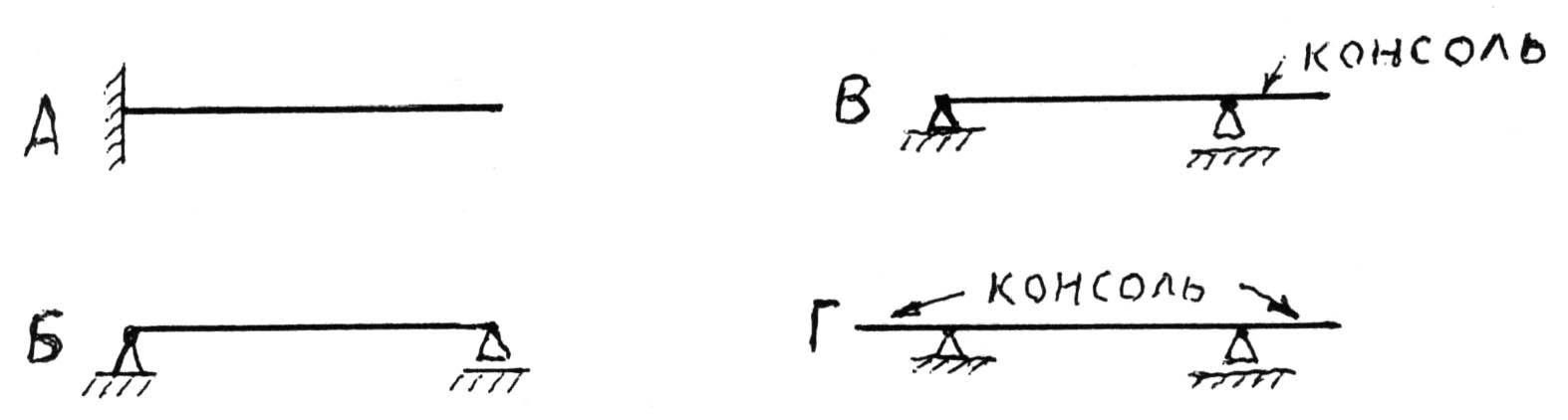
A - простая консоль; Б - двухопорная балка; В - двухопорная с одной консолью; Г - двухопорная с двумя консолями.

Поперечные силы и изгибающие моменты

При прямом поперечном изгибе два силовых фактора: поперечная сила и изгибающий момент Q_y и М_х (возникают касательные напряжения и нормальные); их вычисляют с помощью метода сечений через внешние силы, действующие на брус. Распределение поперечных сил и изгибающих моментов по длине бруса, а также нахождение предположительно опасных сечений производится с помощью эпюр поперечных сил и изгибающих моментов.

Брус (балку) изображают одной линией (при прямом поперечном изгибе все внешние силы лежат в одной плоскости и поэтому линия представляет продольную ось бруса). Опорные реакции определяют из 2 уравнений равновесия всей балки и считают известными. Применим метод сечений и рассмотрим условия равновесия левой отсечённой части - в сечении возникают два внутренних силовых фактора, заменяющих действие отброшенной части. В отброшенной части возникают такие же по значению, но противоположного направления поперечные силы и изгибающие моменты:

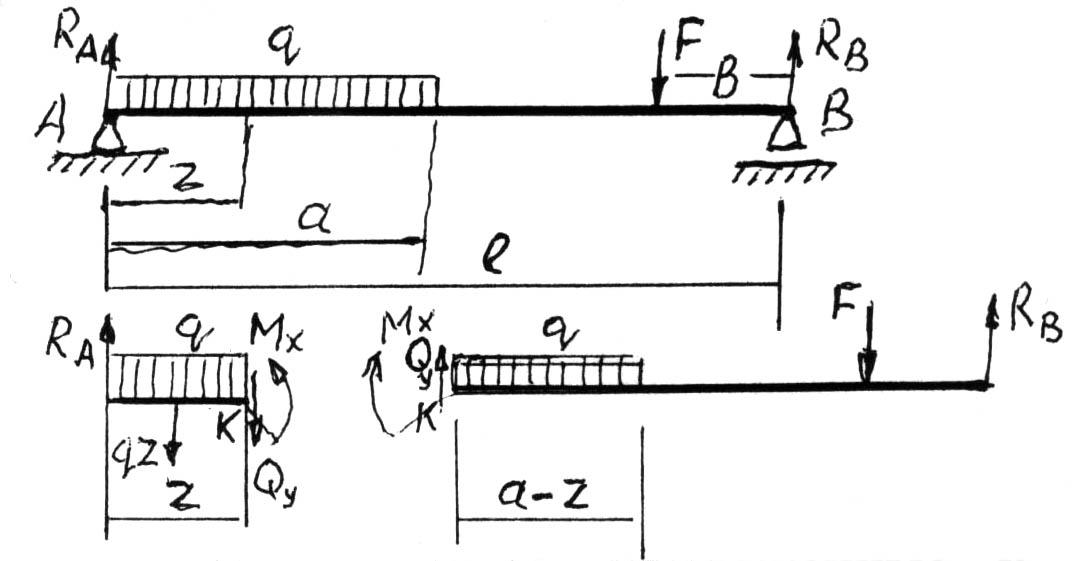
Внешние и внутренние силы, приложенные к оставленной части, образуют плоскую систему параллельных сил. Составляем уравнения равновесия: 1 - сумма проекций сил на направление параллельное силам; 2 -сумма моментов относительно точки проведения сечения

ΣY = 0, R_A - qz - Q_y = 0, откуда Q_y = R_A - qz.

ΣM_k = 0, R_Az - qz (z/2) - M_x = 0, откуда M_x = R_Az - qz²/2.

Итак, поперечная сила равна алгебраической сумме проекций внешних сил, приложенных к отсечённой части сил, на ось У; изгибающий момент равен сумме моментов внешних сил, приложенных к отсечённой части, относительно точки сечения К. При построении эпюр правило знаков:

Поперечные силы положительны, если стремятся повернуть элемент сечения по часовой стрелке; момент считается положительным, если элемент бруса изгибается выпуклостью вниз (сжатые волокна находятся в верхней части).

Для изгибающего момента знак «плюс» берётся, если элемент бруса изгибается выпуклостью вниз, а сжатые волокна находятся в верхней части. Положительные значения на эпюрах откладываются вверх от оси абсцисс. Практически удобнее устанавливать знаки Q_y и М_х удобнее определять по внешним силам (результаты обоих методов должны совпадать): внешняя сила, стремящаяся повернуть отсечённую часть по часовой стрелке относительно сечения, должна вызывать положительную поперечную силу. Знак момента определится, если отсечённую часть считать защемлённой в проведенном сечении: момент изгибающий эту часть положителен при выпуклости направленной вниз (сжатые волокна находятся сверху).