Задачи на кручение и сдвиг (срез и смятие)

В поперечном сечении только поперечная сила Q.

Касательные напряжения τ в поперечном сечении распределены равномерно по площади S_попер.

Если соединение осуществлено несколькими деталями (болты, штифты и т.д.) - все они нагружены одинаково.

Разрушение соединительных элементов происходит по площади сопряжения соединяемых деталей под действием напряжений среза τ_ср = .

Условие прочности

Расчетное τ_ср = ≤ [τ_ср], где Q - усилие на одну деталь, [τ_ср] - предельный допуск.

Q = , где ί - число болтов, к которым приложено внешнее усилие F.

[τ_ср] = (0,25 - 0,35) σ_т, где σ_т - предел текучести.

При недостаточной толщине соединяемых элементов σ_см - давление соединяющих деталей на стенки отверстия в соединяемых деталях, которые обминаются; σ_см - напряжение смятия.

Расчет предполагает равномерное распределение усилий по поверхности контакта, их перпендикулярность к поверхности контакта; если толщина соединяемых деталей недостаточна - стенки обминаются и деталь разрушается.

σ_см = ≤ [σ_см].

При разной толщине и материале ориентируются на меньшую прочность (более слабый материал).

При кручении в любой точке поперечного сечения τ перпендикулярен ρ и = и τ = и угол закручивания свободного конца φ =

Пример 1.

Ступенчатый стальной брус круглого поперечного сечения одним концом заделан и нагружен (рис.).

Построить: эпюры М_кр; τ_max и углов поворота поперечных сечений. Проверить прочность бруса при [τ_к] = 60 МПа; М₃ = 4 М; М₂ = 2 М; М₁ = М = 1кНм.

Решение:

1. Строим эпюру М от свободного конца (чтобы не определять реактивный момент в заделке). Аналогично построению эпюры продольных сил при растяжении (сжатии).

2. Строим эпюры τ_max

τ_max = , W_p = - жесткость сечения круглого бруса

(d₁ = 60; d₂ = 50; d₃ = 80 мм).

τ_{max AB} = = = + 23,6 МПа.

τ_{max BC} = - = + 40,8·10⁶ Па.

τ_{max CD} = + = - 40,8 МПа.

τ_{max DK} = + = 10 МПа.

τ_{max KL} = - = + 29,8 МПа.

Опасные сечения - участки BC и CD.

Материал используется нерационально τ_max  [τ_к] на 32%.

3. Строим эпюру углов поворота  (ее строим от защемленного конца; строим аналогично эпюре перемещения сечений при растяжении).

В пределах каждого участка линейная зависимость  = ₀z (длины участков указаны на рис. а = 400 мм). Поэтому вычисляем углы поворота граничных сечений участков: в точке K

_KL = = - = - 3,73·10^-3 рад.

G - модуль упругости II рода.

По справочнику G = 8·10⁴ МПа,

I_ρ = .

_DK = = 1,24·10^-3 рад.

Алгебраическая сумма _D = - (3,73 + 1,24)·10^-3 рад = - 2,49·10^-3 рад,

_C = 5,63·10^-3 рад,

_B = - 2,49·10^-3 рад,

_A = - 14,2·10^-3 рад.

Пример 2.

Вал диаметром d = 60 мм вращается с частотой n = 600 об/мин. Какова допускаемая мощность, если [τ_к] = 35 МПа и ₀ = 0,4 град/м.

Решение:

Из соображений прочности М = W_p [τ_к] = ·35·10⁶ = 1485 нм.

W_p = .

Из расчета на жесткость М = GI_ρ[₀] = 8·10¹⁰·· = 710 нм.

G - модуль упругости II рода из справочника для стали.

Выбираем меньшее и считаем мощность

P = М·ω = 710· = 44,6·10³ Вт = 44,6 кВт.

Пример 3.

Квадратная стальная пластина в горизонтальном направлении растягивается σ₁ = 120 МПа, в перпендикулярном направлении сжимается σ₂ = - σ₁. Определить касательную напряжения τ и изменение угла между диагоналями при Е = 2·10⁵ МПа, μ = 0,25.

Решение:

Так как σ₁ = - σ₂ у нас чистый изгиб, при этом, учитывая связь G и E, находим G = = 8·10⁴ МПа.

Относительный сдвиг γ = = = 1,5·10^-3,

на γ = tg α = α (рад) = 1,5·10^-3 рад·5,2′.

Пример 4.

Прямоугольная пластина растягивается напряжением G = 150 МПа, получая ε = 0,075%, ε′ = 0,025%. Каков модуль сдвига G и из какого материала она сделана?

Решение:

Для растяжения ε = , отсюда E = = = 2·10¹¹ Па.

Учитывая свойства материала μ = = 0,333

G = = = 7,5·10⁴ МПа.

Материал ищем по справочнику конструктора по значению G.

Пример 5.

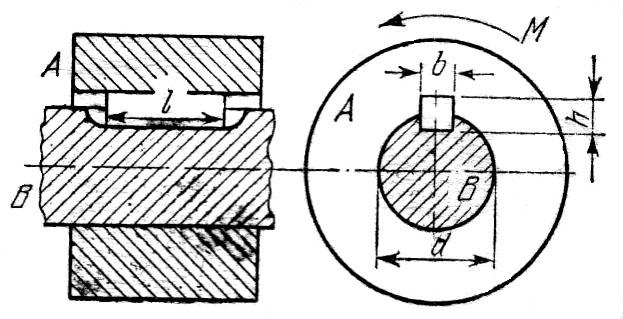
Деталь А закреплена на валу В с помощью шпонки 30×8×10 (ℓ×n×b). Диаметр детали D = 100 мм, вала d = 50 мм, для шпонки [τ_ср] = 80 МПа, [σ_см] = 200 МПа. Определить допускаемый момент [М], который можно с помощью шпонки передать от детали к валу.

Решение:

Передаваемый момент M = Ph = , откуда P = - сила давления детали на шпонку через момент, приложенный к детали, но с другой стороны P - предельное значение силы на срез шпонки,

т.е. [P_ср] = [τ] bℓ = 8·10⁷ Па ·3·10^-2·10^-2 м² = 24·10³ Н = 24 кН.

С другой стороны из условия прочности на смятие шпонки

[P_см] = [σ_см] = 2·10⁸ Па ·4·10^-3·3·10^-2 м² = 24·10³ Н = 24 кН.

В данной задаче [P]_срез= [P]_см и M = = 24 кН·25·10^-3 м = 0,6 кНм.

Пример 6.

Деталь А заканчивается 2 одинаковой толщины В проушинами, между которыми входит без зазора проушина детали В толщиной 2В. А и В соединены плотно входящим в отверстия проушин пальцем d = 20 мм. Исходя из прочности соединения на срез и смятие, определить силу Р, которую можно приложить к деталям при [τ]_{ср.пальца} = 80 МПа, [σ]_{см.пальца} = 240 МПа, а для деталей [σ]_см = 180 МПа, В = 8 мм.

Решение:

Палец срезается по 2 площадкам F_ср = = 6,28·10^-4 м².

Р_{ср.пальца} = [τ]_ср·F_ср = 80·10⁶ Па·6,28·10^-4 м² = 50·10³ Н.

Поверхность смятия проушин деталей А и В одинакова

F_см = 2Bd = 3,2 см² = 3,2·10^-4 м².

Для деталей σ_см < σ_{см. пальца}, поэтому усилие смятия считаем по меньшему

P = [σ_см]_дет·F_см = 1,8·10⁸ Па·3,2·10^-4 м² = 57,6 кН.

Определяющим будет срез, т.к. P_ср < P_см, т.е. [P] = 50 кН.

Пример 7.

Определить силу, необходимую для пробивки в стали толщиной S =10 мм отверстия d = 30 мм, τ_ср = 360 МПа.

Подобрать подходящий для изготовления пуансона материал.

Решение:

Усилие среза P_ср = τ_ср F,

F = S π d - боковая поверхность отверстия,

P_ср = 3,6·10⁸·3,14·30·10^-3·10·10^-3 = 338 кН.

Это усилие приложено ко всей площади поперечного сечения пуансона, следовательно σ_сж = = = 478 МПа.

[п] = 2÷5, следовательно σ_В = σ_сж = 1900 МПа.

По справочнику конструктора находим материал с таким пределом прочности Ст Х12.

Пример 8.

Тяга 1 соединена с вилкой 2 болтом (соединение без зазора) сила F = 48 кН, диаметр болта d = 20 мм, толщина тяги δ = 24 мм. Определить напряжения смятия тяги, напряжения среза в болте.

Решение:

А_см = dδ, σ_см = = = 100·10⁶ Па = 100 МПа.

Болт срезается по 2 плоскостям, т.е. А_ср = ,

τ_ср== = = МПа≈ 77МПа.

Пример 9.

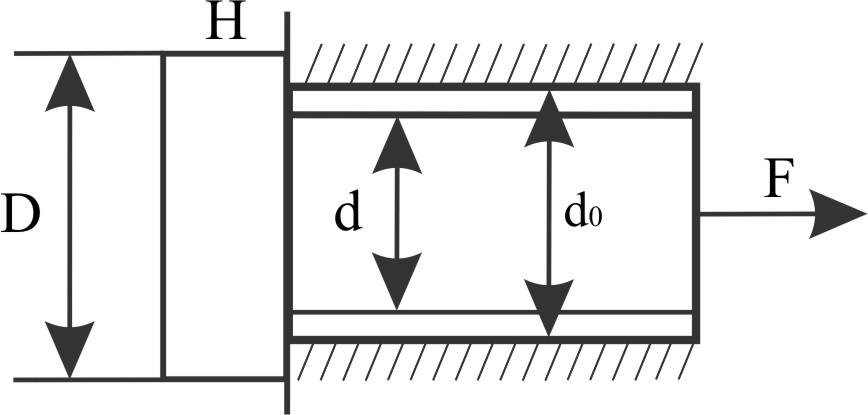
Определить диаметр D и высоту H головки стержня, нагруженного растягивающей силой F.

При расчете соблюсти равнопрочность стержня на растяжение и головки на срез, а ее опорной поверхности на смятие. Известно: [τ_ср] = 100 МПа, [σ_см] = 250 МПа, [σ_р] = 140 МПа, d = 32 мм, d₀ = 34 мм.

Решение:

1. [F_р]= [σ_р]· = 140·10⁶· = 112,6·10³ Н.

2. σ_см = ≤ [σ_см],

следовательно σ_см = ≤ [σ_см],

следовательно D≥ = =0,0417м= 41,7мм ≈42мм.

3. Срез головки.

τ_ср = ≤ [τ_ср], A_cр = πd₀H, следовательно τ_ср = ≤ [τ_ср],

следовательно H ≥ = = 0,01055 м = 10,55мм ≈11 мм.

Пример 10.

d = 24

d_ш = 20 δ₁ = 82

D = 40 δ₂ = 12

b₁ = 44 b₂ = 30

δ₃ = 24

Определить [F] при [τ_ср] = 80 МПа, [σ_см] = 210 МПа, [σ_р] = 120 МПа.

Решение:

Допускаемая нагрузка определяется по разному в разных местах:

тяг на растяжение в сечениях I и II N = [σ_р] A,

штыря на срез,

стенок отверстий в тягах на смятие,

краев проушины на срез, следовательно разное значение.

Выбираем наименьшую (обеспечит прочность всех элементов).

1. [F_р]_1-I = [σ_р]· = 120·10⁶· = 54,2·10³ Н (тяги 1 в сечении I).

2. [F_р]_2-II = [σ_р]·(b₁ - d_ш)·2 δ₁ = 120·10⁶·2·0,008·(0,044 - 0,02) = 46,1·10³ (тяги 1 в зоне проушин).

3. [F_р]_2-III = [σ_р] b₂ δ₂ = 120·10⁶·0,03·0,012 = 43,2·10³ (тяги 2 в сечении III).

4. [F_р]_2-II = [σ_р]·(D - d_ш) δ₂ = 28,8·10³ Н (тяги 2 в сечении II).

5. [F_ср]_шт = [τ_ср]·2 = 50,2·10³ Н.

6. [F_см]_{стенок тяги 1} = [σ_см]·2·δ₁ d_ш = 210·10⁶·2·8·20·10^-6 = 67,2·10³ Н.

[F_см]_{стенок тяги II} = [σ_см]·δ₂ d_ш = 210·10⁶·12·20·10^-6 = 50,4·10³ Н < [F_см]₁.

7. [F_вык]_{стенок тяги 1} = [τ_ср]·2е₁2 δ₁ = 80·10⁶·2·0,023·0,008·2 = 589·10³.

[F_вык]_{стенок тяги 2} = [τ_ср]·2е₂ δ₂ = 80·10⁶·2·0,02·0,012 = 38,4·10³ Н < [F_вык]₂.

Наименьшая 28,8·10³ Н. Необходимо изменить b₁, b₂, D, следовательно одинаковое значение F.

Пример 11.

Две пластины толщиной δ = 16 мм соединены с помощью накладок с двух сторон и заклепок диаметром d = 20 мм. Материал обладает следующими свойствами: [σ_с] = [σ_р] = 1600 ; [τ_ср] = 1000 , [σ_см] = 3200 . Определить необходимое количество заклепок при растягивающем усилии Р = 60 т.

Решение:

В данном случае заклепки - двухсрезные; поперечное сечение каждой

F = .

Поперечное усилие Q = τ_ср·F = (n^′ - число заклепок),

при смятии σ_см = ≤ [σ_см].

В нашем случае число срезов двухсрезных заклепок

n_ср = = = 17,4 ≈ 18, таким образом число заклепок с каждой стороны n_зак = = 9.

При рассмотрении смятия возможно:

I. F_см = d_зак·δ, если δ ≤ 2 δ_накл.

II. F_см = 2d_зак·δ_накл, если δ > 2 δ_накл и тогда [σ_см] = 2 [σ] и у нас рассмотрение смятия даст n^′′ = = = 5,85 ≈ 6.

Т.е., рассмотрение среза и смятия дают 2 ответа - 6 и 9 заклепок. По соображениям надежности берем большее число 9 (3 ряда по 3 заклепки с каждой стороны).

Осталось посчитать сечение соединяемых пластин.

F = = = 37,5 см², т.е. при толщине листа δ = 1,6 см чистая ширина листа b = = = 23,5 см.

К ней добавить ширину 3 отверстий под заклепки b^' = b + 3d = 29,5 см.

Толщину накладок выбираем δ_н = = 0,8 см.

Пример 12.

Технологически проще применить сварку (газовую или электродуговую) вместо заклепок. Заклепки заменяют сварочные швы.

Катет шва к = δ_накл, тогда толщина шва h = 0,7 к = 0,7 δ_накл.

На практике швы бывают торцовые и фланговые;

ширина накладки b_н = b_л - 2 δ_л.

Условие прочности: F_л ≤ F_накл = 2 b_накл·δ_накл, следовательно δ_н ≥ .

Пример 13.

Заклепочное соединение П10 заменить сварным и определить длину каждого флангового шва, приняв [τ_Э] = 1100 .

Решение:

Накладка будет иметь b_Н = b_л - 2 δ_л = 23,5 - 3,2 = 20,3 см.

Толщина накладки δ_н ≥ = = 0,92 см (δ_накл = К ≈ 1 см).

[P_фл] = ℓ_швов·0,7 к [τ_Э], откуда ℓ_швов = .

При двусторонних накладках швов 4 = 2_лев + 2_прав,

т.е. ℓ_фл.ш. = = 19,5 см.

Таким образом, одного флангового шва ℓ_{1 ш} = = 5 см.

Кроме технологической простоты - экономия металла на накладки и заклепки.