Модель Леонтьева многоотраслевой экономики

Основным инструментом построения и сохранения необходимых пропорций в многоотраслевой экономике является балансовый метод. Он состоит в том, что валовый выпуск i-ой отрасли должен быть равен сумме объемов продукции, потребляемой в производственной и непроизводственной сферах, т.е.

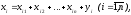(9)

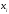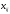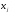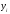где – общий (валовый) объем продукции i-ой отрасли, – объем продукции i-ой отрасли, потребляемый j-ой отраслью при производстве объема , – объем продукции i-ой отрасли, используемый в непроизводственной сфере (так называемый продукт конечного потребления).

Уравнения (9) называются соотношениями баланса.

Вводя коэффициенты 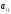– коэффициенты прямых материальных затрат по формуле:

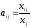
уравнение баланса можно записать в виде:

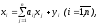(10)

или в более компактной (матричной) форме

X = АХ + Y, (11)

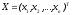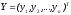где – вектор валового продукта, – вектор конечного продукта, 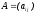– матрица прямых материальных затрат.

Уравнения (10), (11) называются уравнениями межотраслевого баланса или линейной моделью Леонтьева. Полученные уравнения баланса (10) можно использовать в двух направлениях:

1. по вектору конечного потребления определяют (планируют) необходимую величину валового выпуска каждой отрасли (основная задача);

2) по известному вектору валового выпуска X находят вектор конечного потребления Y:

У=X–AX=(Е–А)X. (12)

Пример. В таблице приведены данные об исполнении баланса между двумя видами отраслей за некоторый период.

Отрасль	Внутрипроизводственное потребление, ден. ед.			Конечный продукт		Валовый продукт
Энергетика	x11= 8	x12=20	y1=52		x1=80
Машиностроение	x21=12	x22=16	y2=72		x2=100

Вычислить: 1) величину конечного продукта, если вектор валового выпуска будет равен Х = (100,140)^т , 2) необходимый объем валового выпуска отраслей, если объем конечного потребления нужно увеличить до уровня Y = (100,150)^т.

Решение. Сначала, используя данные таблицы и формулу (2.10), составим матрицу прямых затрат

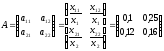
и затем построим матрицу полных затрат

1) Величину получающегося конечного продукта вычислим по формуле (2.12):

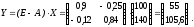
2) Матрица (Е–А) невырожденная, так как

.

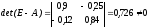Следовательно, для нее существует обратная матрица

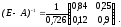
Из уравнения (12) получим

Таким образом, чтобы обеспечить конечный продукт в объеме Y = (100,150)^т, валовый выпуск в энергетической отрасли нужно поднять до 167,55 ден. ед., а в машиностроении – до 202,479 ден. ед..

Экономико-математическая модель линейного обмена

Эта модель иначе называется линейной моделью международной торговли. Ее исследование сводится к решению однородной системы линейных уравнений вида

где входящие величины имеют следующий смысл: 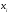– национальный доход страны 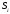, коэффициент 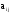выражает часть национального дохода страны 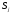, которая используется при товарообороте со страной 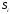. Матрица 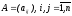называется структурной матрицей обмена (торговли), ее коэффициенты связаны соотношением:

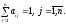
Пример. Структурная матрица трех стран 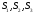имеет вид

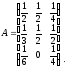
Каковы должны быть национальные доходы этих стран для того, чтобы торговля между ними была сбалансированной?

Решение. Соответствующая линейная модель торговли имеет вид

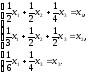
Решая эту систему уравнений методом Гаусса, получим X=(4,5α, 4α, α), где α – некоторая постоянная положительная величина, равная национальному доходу страны S3.