
- •Тема 1. Матричная алгебра План
- •Понятие матрицы. Виды матриц
- •Операции над матрицами и их свойства
- •I. Сложение матриц
- •II. Умножение матрицы на число
- •Свойства операций сложения и умножения на число:
- •III. Произведение матриц
- •Свойства операции умножения матриц:
- •IV. Транспонирование матриц
- •Свойства операции транспонирования:
- •Понятие определителя. Разложение определителя по элементам строки (столбца)
- •Свойства определителей
- •Базисный минор и ранг матрицы. Теорема о базисном миноре
- •Вычисление ранга матрицы методом окаймляющих миноров
- •Вычисление ранга матрицы с помощью элементарных преобразований
- •Обратная матрица и ее вычисление. Матричные уравнения
- •Свойства обратных матриц:
- •1) Если, то домножая обе части уравнения на слева, получим .
- •2) Если, то домножая обе части уравнения на справа, получим .
- •Использование алгебры матриц в экономике
- •Тема 2. Системы линейных уравнений План
- •Понятие системы линейных уравнений (слу)
- •Матричная форма записи слу
- •Условия совместности систем линейных уравнений. Теорема Кронекера–Капелли
- •Решение систем линейных уравнений методом обратной матрицы и по формулам Крамера
- •Метод Гаусса решения систем линейных уравнений
- •Однородные системы линейных уравнений
- •Фундаментальная система решений однородной системы линейных уравнений
- •Использование систем линейных уравнений в экономике
- •Модель Леонтьева многоотраслевой экономики
- •Экономико-математическая модель линейного обмена
- •Тема 3. Комплексные числа План
- •Понятие комплексного числа
- •Действия над комплексными числами
- •Тригонометрическая форма комплексного числа
- •Действия над комплексными числами в тригонометрической форме:
- •Тема 4. Элементы векторной алгебры План
- •Векторы на плоскости и в пространстве: основные понятия
- •Линейные операции над векторами
- •Свойства операций сложения векторов и умножения вектора на число
- •Координаты вектора на плоскости и в пространстве
- •Скалярное произведение векторов
- •Свойства скалярного произведения
- •Понятие линейного пространства
- •Примеры линейных пространств
- •Линейная зависимость и независимость системы n векторов
- •Примеры линейно зависимых и линейно независимых систем векторов
- •Базис. Координаты вектора в базисе
- •Матрица перехода к новому базису
- •Свойства матрицы перехода
- •Евклидово пространство: основные понятия
- •Выпуклые множества, свойства выпуклых множеств
- •Тема 5. Линейные отображения План
- •Понятие линейного оператора
- •Матрица линейного оператора
- •Действия над линейными операторами
- •Собственные векторы и собственные значения линейного оператора
- •Квадратичные формы
- •Критерий Сильвестра
Скалярное произведение векторов
Определение
14. Скалярным
произведением двух
векторов
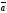 и
и
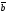 называется число равное произведению
длин этих векторов на косинус угла между
ними.
называется число равное произведению
длин этих векторов на косинус угла между
ними.
Скалярное
произведение обозначается
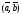 ,
или
,
или
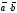 ,
или пишут просто
,
или пишут просто
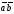 .
Таким образом, по определению
.
Таким образом, по определению
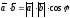 .
(8)
.
(8)
Замечание.
Под углом
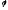 между векторами
между векторами
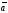 и
и
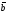 понимается наименьший из двух углов,
образуемых этими векторами при совмещении
их начал, т.е.
понимается наименьший из двух углов,
образуемых этими векторами при совмещении
их начал, т.е.
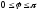 .
.
Иногда
для обозначения угла между векторами
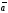 и
и
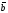 пишут
пишут
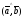 .
.
Замечание. В случае если один из векторов-сомножителей равен нулю, то скалярное произведение равно нулю.
Свойства скалярного произведения
1)
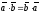 (коммутативность);
(коммутативность);
2)
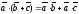 (дистрибутивность);
(дистрибутивность);
3)
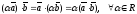 ;
;
4)
Скалярное произведение вектора на себя
равно квадрату его длины:
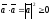 ;
;
5)
Скалярное произведение двух ненулевых
векторов равно нулю тогда и только
тогда, когда эти векторы перпендикулярны,
т.е.
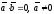 и
и
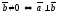 .
.
Замечание.
По аналогии с операцией умножения
на множестве чисел в случае скалярного
умножения вектора на себя будем писать
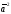 вместо
вместо
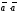 .
На практике удобно использовать формулу
для нахождения длины вектора, которая
легко получается из свойства 4:
.
На практике удобно использовать формулу
для нахождения длины вектора, которая
легко получается из свойства 4:
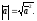 (9)
(9)
Определение
15. Два
ненулевых вектора
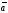 и
и
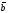 называются
ортогональными,
если их скалярное произведение равно
нулю.
называются
ортогональными,
если их скалярное произведение равно
нулю.
Теорема
3 (координатное представление скалярного
произведения).
Если
векторы
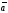 и
и
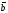 относительно базиса {
относительно базиса {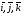 }
заданы своими координатами, т.е.
}
заданы своими координатами, т.е.
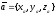 ,
,
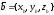 ,
то скалярное произведение векторов
,
то скалярное произведение векторов
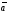 и
и
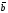 равно сумме произведений соответствующих
координат этих векторов, т.е.
равно сумме произведений соответствующих
координат этих векторов, т.е.
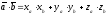 .
(10)
.
(10)
Следствие 1.
 .
(11)
.
(11)
Таким образом, длина вектора равна корню квадратному из суммы квадратов координат этого вектора.
Замечание.
Длина вектора
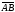 ,
где
,
где
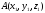 ,
,
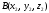 ,
находится по формуле
,
находится по формуле
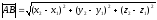 .
.
Следствие 2.
Косинус угла между ненулевыми векторами
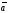 и
и
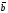 ,
заданными в базисе {
,
заданными в базисе {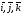 }
координатами
}
координатами
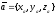 ,
,
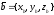 вычисляется по формуле
вычисляется по формуле
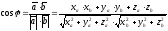 .
(12)
.
(12)
Замечание.
Косинусы
углов между вектором
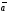 и координатными осями (базисными
векторами
и координатными осями (базисными
векторами
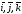 )
называются направляющими
косинусами вектора
)
называются направляющими
косинусами вектора
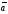 .
При подстановке координат векторов
.
При подстановке координат векторов
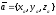 ,
,
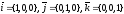 в формулу (12) получаются формулы для
нахождения направляющих косинусов
вектора
в формулу (12) получаются формулы для
нахождения направляющих косинусов
вектора
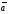
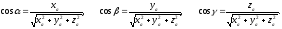 (13)
(13)
Возводя в квадрат обе части каждого из равенств (13) и складывая полученные результаты, находим
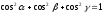 ,
(14)
,
(14)
т.е. сумма квадратов направляющих косинусов любого вектора равна единице.
Геометрический смысл скалярного произведения. Угол между двумя ненулевыми векторами острый (тупой), если скалярное произведение этих векторов есть число положительное (отрицательное). Угол между двумя ненулевыми векторами прямой, если скалярное произведение этих векторов равно нулю.
Это утверждение непосредственно следует из формулы (8) и свойств косинуса.
