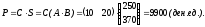Обратная матрица и ее вычисление. Матричные уравнения
Определение 25. Квадратная матрица называется невырожденной, если ее определитель отличен от нуля. В противном случае она называется вырожденной.
Определение
26. Обратной к
квадратной матрице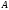
называется матрица
,
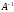которая удовлетворяет условию
.
(16)
Теорема 3. Матрица A тогда и только тогда имеет обратную матрицу, когда она невырожденная.
Доказательство.
Достаточность.
Для матрицы
;
,
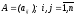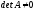составим матрицу
из алгебраических дополнений и затем
транспонируем ее. Получившуюся в
результате матрицу обозначим
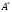и назовем присоединенной
(или союзной) к
A.
Иными словами,
где
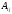– алгебраическое дополнение элемента
.
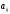Вычисляя
произведения
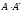и
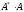матриц, с учетом теоремы 1 получим
.
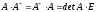Разделив последнее
соотношение на величину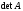
,
имеем:
откуда c
учетом равенств (16), (10), найдем:
.
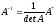Мы получили формулу нахождения обратной
матрицы и, следовательно, доказали ее
существование.
Таким образом, формула для вычисления обратной матрицы имеет вид:
(17)
Замечание.
Для каждой невырожденной матрицы А
существует единственная обратная
матрица
.
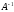Существует еще
один способ нахождения обратной матрицы
при помощи элементарных преобразований.
Этот способ состоит в следующем:
составляется матрица размера
,
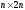при помощи приписывания к матрице A
справа единичной матрицы. Элементарными
преобразованиями строк преобразуют
полученную матрицу так, чтобы обратить
ее левую половину в единичную матрицу.
Тогда справа получится матрица
.
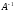Свойства обратных матриц:
1.
.
Непосредственно следует из равенства 16.
2.
.
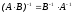Доказательство.
.
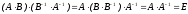Следовательно, матрицы
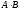и
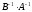обратные по отношению друг к другу, т.
е.
.
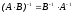3.
.
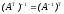Доказательство.
Из соотношения
16:
.
По свойству 4 операции транспонирования
.
Следовательно, матрицы
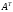и
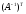взаимообратные, т. е.
.
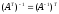Определение 27. Простейшими матричными уравнениями будем называть уравнения следующих трех типов:
,
,
,
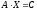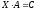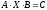(18)
где
,
,
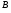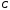– некоторые числовые матрицы, а
–
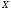неизвестная матрица, которую нужно
найти.
Под решением матричного уравнения будем понимать матрицу X, которая обращает матричное уравнение в тождество.
Искать решение матричных уравнений будем с помощью обратных матриц в зависимости от типа уравнения следующими тремя способами:
1) Если, то домножая обе части уравнения на слева, получим .
2) Если, то домножая обе части уравнения на справа, получим .
3) Есл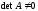и
и
,
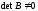то домножая уравнение
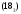на
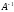слева и на
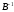справа, получим
.
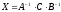Использование алгебры матриц в экономике
Понятие матрицы часто используется в практической деятельности. Например, данные о выпуске продукции нескольких видов в каждом квартале года или нормы затрат нескольких видов ресурсов на производство продукции нескольких типов и т. д. удобно записать в виде матриц.
Пример. Предприятие выпускает продукцию трех видов P1, P2, P3 и для их производства использует сырье двух видов. Нормы расхода сырья, стоимость единицы сырья и план выпуска продукции приведены в таблице.
|
Вид сырья |
Виды продукции |
Стоимость сырья |
|||
|
Р1 |
P2 |
P3 |
|
||
|
1 |
1 |
4 |
2 |
10 |
|
|
2 |
2 |
5 |
3 |
20 |
|
|
План выпуска продукции |
50 |
30 |
40 |
|
|
Определить расход сырья, необходимый для выполнения плана выпуска продукции, а также общую стоимость сырья.
Решение. Введем матрицы:
где А – технологическая матрица, элементы которой выражают норму расхода сырья для производства каждой единицы продукции, В – матрица-план выпуска продукции, С – матрица-стоимость единицы каждого типа сырья. Тогда общий расход сырья S можно выразить матричным произведением:
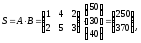
что в денежном выражении составит
