Примеры линейно зависимых и линейно независимых систем векторов
Теоремы 1, 2, а также свойства 1–2 линейно зависимых систем векторов позволяют сформулировать следующие утверждения:
1. Система, состоящая из одного вектора, линейно зависима тогда и только тогда, когда он нулевой.
2. Система, состоящая из двух векторов, линейно зависима, тогда и только тогда, когда векторы коллинеарны.
3. Система, состоящая из трех векторов, линейно зависима, тогда и только тогда, когда данные три вектора компланарны.
Теорема 4.
Пусть в пространстве
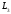даны три некомпланарных вектора
,
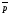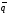и
,
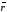тогда любой вектор
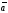этого пространства можно разложить по
данным векторам, причем единственным
образом, т.е.
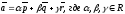
Следствие.
Любые четыре
(или более) вектора пространства
линейно зависимы.
Базис. Координаты вектора в базисе
Рассмотрим понятие базиса для произвольного линейного пространства L.
Определение
4.21. Базисом линейного пространства
L называется любая
упорядоченная система линейно независимых
векторов
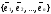этого пространства таких, что каждый
вектор
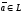представим в виде линейной комбинации
этих векторов, т.е.
,
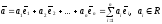(16)
Выражение (16)
называется разложением вектора
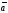по базису
,
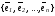а коэффициенты в разложении {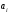
}(
)
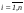называются координатами вектора
относительно данного базиса.
Замечание.
Каждому вектору
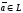ставится в соответствие единственный
набор чисел {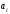
}(
)
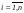и наоборот, т.е. координаты вектора
относительно базиса определяются
однозначно.
Таким образом,
вектор можно задавать его координатами:
.
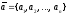Такой вектор называется n-мерным арифметическим вектором или просто n-мерным вектором. Название «n-мерный вектор» связано с тем, что при n=2 или n=3 получаем координаты вектора на плоскости или в пространстве.
Замечание. Коэффициенты одного и того же вектора в разложениях по разным базисам различны.
Замечание.
Координаты вектора
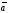можно также записывать в виде строчной
или столбцевой
матриц. Поэтому очень часто под вектором
понимают соответствующую сточную
(столбцевую) матрицу и наоборот: при
необходимости любую матрицу рассматривают
как вектор с соответствующими координатами.
Строчные
(столбцевые)
матрицы часто
называют
вектор-строкой
(вектор-столбцом).
В пространстве
L существует много
различных базисов, однако все они состоят
из одного и того же числа векторов.
Количество векторов в базисе называется
размерностью линейного пространства.
Размерность линейного пространства L
будем обозначать dim
L (от французского
слова dimension – размерность).
Пространство L
размерности n будем
называть n-мерным
и писать
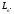
Если пространство состоит из одного нулевого элемента, то его размерность будем считать равной нулю.
Замечание. Из
определения базиса 21 и теорем 1, 2 и 4
следует: 1) базисом векторов на
прямой является любой ненулевой
вектор
,
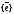лежащий на этой прямой; 2) базисом
векторов на плоскости является любая
упорядоченная пара неколлинеарных
векторов
,
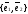принадлежащих этой плоскости; 3) базисом
векторов в трехмерном пространстве
является любая упорядоченная тройка
некомпланарных векторов
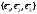этого пространства. Такие базисы называют
аффинными базисами векторов
прямой, плоскости и трехмерного
пространства соответственно. Множество
векторов прямой образует одномерное,
плоскости — двумерное, обычного
пространства — трехмерное векторные
пространства. Выше мы обозначили их
через
соответственно. Здесь нижний индекс
означает размерность пространства.
Пространства, в которых нельзя указать базис, состоящий из конечного числа векторов, называются бесконечномерными. Примером бесконечномерного пространства может служить множество С [a, b] непрерывных на отрезке [a, b] функций f(t), для которых операции сложения и умножения на число определены естественным образом.
В дальнейшем мы будем рассматривать конечномерные векторные пространства.