Однородные системы линейных уравнений

Рассмотрим систему линейных однородных уравнений:

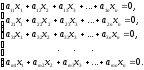(8)

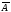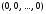Система (8) является частным случаем системы (1). Она всегда совместна. С одной стороны, это вытекает из теоремы Кронекера–Капелли, так как матрица получена из А добавлением нулевого столбца и, следовательно, ранги этих матриц равны. С другой стороны, это видно и непосредственно, так как ей всегда удовлетворяет решение , которое будем называть нулевым, или тривиальным. Иногда система (8), кроме тривиального, может иметь и другие решения (нетривиальные).

Пусть матрица А системы (8) имеет ранг .

Система линейных однородных уравнений (8) тогда и только тогда имеет единственное нулевое решение, когда ранг ее матрицы равен количеству неизвестных,

т. е. r=n.

Для того чтобы система (8) имела нетривиальные решения, необходимо и достаточно, чтобы ранг матрицы системы был меньше числа неизвестных, т. е. r<n.

Все нетривиальные решения системы можно найти, решая систему методом Гаусса.

Замечание. В матрице 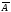однородной системы (8) нулевой столбец свободных членов писать не будем. Поэтому вместо матрицы 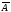будем писать матрицу А.

Фундаментальная система решений однородной системы линейных уравнений

Пусть 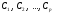– вектор-решения системы (8), а 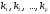– некоторые числа. Тогда выражение вида 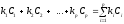называется линейной комбинацией вектор-решений системы.

Определение 9. Вектор-решения 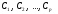называются линейно зависимыми, если хотя бы одно из них является линейной комбинацией остальных. В противном случае, вектор-решения называются линейно независимыми.

Вектор-решения системы линейных однородных уравнений обладает следующими свойствами.

Лемма 1. Любая линейная комбинация конечного числа вектор-решений системы однородных линейных уравнений (8) также является вектор-решением данной системы.

В этом несложно убедиться непосредственной подстановкой линейной комбинации вектор-решений в систему.

Лемма 2. Пусть для системы линейных однородных уравнений (8) 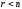, где r – ранг матрицы системы, а n – число неизвестных. Тогда эта система имеет (n–r) линейно независимых вектор-решений таких, что любое другое решение этой системы является их линейной комбинацией.

Замечание. Можно показать, что (n–r) – максимальное число линейно независимых вектор-решений системы.

Определение 10. Максимальный набор линейно независимых решений однородной системы называется фундаментальной системой решений.

На практике мы будем искать нормированную фундаментальную систему решений.

Правило нахождения нормированной фундаментальной системы решений: для нахождения нормированной фундаментальной системы решений однородной системы с n неизвестными ранга r (r<n) нужно в общее решение системы в качестве значений свободных переменных подставить строки (столбцы) единичной матрицы .

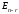Использование систем линейных уравнений в экономике

Рассмотрим несколько прикладных задач, которые приводятся к решению систем линейных уравнений.

Пример. Для производства трех видов изделий Р₁, P₂ и P₃ предприятие использует три вида сырья: S₁, S₂ и S₃. Необходимые технологические характеристики приведены в таблице.

Вид сырья	Расход сырья по видам изделий, вес.ед./изд.				Запасы сырья
	Р1	P2	P3
S1 S2 S3	5 3 6	3 6 4	4 2 3	1160 1160 1260

Требуется составить план выпуска изделий при известных запасах сырья.

Решение. Пусть x₁, x₂ , x₃ – неизвестные объемы выпуска каждого вида изделий. Предполагая, что при производстве изделий используются все запасы сырья, составим балансовые соотношения в виде системы трех уравнений:

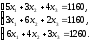
Определитель 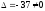. Следовательно, система имеет единственное решение, которое найдем по формулам Крамера:

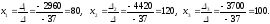
Пример. Общая задача о прогнозе выпуска продукции может быть поставлена и решена следующим образом.

Пусть 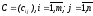– технологическая матрица расхода сырья m видов, использующегося для выпуска продукции n видов, т.е. коэффициент 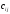выражает норму расхода i-го сырья для производства единицы продукции j-го вида. Если, кроме того, известен вектор запаса сырья 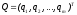, то при условии использования всего сырья вектор-план выпуска продукции 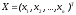находится из системы уравнений

Решение. Если матрица С имеет обратную (т.е. m=n=rangC), то решение задачи единственно:

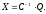
Если же 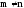, например m<n, то система, если она имеет решение, разрешима неоднозначно. Чтобы система и в этом случае имела единственное решение, на систему приходится накладывать дополнительные условия. В частности, добавляют условие необходимости нахождения оптимального решения.

Пример. Две ткацкие фабрики получают станки с двух заводов. Запасы станков, произведенных заводами, потребности фабрик в станках, а также стоимость их перевозки к потребителям известны и приведены в таблице.

Заводы	Потребители и стоимость перевозки			Запасы заводов
	П1	П2
1 2	8 10	12 15	130 170
Потребность фабрик	120	180	300

Найти оптимальный план поставок станков потребителям, если минимальные перевозки составляют 3510 ден. ед.

Решение. Введем переменные 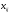, выражающие количество станков, поставляемых i-м заводом j-й фабрике. Так как все станки, произведенные заводами, вывозятся, то соответствующие балансовые соотношения запишутся в виде системы пяти уравнений с четырьмя неизвестными.

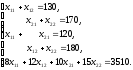
_{Решая составленную систему уравнений методом Гаусса, получим, что}