Действия над линейными операторами

Введем арифметические действия над линейными операторами:

1. Суммой линейных операторов 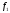и 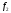называется оператор 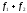, который действует по следующему правилу: .

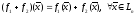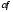2. Произведением оператора f на число называется оператор , который действует по следующему правилу: .

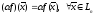3. Произведением оператора 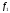на оператор 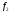называется оператор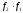, который действует по следующему правилу: .

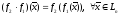Все введенные операторы являются линейными. Покажем, например, что оператор произведения линеен.

Действительно, для и имеем

.

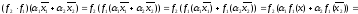
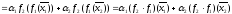Если относительно базиса операторы f, 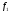и 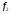задаются матрицами А, 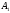и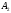, то несложно показать, что матрица суммы 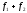опе­раторов равна сумме 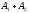матриц этих операторов; мат­рица произведения оператора f на число 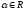равна произ­ведению 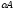матрицы оператора на это число; матрица произ­ведения операторов равна произведению 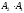матриц этих операторов.

Собственные векторы и собственные значения линейного оператора

Пусть 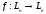– линейный оператор, действующий в пространстве .

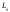Определение 5. Ненулевой вектор 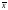называется собствен­ным вектором линейного оператора f, если для этого вектора

(3)

где λ – некоторое число, называемое собственным значением линейного оператора , соответствующим вектору .

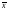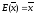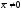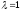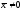Для единичного оператора любой вектор является собственным вектором, относящимся к единственному собственному значению . Для нулевого оператора любой вектор является собственным вектором, относящимся к единственному собственному значению .

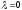Решим задачу нахождения собственных векторов.

Формулу (3) с учетом (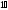) можно переписать в матричном виде:

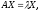
или

()

где E – единичная матрица порядка n.

Подробная запись формулы () имеет вид:

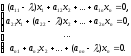(4)

Решая однородную систему уравнений (4), находим координаты собственного вектора 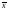при данном собственном зна­чении λ.

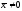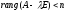Так как , то , а это значит, что 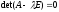, т. е.

(5)

Уравнение (5) называется характеристическим уравне­нием матрицы А или оператора f.

Таким образом, собственные значения 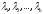линейного оператора 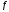находятся из уравнения (5), а координаты соответствующих собствен­ных векторов – из системы уравнений (4).

Можно доказать, что если собственные числа оператора f различны, то соот­ветствующие им собственные векторы линейно независимы.

Квадратичные формы

Определение 6. Квадратичной формой 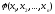от n переменных называется сумма, каждый член которой является или квадратом одной из переменных, или произведением двух различных переменных, взятых с некоторым коэффициентом, т.е.

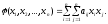(6)

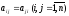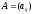Действительные числа называются коэффициентами квадратичной формы, причем , а матрица , составленная из этих коэффициентов, называется матрицей квадратичной формы. Ранг матрицы А называется рангом квадратичной формы.

Квадратичная форма в матричной записи имеет вид:

()

где 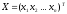– столбцевая матрица, составленная из переменных.

Действительно,

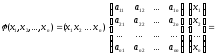
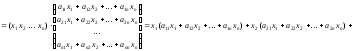
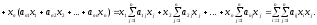
Пусть некоторый невырожденный линейный оператор f переводит вектор в вектор 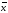. Так как действие линейного оператора на вектор сводится к умножению некоторой матрицы В линейного оператора на столбцевую матрицу , то имеем: 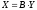. Выясним, как изменится матрица квадратичной формы при линейном невырожденном преобразовании переменных. Квадратичная форма примет вид:

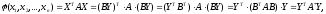
где .

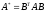_{Таким образом, при невырожденном линейном преобразовании 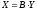матрица} квадратичной формы будет иметь вид: .

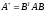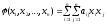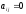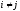Определение 7. Квадратичная форма называется канонической (канонического вида), если все коэффициенты при , т.е.

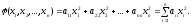
Другими словами, канонический вид квадратичной формы – это координатная запись формы, не содержащая слагаемых вида 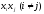, а содержащая только квадраты координат.

Матрица канонической квадратичной формы является диагональной:

Теорема 6. Невырожденное линейное преобразование переменных приводит к каноническому виду любую квадратичную форму.

Канонический вид квадратичной формы определяется неоднозначно, одна и та же квадратичная форма может быть приведена к каноническому виду многими способами. Полученные различными способами канонические формы обладают рядом общих свойств:

1. Закон инерции квадратичных форм: число положительных, число отрицательных и число ненулевых коэффициентов при квадратах переменных в канонической форме не зависит от способа приведения квадратичной формы к этому виду.

2. Свойство ранга: ранг квадратичной формы равен количеству ненулевых коэффициентов при квад­ратах переменных в каноническом виде формы и не изменяется при линейных преобразованиях.

Определение 8. Квадратичная форма 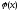называется положительно определенной, если для любого ненулевого вектора выполняется неравенство .

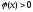Определение 9. Квадратичная форма 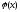называется неотрицательно определенной, или положительно полуопределенной, если для любого ненулевого вектора выполняется неравенство .

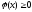Аналогично определяется отрицательно определенная и неположительно определенная (отрицательно полуопределенная) квадратичная форма.

Остальные квадратичные формы, не относящиеся к определенным, называются неопределенными или знакопеременными квадратичными формами.

Теорема 7 (об определении знака формы по собственным числам). Для того, чтобы квадратичная форма была положительно (отрицательно) определенной, необходимо и достаточно, чтобы все собственные числа матрицы квадратичной формы были положительными (отрицательными).