
- •Тема 1. Матричная алгебра План
- •Понятие матрицы. Виды матриц
- •Операции над матрицами и их свойства
- •I. Сложение матриц
- •II. Умножение матрицы на число
- •Свойства операций сложения и умножения на число:
- •III. Произведение матриц
- •Свойства операции умножения матриц:
- •IV. Транспонирование матриц
- •Свойства операции транспонирования:
- •Понятие определителя. Разложение определителя по элементам строки (столбца)
- •Свойства определителей
- •Базисный минор и ранг матрицы. Теорема о базисном миноре
- •Вычисление ранга матрицы методом окаймляющих миноров
- •Вычисление ранга матрицы с помощью элементарных преобразований
- •Обратная матрица и ее вычисление. Матричные уравнения
- •Свойства обратных матриц:
- •1) Если, то домножая обе части уравнения на слева, получим .
- •2) Если, то домножая обе части уравнения на справа, получим .
- •Использование алгебры матриц в экономике
- •Тема 2. Системы линейных уравнений План
- •Понятие системы линейных уравнений (слу)
- •Матричная форма записи слу
- •Условия совместности систем линейных уравнений. Теорема Кронекера–Капелли
- •Решение систем линейных уравнений методом обратной матрицы и по формулам Крамера
- •Метод Гаусса решения систем линейных уравнений
- •Однородные системы линейных уравнений
- •Фундаментальная система решений однородной системы линейных уравнений
- •Использование систем линейных уравнений в экономике
- •Модель Леонтьева многоотраслевой экономики
- •Экономико-математическая модель линейного обмена
- •Тема 3. Комплексные числа План
- •Понятие комплексного числа
- •Действия над комплексными числами
- •Тригонометрическая форма комплексного числа
- •Действия над комплексными числами в тригонометрической форме:
- •Тема 4. Элементы векторной алгебры План
- •Векторы на плоскости и в пространстве: основные понятия
- •Линейные операции над векторами
- •Свойства операций сложения векторов и умножения вектора на число
- •Координаты вектора на плоскости и в пространстве
- •Скалярное произведение векторов
- •Свойства скалярного произведения
- •Понятие линейного пространства
- •Примеры линейных пространств
- •Линейная зависимость и независимость системы n векторов
- •Примеры линейно зависимых и линейно независимых систем векторов
- •Базис. Координаты вектора в базисе
- •Матрица перехода к новому базису
- •Свойства матрицы перехода
- •Евклидово пространство: основные понятия
- •Выпуклые множества, свойства выпуклых множеств
- •Тема 5. Линейные отображения План
- •Понятие линейного оператора
- •Матрица линейного оператора
- •Действия над линейными операторами
- •Собственные векторы и собственные значения линейного оператора
- •Квадратичные формы
- •Критерий Сильвестра
Выпуклые множества, свойства выпуклых множеств
Рассмотрим
n-мерное
евклидово пространство
 .
.
В пространстве
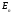 наряду с векторами можно рассматривать
также точки. Под точкой n-мерного
евклидова пространства
наряду с векторами можно рассматривать
также точки. Под точкой n-мерного
евклидова пространства
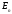 будем понимать вектор с началом в начале
координат.
будем понимать вектор с началом в начале
координат.
Определение 26. Множество точек n-мерного евклидова пространства называется выпуклым, если, наряду с любыми двумя его точками, содержится и весь отрезок.
Теорема
5.
Точка X
тогда и только
тогда является точкой отрезка с концами
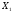 и
и
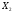 ,
когда выполняется условие
,
когда выполняется условие
 где
где
 .
.
Тема 5. Линейные отображения План
Линейные операторы: основные понятия, свойства. Собственные векторы и собственные значения линейного оператора. Понятие квадратичной формы. Приведение квадратичной формы к каноническому виду. Критерий знакоопределенности квадратичной формы.
Понятие линейного оператора
Пусть
 и
и
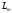 – линейные пространства размерности
n и m.
– линейные пространства размерности
n и m.
Определение
1. Отображением линейного
пространства
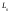 в линейное пространство
в линейное пространство
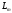 называется правило f,
по которому каждому элементу
называется правило f,
по которому каждому элементу
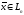 ставится в соответствие единственный
элемент
ставится в соответствие единственный
элемент
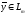 .
Обозначают:
.
Обозначают:
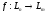 или
или
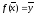 .
.
Вектор
 называется образом вектора
называется образом вектора
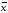 при отображении
при отображении
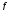 ,
а вектор
,
а вектор
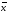 – прообразом вектора
– прообразом вектора
 .
.
Определение
2. Отображение
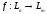 называется линейным, если оно
сохраняет линейные операции над
векторами, т.е. выполняются следующие
соотношения:
называется линейным, если оно
сохраняет линейные операции над
векторами, т.е. выполняются следующие
соотношения:
1.
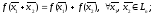
2.

Будем рассматривать
линейные отображения
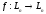 .
Такие отображения называются линейными
операторами (линейными преобразованиями).
.
Такие отображения называются линейными
операторами (линейными преобразованиями).
Определение
3.
Линейный
оператор называется тождественным
или единичным,
если он преобразует любой вектор
 в самого себя. Он обозначается E,
т.е.
в самого себя. Он обозначается E,
т.е.
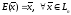 .
.
Определение
4.
Линейный
оператор называется нулевым,
если он преобразует любой вектор
 в нулевой
вектор
в нулевой
вектор
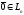 .
Он обозначается O,
т.е.
.
Он обозначается O,
т.е.
 .
.
Матрица линейного оператора
Пусть в
векторном пространстве
 задан базис
задан базис
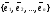 ,
запишем разложение вектора
,
запишем разложение вектора
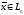 по данному базису:
по данному базису:

В
силу того, что оператор
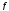 –
линейный, имеем:
–
линейный, имеем:
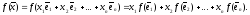
Так
как
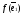 ,
,
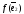 ,
…,
,
…,
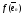 тоже являются векторами пространства
тоже являются векторами пространства
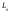 ,
то их также можно разложить по базису,
т. е. представить в виде:
,
то их также можно разложить по базису,
т. е. представить в виде:
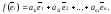
Таким
образом,
 окончательно можно представить в виде:
окончательно можно представить в виде:
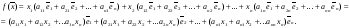
С
другой стороны, вектор
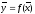 можно также разложить по базису
можно также разложить по базису
 :
:
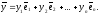
В
силу однозначности разложения вектора
 по базису, имеем:
по базису, имеем:
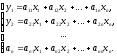
Система уравнений в матричной форме имеет вид:
 (1)
(1)
или в сокращенной матричной форме
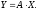 (
(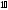 )
)
Таким образом,
действие линейного оператора на вектор
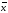 сводится к умножению некоторой матрицы
сводится к умножению некоторой матрицы
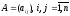 на столбцевую
матрицу X,
составленную из координат вектора
на столбцевую
матрицу X,
составленную из координат вектора
 .
Матрица А
называется матрицей
линейного оператора
в базисе
.
Матрица А
называется матрицей
линейного оператора
в базисе
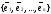 ,
а ранг матрицы А
– рангом
оператора.
Порядок матрицы А
совпадает с размерностью пространства.
Матрица линейного оператора полностью
характеризует линейный оператор.
,
а ранг матрицы А
– рангом
оператора.
Порядок матрицы А
совпадает с размерностью пространства.
Матрица линейного оператора полностью
характеризует линейный оператор.
Если матрица А невырожденная, то линейный оператор (линейное преобразование переменных) называется невырожденным.
Справедлива следующая
Теорема
5. Различным линейным операторам
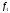 и
и
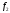 ,
действующим в n- мерном
векторном, соответствуют различные
матрицы в базисе. Любая квадратная
матрица А порядка n
является матрицей некоторого линейного
оператора, действующего в линейном
пространстве.
,
действующим в n- мерном
векторном, соответствуют различные
матрицы в базисе. Любая квадратная
матрица А порядка n
является матрицей некоторого линейного
оператора, действующего в линейном
пространстве.
Пусть
в
векторном пространстве
 заданы
«старый»
заданы
«старый»
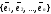 и «новый»
и «новый»
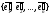 базисы. При переходе от старого базиса
базисы. При переходе от старого базиса
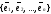 к новому базису
к новому базису
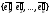 пространства
пространства
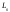 матрица линейного оператора f
изменяется, т.е. если А
и
матрица линейного оператора f
изменяется, т.е. если А
и
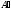 –
матрицы
линейного
оператора f
в старом
и новом
базисах, то они связаны соотношением:
–
матрицы
линейного
оператора f
в старом
и новом
базисах, то они связаны соотношением:
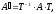 (
(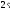 )
)
где Т – матрица перехода от старого базиса к новому.
Замечание.
При переходе
от старого базиса к новому определитель
матрицы сохраняет свою величину, т.е.
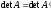 .
.
