
- •Тема 1. Матричная алгебра План
- •Понятие матрицы. Виды матриц
- •Операции над матрицами и их свойства
- •I. Сложение матриц
- •II. Умножение матрицы на число
- •Свойства операций сложения и умножения на число:
- •III. Произведение матриц
- •Свойства операции умножения матриц:
- •IV. Транспонирование матриц
- •Свойства операции транспонирования:
- •Понятие определителя. Разложение определителя по элементам строки (столбца)
- •Свойства определителей
- •Базисный минор и ранг матрицы. Теорема о базисном миноре
- •Вычисление ранга матрицы методом окаймляющих миноров
- •Вычисление ранга матрицы с помощью элементарных преобразований
- •Обратная матрица и ее вычисление. Матричные уравнения
- •Свойства обратных матриц:
- •1) Если, то домножая обе части уравнения на слева, получим .
- •2) Если, то домножая обе части уравнения на справа, получим .
- •Использование алгебры матриц в экономике
- •Тема 2. Системы линейных уравнений План
- •Понятие системы линейных уравнений (слу)
- •Матричная форма записи слу
- •Условия совместности систем линейных уравнений. Теорема Кронекера–Капелли
- •Решение систем линейных уравнений методом обратной матрицы и по формулам Крамера
- •Метод Гаусса решения систем линейных уравнений
- •Однородные системы линейных уравнений
- •Фундаментальная система решений однородной системы линейных уравнений
- •Использование систем линейных уравнений в экономике
- •Модель Леонтьева многоотраслевой экономики
- •Экономико-математическая модель линейного обмена
- •Тема 3. Комплексные числа План
- •Понятие комплексного числа
- •Действия над комплексными числами
- •Тригонометрическая форма комплексного числа
- •Действия над комплексными числами в тригонометрической форме:
- •Тема 4. Элементы векторной алгебры План
- •Векторы на плоскости и в пространстве: основные понятия
- •Линейные операции над векторами
- •Свойства операций сложения векторов и умножения вектора на число
- •Координаты вектора на плоскости и в пространстве
- •Скалярное произведение векторов
- •Свойства скалярного произведения
- •Понятие линейного пространства
- •Примеры линейных пространств
- •Линейная зависимость и независимость системы n векторов
- •Примеры линейно зависимых и линейно независимых систем векторов
- •Базис. Координаты вектора в базисе
- •Матрица перехода к новому базису
- •Свойства матрицы перехода
- •Евклидово пространство: основные понятия
- •Выпуклые множества, свойства выпуклых множеств
- •Тема 5. Линейные отображения План
- •Понятие линейного оператора
- •Матрица линейного оператора
- •Действия над линейными операторами
- •Собственные векторы и собственные значения линейного оператора
- •Квадратичные формы
- •Критерий Сильвестра
Матрица перехода к новому базису
Пусть
в n-мерном
векторном пространстве
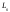 даны два различных базиса:
даны два различных базиса: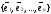 и
и
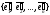 ,
которые условимся называть «старым» и
«новым» базисами пространства. Каждый
из векторов нового базиса можно выразить
через векторы старого базиса:
,
которые условимся называть «старым» и
«новым» базисами пространства. Каждый
из векторов нового базиса можно выразить
через векторы старого базиса:
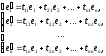
а так же записать в матричной форме:
 (17)
(17)
или в сокращенной матричной форме:
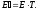 (17
(17 )
)
Матрица

называется матрицей перехода от старого базиса к новому базису.
Замечание. Следует обратить внимание на то, что координаты векторов нового базиса по старому базису располагаются в матрице перехода по столбцам.
Формулы
(16) и (16 )
называются формулами
преобразования базиса.
)
называются формулами
преобразования базиса.
Свойства матрицы перехода
1) Матрица
перехода является невырожденной, т.е.
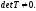
2) Матрица перехода
от нового базиса к старому базису имеет
вид
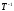 .
Действительно, умножив равенство (16
.
Действительно, умножив равенство (16 )
справа на матрицу
)
справа на матрицу
 ,
получим
,
получим
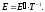
Найдем зависимость между координатами вектора в разных базисах.
Пусть
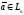 имеет координаты
имеет координаты
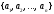 в старом базисе и
в старом базисе и
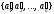 в
новом базисе, тогда
в
новом базисе, тогда

Подставив
в это выражение разложение векторов
 по базису
по базису
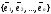 ,
получим
,
получим
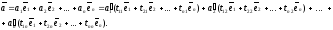
В силу однозначности разложения вектора по базису, имеем
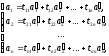
или в матричной форме:
 (18)
(18)
или в сокращенной матричной форме:
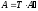 (1
(1 )
)
Координаты
вектора
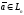 в новом базисе выражаются через
координаты вектора в старом базисе
в новом базисе выражаются через
координаты вектора в старом базисе

Формулы (18), (1 )
называют формулами преобразования
координат.
)
называют формулами преобразования
координат.
Евклидово пространство: основные понятия
Рассмотрим действительное линейное пространство L.
Определение
22. Будем
говорить, что в линейном пространстве
L
задано скалярное произведение, если
каждой паре векторов
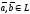 поставлено в соответствие действительное
число
поставлено в соответствие действительное
число
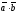 так, что выполняются следующие условия:
так, что выполняются следующие условия:
1)
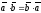 ;
;
2)
 ;
;
3)
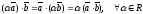 ;
;
4)
 ,
причем равенство нулю имеет место лишь
для нулевого вектора
,
причем равенство нулю имеет место лишь
для нулевого вектора
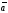 .
.
Определение 23. Линейное пространство L, в котором определено скалярное произведение, будем называть евклидовым пространством и обозначать E.
Если n-мерное линейное пространство — евклидово, то будем называть его евклидовым n-мерным пространством, а базис линейного пространства – базисом евклидова пространства.
Дадим определения длины вектора и угла между векторами в евклидовом пространстве E.
Определение
24. Длиной
вектора
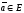 называется величина
называется величина
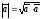 .
.
Углом
между векторами
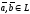 называется угол
называется угол
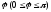 ,
косинус которого равен
,
косинус которого равен
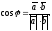
Определение
25. Два
вектора
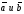 евклидова пространства E
называются
ортогональными,
если их скалярное произведение равно
нулю, т.е.
евклидова пространства E
называются
ортогональными,
если их скалярное произведение равно
нулю, т.е.
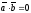 .
.
Пусть
в евклидовом пространстве
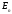 задан некоторый ортонормированный
базис
задан некоторый ортонормированный
базис
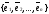 ,
т.е.
,
т.е.
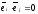 при
при
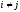 и
и
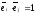 при
при
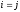 .
Если векторы
.
Если векторы
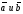 относительно данного базиса имеют
разложения
относительно данного базиса имеют
разложения
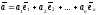 ,
,
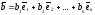 ,
то несложно показать, что скалярное
произведение
,
то несложно показать, что скалярное
произведение
 будет определяться формулой
будет определяться формулой
 .
(19)
.
(19)
Замечание.
Длину
вектора
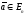 и
угол между векторами
и
угол между векторами
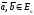 с учетом (4.19) можно вычислять по формулам
с учетом (4.19) можно вычислять по формулам
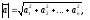 (20)
(20)
 (21)
(21)
