Понятие линейного пространства

Определение 16. Множество L элементов a, b, c, … произвольной природы называется линейным (векторным) пространством, если на этом множестве заданы две операции:

1) операция сложения (внутренняя операция), состоящая в том, что каждой паре элементов 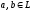ставится в соответствие по некоторому правилу или закону элемент , называемый суммой элементов 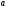и и обозначаемый ;

2) операция умножения элемента на действительное число (внешняя операция), состоящая в том, что каждому элементу 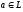и каждому числу 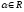ставится в соответствие по некоторому правилу или закону элемент , называемый произведением элемента на число и обозначаемый ,

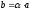причем эти операции удовлетворяют свойствам 1­–8, приведенным выше для векторов.

Элементы произвольного линейного пространства принято также называть векторами.

Замечание. В определении числа 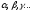— действительные, поэтому линейное пространство называется вещественным, или действительным линейным пространством. Если же 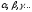— комплексные числа, то линейное пространство будет называться комплексным.

Примеры линейных пространств

1.. Такое линейное пространство называется нулевым, или тривиальным.

2. Множество свободных векторов, лежащих на одной прямой (плоскости или в обычном пространстве). Эти пространства мы будем обозначать , 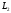и соответственно. Смысл нижних индексов выяснится позднее.

3. Множество прямоугольных матриц одного и того же размера.

4. Множество решений однородной системы линейных алгебраических урав­нений.

5. Множество, элементами которого являются упорядоченные наборы n действительных чисел: , если операции сложения элементов и умножение на действительное число 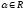определить следующим образом:

, .

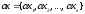6. Множество С [a, b] непрерывных на отрезке [a, b] функций f(t), если для этих функций естественным образом определены операции сложения и умножения на число.

Определение 17. Линейным подпространством линейного пространства называется непустое подмножество векторов из L, которые сами образуют линейное пространство относительно уже введенных в L операций сложения и умножения на число, т.е. такое подмножество, для которого выполнены 2 условия:

1.

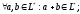
_2.

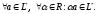
_{Тривиальными примерами линейных подпространств пространства L могут служить само пространство L а также множество, состоящее из одного нулевого элемента (нулевое подпространство).}

_{В пространстве L3 совокупность векторов, лежащих в какой-нибудь плоскости или какой-нибудь прямой, которые проходят через начало координат, будут образовывать линейные подпространства.}

Множество верхних треугольных (нижних треугольных) матриц является подпространствами линейного пространства, образованного множеством квадратных матриц одного и того же порядка.

Линейная зависимость и независимость системы n векторов

Пусть дана система n векторов 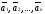и n действительных чисел .

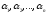Определение 18. Линейной комбинацией векторов 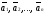будем называть вектор следующего вида

.

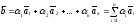Если 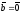, то получаем

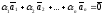. (15)

Определение 19. Система из n векторов называется линейно неза­висимой, если из равенства (15) следует, что все коэффициенты 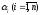равны нулю, т. е.

.

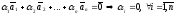Определение 20. Система из n вектор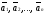ов называется линейно зависимой, если из равенства (13) следует, что хотя бы один из коэффициентов отличен от нуля, т.е.

.

Отметим следующие три свойства линейно зависимых систем векторов.

1. Если среди векторов 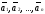хотя бы один вектор является нулевым, то такая система векторов линейно зависима.

Доказательство. Пусть, например, 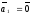. Тогда можно составить линейную комбинацию векторов

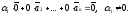
А это и означает, что векторы 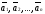линейно зависимы.▲

2. Система n () векторов линейно зависима тогда и только тогда, когда хотя бы один вектор этой системы можно представить в виде линейной комбинации остальных.

3. Если среди векторов 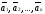имеется хотя бы одна подсистема линейно зависимых векторов, то вся система линейно зависима.