
- •Тема 1. Матричная алгебра План
- •Понятие матрицы. Виды матриц
- •Операции над матрицами и их свойства
- •I. Сложение матриц
- •II. Умножение матрицы на число
- •Свойства операций сложения и умножения на число:
- •III. Произведение матриц
- •Свойства операции умножения матриц:
- •IV. Транспонирование матриц
- •Свойства операции транспонирования:
- •Понятие определителя. Разложение определителя по элементам строки (столбца)
- •Свойства определителей
- •Базисный минор и ранг матрицы. Теорема о базисном миноре
- •Вычисление ранга матрицы методом окаймляющих миноров
- •Вычисление ранга матрицы с помощью элементарных преобразований
- •Обратная матрица и ее вычисление. Матричные уравнения
- •Свойства обратных матриц:
- •1) Если, то домножая обе части уравнения на слева, получим .
- •2) Если, то домножая обе части уравнения на справа, получим .
- •Использование алгебры матриц в экономике
- •Тема 2. Системы линейных уравнений План
- •Понятие системы линейных уравнений (слу)
- •Матричная форма записи слу
- •Условия совместности систем линейных уравнений. Теорема Кронекера–Капелли
- •Решение систем линейных уравнений методом обратной матрицы и по формулам Крамера
- •Метод Гаусса решения систем линейных уравнений
- •Однородные системы линейных уравнений
- •Фундаментальная система решений однородной системы линейных уравнений
- •Использование систем линейных уравнений в экономике
- •Модель Леонтьева многоотраслевой экономики
- •Экономико-математическая модель линейного обмена
- •Тема 3. Комплексные числа План
- •Понятие комплексного числа
- •Действия над комплексными числами
- •Тригонометрическая форма комплексного числа
- •Действия над комплексными числами в тригонометрической форме:
- •Тема 4. Элементы векторной алгебры План
- •Векторы на плоскости и в пространстве: основные понятия
- •Линейные операции над векторами
- •Свойства операций сложения векторов и умножения вектора на число
- •Координаты вектора на плоскости и в пространстве
- •Скалярное произведение векторов
- •Свойства скалярного произведения
- •Понятие линейного пространства
- •Примеры линейных пространств
- •Линейная зависимость и независимость системы n векторов
- •Примеры линейно зависимых и линейно независимых систем векторов
- •Базис. Координаты вектора в базисе
- •Матрица перехода к новому базису
- •Свойства матрицы перехода
- •Евклидово пространство: основные понятия
- •Выпуклые множества, свойства выпуклых множеств
- •Тема 5. Линейные отображения План
- •Понятие линейного оператора
- •Матрица линейного оператора
- •Действия над линейными операторами
- •Собственные векторы и собственные значения линейного оператора
- •Квадратичные формы
- •Критерий Сильвестра
Линейные операции над векторами
Под линейными операциями над векторами понимают операции сложения векторов и умножения вектора на число. Введем эти операции.
Определение
12. Пусть
даны два вектора
 .
Построим равные им векторы
.
Построим равные им векторы
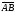 и
и
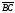 .
Вектор
.
Вектор
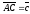 называется суммой
двух векторов
называется суммой
двух векторов
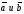 и обозначается
и обозначается
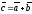 .
.
Таким образом, для любых точек А, В и С справедливо равенство
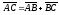 .
(1)
.
(1)
Указанное
в определении правило сложения векторов
называется правилом
треугольника.
Из него несложно получить еще одно
правило сложения векторов, известное
как правило
параллелограмма.
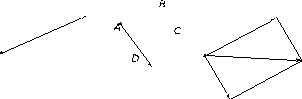
Оно состоит в следующем: если совместить
начала неколлинеарных векторов
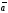 и
и
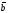 ,
отложить их от произвольной точки A
так, что
,
отложить их от произвольной точки A
так, что
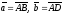 ,
и взять в качестве сторон параллелограмма
ABCD,
то вектор
,
и взять в качестве сторон параллелограмма
ABCD,
то вектор
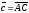 ,
лежащий на диагонали этого параллелограмма,
и есть сумма
,
лежащий на диагонали этого параллелограмма,
и есть сумма
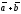 .
Таким образом,
.
Таким образом,
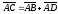 .
.
Замечание.
Правило
сложения можно распространить на любое
конечное число векторов. Для того чтобы
найти сумму векторов
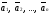 ,
нужно последовательно откладывать
данные векторы так, чтобы конец предыдущего
вектора совпадал с началом последующего.
В результате получится некоторая ломаная
линия, звеньями которой будут являться
данные векторы. Если эту ломаную замкнуть,
т.е. соединить начало первого вектора
с концом последнего, то получится вектор
,
нужно последовательно откладывать
данные векторы так, чтобы конец предыдущего
вектора совпадал с началом последующего.
В результате получится некоторая ломаная
линия, звеньями которой будут являться
данные векторы. Если эту ломаную замкнуть,
т.е. соединить начало первого вектора
с концом последнего, то получится вектор
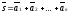 .
Сформулированное правило сложения n
векторов называют правилом
замыкания ломаной для многоугольника.
.
Сформулированное правило сложения n
векторов называют правилом
замыкания ломаной для многоугольника.
Определение
13.
Произведением
вектора
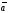 на число
на число
 (
(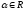 )
называется вектор
)
называется вектор
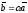 ,
удовлетворяющий следующим условиям:
,
удовлетворяющий следующим условиям:
1)
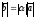 ,
где
,
где
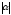 — модуль числа
— модуль числа
 .
.
2)
 ,
если
,
если
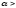 0;
0;
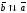 ,
если
,
если
 <
0.
<
0.
Замечание.
Если
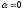 или
или
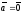 ,
то вектор
,
то вектор
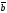 =
=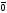 .
.
Замечание.
При умножении вектора
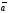 на число
на число
 получается вектор –
получается вектор –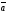 ,
противоположный вектору
,
противоположный вектору
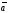 .
.
Свойства операций сложения векторов и умножения вектора на число
Для любых векторов
 и любых чисел
и любых чисел
 ,
,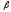 выполняется:
выполняется:
1)
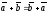 ;
;
2)
 ;
;
3)
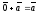 ;
;
4)
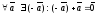 ;
;
5)
 ;
;
6)
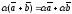 ;
;
7)
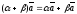 ;
;
8)
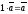 .
.
Следствие.
Разность
двух векторов
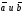 определяется как сумма векторов
определяется как сумма векторов
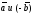 :
:
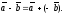
Координаты вектора на плоскости и в пространстве
Рассмотрим реальное пространство.
Напомним, что в трехмерном пространстве декартова прямоугольная система координат определяется заданием единицы для измерения длин и трех взаимно перпендикулярных осей, занумерованных в каком-либо порядке. Точка пересечения называется началом координат, а сами оси – координатными осями. Первая из координатных осей называется осью абсцисс, вторая – осью ординат, а третья – осью аппликат. Начало координат обозначается буквой О, а координатные оси обозначаются символами Ox, Oy, Oz соответственно. Декартова прямоугольная система кординат обозначается Oxyz.
Координатами произвольной точки А в заданной системе координат называются числа
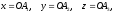
где
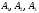 – проекции точки А на координатные оси,
а
– проекции точки А на координатные оси,
а
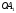 обозначает
величину отрезка
обозначает
величину отрезка
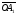 оси абсцисс,
оси абсцисс,
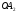 обозначает величину отрезка
обозначает величину отрезка
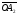 оси ординат,
оси ординат,
 обозначает величину отрезка
обозначает величину отрезка
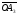 оси аппликат. Число x
называется абсциссой,
число y
называется ординатой,
а z
– аппликатой
точки
А.
Записывают: А(x,
y,
z).
оси аппликат. Число x
называется абсциссой,
число y
называется ординатой,
а z
– аппликатой
точки
А.
Записывают: А(x,
y,
z).
Напомним, что в
трехмерном пространстве – три базисных
вектора:
 – на оси абсцисс,
– на оси абсцисс,
 – на оси ординат,
– на оси ординат,
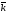 – на оси аппликат.
– на оси аппликат.
Пусть
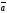 — произвольный вектор пространства.
Отложив вектор
— произвольный вектор пространства.
Отложив вектор
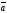 от начала координат, мы получим
упорядоченную тройку чисел (x,
y,
z)
– координаты конца А
отложенного вектора. Эти числа называются
координатами
вектора
от начала координат, мы получим
упорядоченную тройку чисел (x,
y,
z)
– координаты конца А
отложенного вектора. Эти числа называются
координатами
вектора
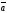 относительно
базиса
относительно
базиса
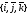 .
.

Так как
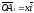 ,
,
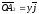 ,
,
 ,
а
,
а
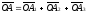 (см. рис.), то
(см. рис.), то
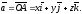 (2)
(2)
Замечание.
Вектор
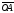 с началом в начале координат и концом
в точке А называется радиус-вектором
точки А. Таким образом, декартовыми
координатами вектора
с началом в начале координат и концом
в точке А называется радиус-вектором
точки А. Таким образом, декартовыми
координатами вектора
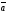 относительно данной системы координат
называются координаты конца равного
этому вектору радиус-вектора.
относительно данной системы координат
называются координаты конца равного
этому вектору радиус-вектора.
Из определения
координат вектора непосредственно
следует, что при сложении векторов их
координаты складываются, при вычитании
— вычитаются; при умножении вектора на
число — каждая координата умножается
на это число, т.е. если
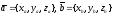 ,
то
,
то
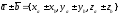 ;
;
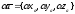 .
(3)
.
(3)
Признак
коллинеарности. Необходимым и
достаточным условием коллинеарности
двух векторов
 и
и
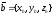
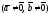 является пропорциональность их координат,
т.е.
является пропорциональность их координат,
т.е.
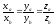 .
(4)
.
(4)
Признак
компланарности. Необходимым и
достаточным условием компланарности
трех ненулевых векторов
 ,
,
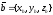 и
и
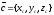 является равенство
является равенство

Рассмотрим некоторые задачи, которые пригодятся нам в дальнейшем.
Задача 1 (о нахождении координат вектора по координатам его начала и конца).
Рассмотрим две
точки А и В, причем
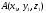 ,
,
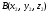 .
Найдем координаты вектора
.
Найдем координаты вектора
 (см. рис.).
(см. рис.).
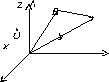
Решение. Из
рисунка видно, что
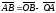 .
Так как
.
Так как
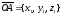 ,
,
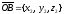 ,
то используя (4.3), получим:
,
то используя (4.3), получим:
 .
(6)
.
(6)
Таким образом, для того чтобы найти координаты вектора с известными координатами его начала и конца, нужно от координат конца вычесть координаты начала.
Задача
2 (о
делении отрезка в данном соотношении).
Рассмотрим отрезок
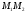 ,
причем
,
причем
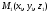 и
и
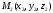 .
Пусть данный отрезок точкой M
делится в соотношении
.
Пусть данный отрезок точкой M
делится в соотношении
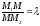 .
Найдем координаты точки М.
.
Найдем координаты точки М.
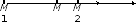
Решение. Из
рисунка видно, что справедливо векторное
равенство
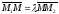 .
.
Предположим, что
точка M имеет координаты
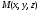 .
Находя по формуле (6)
координаты векторов
.
Находя по формуле (6)
координаты векторов
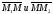 ,
перепишем равенство в виде:
,
перепишем равенство в виде:
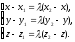
Выражая из первого равенства x, из второго – y, а из третьего – z, находим координаты точки М:
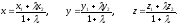 (7)
(7)
В случае если
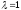 ,
т. е.
,
т. е.
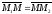 ,
получаем формулу координат середины
отрезка
,
получаем формулу координат середины
отрезка
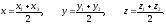 (7
(7 )
)
Замечание. На плоскости (в двумерном пространстве) можно так же задать прямоугольную систему координат Oxy. С помощью введенной системы координат любую точку или ее радиус-вектор можно представить парой чисел (x, y). Все соотношения, полученные нами ранее для координат векторов и точек трехмерного пространства, будут справедливы и на плоскости с той лишь разницей, что из них нужно всюду убрать третью координату z. Аналогичные рассуждения можно повторить и для произвольной прямой (одномерного пространства).
