- •Тема 1. Матричная алгебра План
- •Понятие матрицы. Виды матриц
- •Операции над матрицами и их свойства
- •I. Сложение матриц
- •II. Умножение матрицы на число
- •Свойства операций сложения и умножения на число:
- •III. Произведение матриц
- •Свойства операции умножения матриц:
- •IV. Транспонирование матриц
- •Свойства операции транспонирования:
- •Понятие определителя. Разложение определителя по элементам строки (столбца)
- •Свойства определителей
- •Базисный минор и ранг матрицы. Теорема о базисном миноре
- •Вычисление ранга матрицы методом окаймляющих миноров
- •Вычисление ранга матрицы с помощью элементарных преобразований
- •Обратная матрица и ее вычисление. Матричные уравнения
- •Свойства обратных матриц:
- •1) Если, то домножая обе части уравнения на слева, получим .
- •2) Если, то домножая обе части уравнения на справа, получим .
- •Использование алгебры матриц в экономике
- •Тема 2. Системы линейных уравнений План
- •Понятие системы линейных уравнений (слу)
- •Матричная форма записи слу
- •Условия совместности систем линейных уравнений. Теорема Кронекера–Капелли
- •Решение систем линейных уравнений методом обратной матрицы и по формулам Крамера
- •Метод Гаусса решения систем линейных уравнений
- •Однородные системы линейных уравнений
- •Фундаментальная система решений однородной системы линейных уравнений
- •Использование систем линейных уравнений в экономике
- •Модель Леонтьева многоотраслевой экономики
- •Экономико-математическая модель линейного обмена
- •Тема 3. Комплексные числа План
- •Понятие комплексного числа
- •Действия над комплексными числами
- •Тригонометрическая форма комплексного числа
- •Действия над комплексными числами в тригонометрической форме:
- •Тема 4. Элементы векторной алгебры План
- •Векторы на плоскости и в пространстве: основные понятия
- •Линейные операции над векторами
- •Свойства операций сложения векторов и умножения вектора на число
- •Координаты вектора на плоскости и в пространстве
- •Скалярное произведение векторов
- •Свойства скалярного произведения
- •Понятие линейного пространства
- •Примеры линейных пространств
- •Линейная зависимость и независимость системы n векторов
- •Примеры линейно зависимых и линейно независимых систем векторов
- •Базис. Координаты вектора в базисе
- •Матрица перехода к новому базису
- •Свойства матрицы перехода
- •Евклидово пространство: основные понятия
- •Выпуклые множества, свойства выпуклых множеств
- •Тема 5. Линейные отображения План
- •Понятие линейного оператора
- •Матрица линейного оператора
- •Действия над линейными операторами
- •Собственные векторы и собственные значения линейного оператора
- •Квадратичные формы
- •Критерий Сильвестра
Векторы на плоскости и в пространстве: основные понятия
Определение 1. Геометрическим вектором на плоскости или в трехмерном пространстве будем называть направленный отрезок, т.е. отрезок, у которого указано, какая его точка начальная, а какая конечная.
Вектор
с началом в точке А
и концом в точке В
будем обозначать
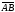 .
Точку А
вектора
.
Точку А
вектора
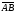 называют так же точкой
приложения вектора.
называют так же точкой
приложения вектора.
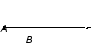
Векторы
также принято обозначать строчными
буквами
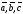 ,
… .
,
… .
Определение
2. Вектор
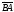 ,
т.е. вектор, начало которого совпадает
с точкой В,
а конец — с
точкой А,
называют противоположным
вектору
,
т.е. вектор, начало которого совпадает
с точкой В,
а конец — с
точкой А,
называют противоположным
вектору
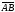 .
Если
.
Если
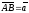 ,
то
,
то
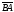 обозначают:
обозначают:
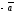 .
.
Замечание.
Для вектора
 противоположным является вектор
противоположным является вектор
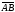 ,
т.е.
,
т.е.
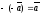 .
.
Определение
3. Вектор,
начало и конец которого совпадают,
называют нулевым
вектором
(нуль-вектором)
и обозначают
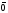 или пишут просто 0.
или пишут просто 0.
Определение
4. Длиной
(модулем,
или абсолютной
величиной)
вектора
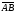 называется число (неотрицательное),
равное длине отрезка AB.
Обозначается
называется число (неотрицательное),
равное длине отрезка AB.
Обозначается
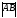 .
.
Длина нуль-вектора равна нулю.
Определение
5. Вектор,
длина которого равна единице, называется
единичным
вектором и
обозначается
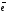 .
.
Определение
6. Единичный
вектор, направление которого совпадает
с направлением вектора
 ,
называется ортом
вектора и обозначается
,
называется ортом
вектора и обозначается
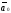 .
.
Определение 7. Два вектора называются коллинеарными, если они лежат на одной или на параллельных прямых, т. е. существует прямая, которой они параллельны.
Коллинеарные
векторы обозначаются
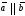 .
.
Теорема
1. Если
векторы
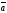 и
и
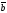 коллинеарные, то существует единственное
число
коллинеарные, то существует единственное
число
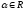 такое, что
такое, что
 .
.
Определение 8. Векторы называются компланарными, если они лежат в одной или параллельных плоскостях, т.е. существует плоскость, которой эти векторы параллельны.
Теорема
2. Если
векторы
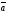 ,
,
 и
и
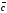 компланарные, то существуют единственные
числа
компланарные, то существуют единственные
числа
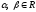 такие, что
такие, что
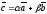 .
.
Теорема 3.
Пусть в трехмерном пространстве даны
три некомпланарных вектора
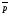 ,
,
 и
и
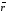 ,
тогда любой вектор
,
тогда любой вектор
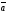 этого пространства можно разложить по
данным векторам, причем единственным
образом, т. е. существуют единственные
числа
этого пространства можно разложить по
данным векторам, причем единственным
образом, т. е. существуют единственные
числа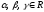 такие, что
такие, что
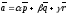 .
.
Определение
9. Два
коллинеарных вектора
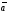 и
и
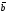 называются одинаково
направленными,
или сонаправленными,
если их концы лежат по одну сторону от
прямой, проведенной через их начала.
Если векторы
называются одинаково
направленными,
или сонаправленными,
если их концы лежат по одну сторону от
прямой, проведенной через их начала.
Если векторы
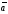 и
и
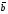 лежат на одной прямой, то они считаются
сонаправленными в случае, если лучи,
определяемые этими векторами,
содержатся один в другом. Обозначаются
лежат на одной прямой, то они считаются
сонаправленными в случае, если лучи,
определяемые этими векторами,
содержатся один в другом. Обозначаются
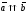 .
Коллинеарные векторы, не являющиеся
сонаправлеными, называются противоположно
направленными
и обозначаются
.
Коллинеарные векторы, не являющиеся
сонаправлеными, называются противоположно
направленными
и обозначаются
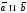 .
.
|
Сонаправленные векторы
( |
Противоположно направленные векторы
|
|
|
|
Определение
10. Два
вектора
 и
и
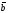 называются равными,
если они сонаправленные и имеют одинаковую
длину, т.е. выполнены следующие условия:
называются равными,
если они сонаправленные и имеют одинаковую
длину, т.е. выполнены следующие условия:
1.
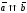 ;
;
2.
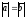
Определение 11. Пусть дан направленный отрезок (геометрический вектор). Множество всех направленных отрезков, равных данному, называется свободным вектором.
Другими словами, свободный вектор это геометрический вектор, который можно переносить параллельно самому себе. В дальнейшем мы будем рассматривать свободные векторы.

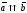 ,
,
 )
)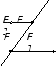 (
(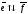 ,
,
 )
)