
- •Тема 1. Матричная алгебра План
- •Понятие матрицы. Виды матриц
- •Операции над матрицами и их свойства
- •I. Сложение матриц
- •II. Умножение матрицы на число
- •Свойства операций сложения и умножения на число:
- •III. Произведение матриц
- •Свойства операции умножения матриц:
- •IV. Транспонирование матриц
- •Свойства операции транспонирования:
- •Понятие определителя. Разложение определителя по элементам строки (столбца)
- •Свойства определителей
- •Базисный минор и ранг матрицы. Теорема о базисном миноре
- •Вычисление ранга матрицы методом окаймляющих миноров
- •Вычисление ранга матрицы с помощью элементарных преобразований
- •Обратная матрица и ее вычисление. Матричные уравнения
- •Свойства обратных матриц:
- •1) Если, то домножая обе части уравнения на слева, получим .
- •2) Если, то домножая обе части уравнения на справа, получим .
- •Использование алгебры матриц в экономике
- •Тема 2. Системы линейных уравнений План
- •Понятие системы линейных уравнений (слу)
- •Матричная форма записи слу
- •Условия совместности систем линейных уравнений. Теорема Кронекера–Капелли
- •Решение систем линейных уравнений методом обратной матрицы и по формулам Крамера
- •Метод Гаусса решения систем линейных уравнений
- •Однородные системы линейных уравнений
- •Фундаментальная система решений однородной системы линейных уравнений
- •Использование систем линейных уравнений в экономике
- •Модель Леонтьева многоотраслевой экономики
- •Экономико-математическая модель линейного обмена
- •Тема 3. Комплексные числа План
- •Понятие комплексного числа
- •Действия над комплексными числами
- •Тригонометрическая форма комплексного числа
- •Действия над комплексными числами в тригонометрической форме:
- •Тема 4. Элементы векторной алгебры План
- •Векторы на плоскости и в пространстве: основные понятия
- •Линейные операции над векторами
- •Свойства операций сложения векторов и умножения вектора на число
- •Координаты вектора на плоскости и в пространстве
- •Скалярное произведение векторов
- •Свойства скалярного произведения
- •Понятие линейного пространства
- •Примеры линейных пространств
- •Линейная зависимость и независимость системы n векторов
- •Примеры линейно зависимых и линейно независимых систем векторов
- •Базис. Координаты вектора в базисе
- •Матрица перехода к новому базису
- •Свойства матрицы перехода
- •Евклидово пространство: основные понятия
- •Выпуклые множества, свойства выпуклых множеств
- •Тема 5. Линейные отображения План
- •Понятие линейного оператора
- •Матрица линейного оператора
- •Действия над линейными операторами
- •Собственные векторы и собственные значения линейного оператора
- •Квадратичные формы
- •Критерий Сильвестра
Тема 3. Комплексные числа План
Понятие комплексного числа. Операции над комплексными числами. Модуль и аргумент комплексного числа. Геометрическая интерпретация комплексных чисел. Тригонометрическая форма комплексного числа. Операции над комплексными числами в тригонометрической форме.
Понятие комплексного числа
Определение
1.
Число вида x+yi,
где x
и у
– действительные числа, а i
– число, квадрат которого равен минус
единице (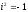 ),
называется комплексным
и обозначается z,
т.е.
),
называется комплексным
и обозначается z,
т.е.
z=x+yi. (1)
Число x называется действительной частью комплексного числа z и обозначается Re z , а число у – мнимой часть комплексного числа z и обозначается Im z. Число z= i называется мнимой единицей. Множество всех комплексных чисел обозначается буквой С.
Выражение (1) называется алгебраической формой комплексного числа z.
Замечание. Действительные числа являются частным случаем комплексных чисел. Именно, любое действительное число x можно рассматривать как комплексное число x+0i.
Определение 2. Два комплексных числа z1=x1+y1i и z2=x2+y2i называются равными, если x1= x2 и y1= y2.
Замечание. Неравные комплексные числа в общем случае несравнимы между собой.
Определение
3.
Комплексные числа
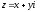 и
и
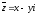 называются
сопряженными
(друг другу).
называются
сопряженными
(друг другу).
Действия над комплексными числами
Правила сложения, вычитания, умножения и деления комплексных чисел z1=x1+y1i и z2=x2+y2i:
1.
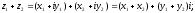
2.
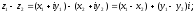
3.

4.

Тригонометрическая форма комплексного числа
Из
(1) следует, что между комплексными
числами и точками координатной плоскости
существует взаимно-однозначное
соответствие:
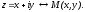
Поэтому
любое комплексное число z=x+iy
можно изобразить точкой М(x,
y)
координатной плоскости или ее
радиус-вектором
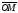 .
Длина этого вектора
.
Длина этого вектора
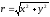 называется
модулем
комплексного числа
z
и обозначается
называется
модулем
комплексного числа
z
и обозначается
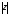 ,
т.е.
,
т.е.
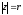 ,
а угол
,
а угол
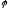 между осью Ох и вектором
между осью Ох и вектором
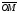 ,
измеряемый против часовой стрелки,
называется аргументом
комплексного числа
z
и обозначается
аrg
z,
т.е.
,
измеряемый против часовой стрелки,
называется аргументом
комплексного числа
z
и обозначается
аrg
z,
т.е.
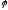 =
аrg
z.
Будем полагать, что
=
аrg
z.
Будем полагать, что
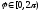 .
.
Из прямоугольного треугольника ОАМ находим:
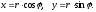 (2)
(2)
Подставляя (2) в (1), получим тригонометрическую форму комплексного числа:
 (3)
(3)
где
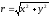 ,
а
,
а
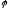 –
решение системы
–
решение системы
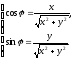
Действия над комплексными числами в тригонометрической форме:
1.
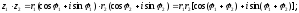
2.
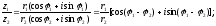
3. Формула Муавра:
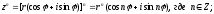
4.

Тема 4. Элементы векторной алгебры План
Векторы на плоскости и в пространстве: основные понятия, линейные операции над векторами, координаты вектора, скалярное произведение векторов. Понятия линейного пространства и подпространства, примеры. Линейная зависимость и независимость системы n векторов. Свойства линейной зависимости векторов. Примеры линейно зависимых и линейно независимых систем векторов. Базис, разложение вектора по базису. Матрица перехода к новому базису и ее свойства. Евклидово пространство. Выпуклые множества. Свойства выпуклых множеств. Решение системы неравенств.
