85

Тема 1. Матричная алгебра План

Понятие матрицы, виды матриц. Операции над матрицами и их свойства. Понятие определителя. Разложение определителя по элементам строки (столбца). Свойства определителей. Ранг матрицы. Обратная матрица. Матричные уравнения. Использование алгебры матриц в экономике.

Понятие матрицы. Виды матриц

Определение 1. Матрицей размера mn (m,nN) называется совокупность mn чисел, заданных в виде прямоугольной таблицы, состоящей из m строк и n столбцов

(1)

Если число строк в таблице не совпадает с числом столбцов, т.е. 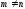, то матрица называется прямоугольной. Матрица, у которой число строк равно числу столбцов (m=n), называется квадратной порядка n.

Числа из таблицы (1) будем называть элементами матрицы. Элемент, стоящий на пересечении i-й строки и j-го столбца матрицы A, обозначается 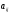. Условимся, что все элементы рассматриваемых нами матриц – действительные числа; будем называть такие матрицы действительными.

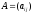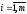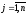Матрицы обозначаются прописными латинскими буквами, а их элементы соответствующими строчными. Для обозначения матрицы (1) употребляется также запись: , где ;, или A, когда хотят указать размер матрицы. Для квадратных матриц n-го порядка вместо A будем писать .

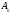Определение 2. Две матрицы 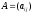и 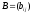называются равными, если они одинаковых размеров, и их соответствующие элементы равны, т. е. ; .

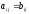
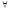
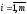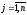Определение 3. Диагональ квадратной матрицы, идущая от левого верхнего к правому нижнему углу (составленная из элементов 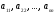) называется главной, а диагональ, идущая от верхнего правого к нижнему левому углу (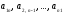) – побочной.

Определение 4. Квадратную матрицу 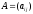; 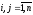, у которой все элементы, расположенные на главной диагонали равны единице, а остальные –нулю, будем называть единичной и обозначать E. Она имеет вид

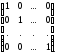(2)

Определение 5. Матрица O произвольных размеров, у которой все элементы равны нулю, называется нулевой.

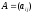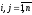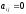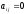Определение 6. Квадратная матрица ; называется треугольной, если все элементы матрицы, расположенные под главной диагональю (над главной диагональю) равны нулю, т. е. при i >j ( при i < j),

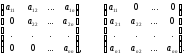(3)

Первую из этих матриц называют верхней треугольной, а вторую – нижней треугольной.

Определение 7. Матрица произвольного размера

(4)

называется трапециевидной.

Определение 8. Прямоугольные матрицы размера m1 (1n) называются столбцевыми (строчными) матрицами.

Часто удобно рассматривать матрицу как совокупность строк или столбцов. Например, матрицу (1) можно представить как строчную матрицу 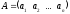размера 1n, где каждый элемент 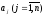– столбец высоты m:

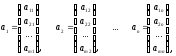(5)

или в виде столбцевой матрицы 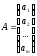размера m1, где каждый элемент 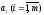– строка длиной n:

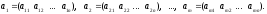(6)

Операции над матрицами и их свойства

I. Сложение матриц

Определение 9. Суммой двух матриц 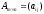и 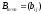называется матрица 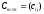такая, что

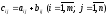, (7)

т.е. каждый элемент матрицы С равен сумме соответствующих элементов матриц А и В.

Сумма матриц А и В обозначается A+B.