Элементы квантовой статистики

 

Лекция n 11

Электронный газ при Т > 0. Распределение Ферми-Дирака. Анализ функции f(Е)

 

§ 1. Электронный газ при T > 0. Распределение Ферми-Дирака

Рис. 11.1

На приведенных выше рисунках 11.1 изображена одномерная потенциальная яма, заполненная электронным газом; на рис. а) при T = 0, на рис. б)  при T > 0. Слева от потенциальной ямы изображены графики зависимости среднего по времени числа электронов в одном квантовом состоянии - <n(E)> - от энергии электронов E. Энергия E отложена по вертикальной оси, проходящей вдоль левой границы ямы, сама функция <n(E)> отложена по горизонтальной оси, направленной влево.

При T = 0K электроны занимают все доступные им состояния с наинизшей энергией. В соответствии с принципом Паули  в каждом квантовом состоянии может находиться не более одного фермиона, поэтому все нижние квантовые состояния до энергии E_F(0)  заняты. Таким образом, график функции <n(E)> представляет из себя ступеньку:

<n(E)> = 1 при E < E_F(0)  и  <n(E)> = 0 при E > E_F(0).

При нагревании металла часть электронов, энергия которых была близка к энергии Ферми, переходят в состояния с большей энергией, частично освобождая квантовые состояния с энергией E < E_F(0): ступенька графика <n(E)> размывается.

Аналитическую зависимость среднего числа ферминов в одном квантовом состоянии от их энергии и температуры получили итальянский физик Э. Ферми и английский физик П. Дирак.

Она имеет следующий вид:

и называется распределением Ферми-Дирака. Параметр E_F, входящий в распределение Ферми-Дирака, называется уровнем Ферми. В статистической физике этот параметр называется химическим потенциалом, его обозначают буквой µ, таким образом µ ≡ E_F.

Среднее число электронов в одном квантовом состоянии <n(E)> изменяется от нуля до единицы, в этих же пределах изменяется вероятность f(E_i) заполнения данных квантовых состояний.

Таким образом

С учетом того, что E_F ≡µ, функцию распределения Ферми-Дирака можно записать в таком виде:

Значение уровня Ферми E_F (или химического потенциала µ) определяют из условия нормировки  функции f(E_i): полное число электронов, находящихся во всех квантовых состояниях должно быть равно числу N свободных электронов в рассматриваемом объеме V.

Среднее число электронов в одном квантовом состоянии дается функцией Ферми-Дирака f(E_i) (11.1а). Так как расстояния между соседними уровнями при макроскопических объемах образца малы, то можно считать, что энергия меняется непрерывным образом, т.е. f(E_i) →  f(E).

Число квантовых состояний, приходящихся на интервал энергий dE получим, умножив плотность состояний g(E) (10.9) на dE. Число электронов dN, имеющих энергию в интервале от E до E+dE, получим, умножив f(E) на g(E)dE, т.е.

Наконец, проинтегрировав dN, получим N - полное число электронов в образце:

Это и есть условие нормировки функции распределения Ферми-Дирака.

Значение E_F (или химический потенциал µ) можно найти, подставив в условие нормировки (11.2) f(E) из (11.1а) и g(E) из (10.9). Однако аналитическое выражение для получающегося интеграла отсутствует. При не очень высоких температурах, таких, что kT << E_F, для уровня Ферми получается приближенное выражение:

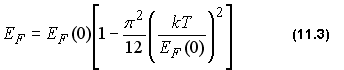
Здесь E_F(0) определяется формулой (10.9).