11.5.1. Оценка точности интегрирования по формуле левых прямоугольников

Представим точное выражение для интеграла на частичном отрезке [x_i-1, x_i] при помощи погрешности R_i в виде:

, (11.33)

Разлагая подынтегральную функцию f(x) в окрестности левой точки x_i-1 на частичном отрезке [x_i-1, x_i] в ряд Тейлора с точностью до слагаемых второго порядка малости по разности (x -x_i-1), получим:

(11.34)

Подставим данное разложение в частичный интеграл и выполним интегрирование каждого из слагаемых по x на отрезке [x_i-1, x_i]:

После подстановки полученного приближенного значения интеграла в формулу (11.33), получим следующую оценку погрешности интегрирования R_i на частичном отрезке [x_i-1, x_i]:

Рассматривая полный отрезок интегрирования [a,b], после суммирования частичных погрешностей получим для него оценку полной погрешности R:

Заменяя по методу левых прямоугольников выражение в квадратных скобках интегралом на отрезке интегрирования [a,b] от первой производной, получим для полной погрешности R оценку вида:

(11.35)

11.5.2. Оценка точности интегрирования по формуле средних прямоугольников

Аналогично представим точное выражение для интеграла на частичном отрезке [x_i-1, x_i] при помощи частичной погрешности R_i в виде:

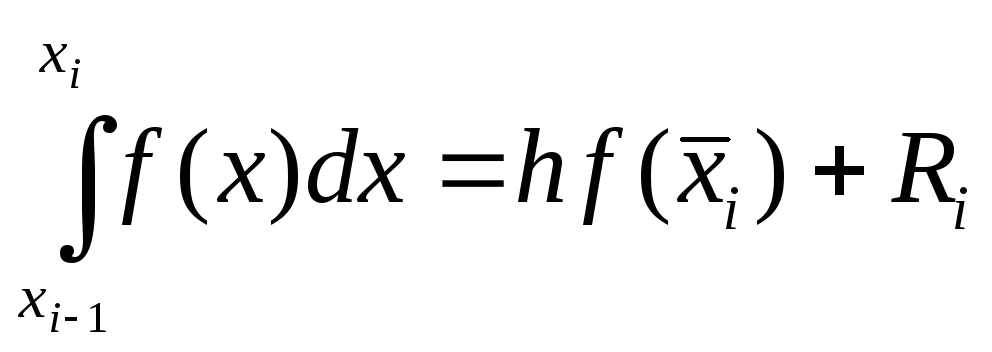, (11.36)

где x_i = 0,5(x_i-1+ x_i) - средняя точка отрезка [x_i-1, x_i].

Разлагаем подынтегральную функцию f(x) в окрестности средней точки x_i на частичном отрезке [x_i-1, x_i] в ряд Тейлора с точностью до слагаемых третьего порядка малости по разности (x -x_i):

(11.37)

Подставим данное разложение в частичный интеграл и выполним интегрирование каждого из слагаемых по x на отрезке [x_i-1, x_i]:

Аналогично переходя к полному отрезку интегрирования [a,b], получим для него оценку полной погрешности:

Заменив по методу средних прямоугольников выражение в квадратных скобках интегралом на полном отрезке [a,b] по методу средних прямоугольников от второй производной, получим оценку полной погрешности вида:

(11.38)

Аналогично можно получить априорные оценки погрешностей других методов. При этом получаются следующие зависимости:

1. метод трапеций: (11.39)

2. метод Симпсона: . (11.40)

Приведенные выводы оценок величин абсолютных погрешностей методов численного интегрирования Ньютона-Котеса имеют общий алгоритм, по которому:

1) вначале подынтегральная функция f(x) разлагается на каждом частичном отрезке [x_i-1, x_i] в окрестности точки интегрирования с необходимой точностью в ряд Тейлора,

2) затем данное разложение подставляют в частичный интеграл и в нем выполняется интегрирование каждого из слагаемых по x на отрезке [x_i-1, x_i],

3) оценка для полной погрешности получается путем суммирования всех частных погрешностей и перехода в полученной сумме к интегралу по производной соответствующего порядка.

Полученные формулы (11.35), (11.38), (11.39), (11.40) задают теоретическую априорную оценку погрешности вычисления интеграла рассмотренными выше методами. Для их применения не требуется расчета интеграла от функции. Степень шага h, входящая в формулу для общей погрешности интегрирования R, называют порядком метода интегрирования. Из приведенных формул следует, что методы левых и правых прямоугольников имеют первый порядок, методы средних прямоугольников и трапеций - второй, метод Симпсона имеет четвертый порядок.

Так как у метода трапеций константа при h² в два раза больше, чем у метода средних прямоугольников, то при аналитическом задании функции из методов второго порядка предпочтительнее применять метод средних прямоугольников из-за его меньшей погрешности. Метод Симпсона имеет четвертый порядок точности с очень малым численным коэффициентом. Поэтому формула Симпсона позволяет получить очень высокую точность, если четвертая производная подынтегральной функции не слишком велика. В противном случае, методы второго порядка точности могут дать большую точность, чем метод Симпсона.

Вопросы для проверки знаний.

1. Какова общая структура квадратурных формулы, получаемых по методу Ньютона-Котеса для приближенного вычисления определенных интегралов ?

2. Какой общий алгоритм используется для получения оценок величин абсолютных погрешностей методов численного интегрирования Ньютона-Котеса ?

3. Какой вид аппроксимации точного значения подынтегральной функции используется при оценке погрешности интегрирования на каждом частичном отрезке ?

4. Почему в общем случае метод средних квадратов точнее метода трапеций ?

5. В каких случаях метод Симпсона может дать худшие результаты по сравнению с методами второго порядка ?