11.2. Численное интегрирование. Классификация методов
В простейшем случае задачей интегрирования является вычисление для непрерывной функции f(x) на отрезке [a,b] определенного интеграла вида
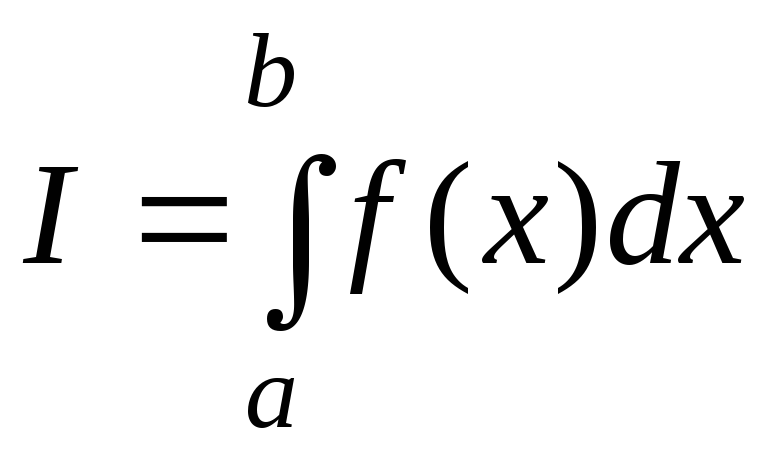(11.14)
Геометрический смысл определенного интеграла - площадь под кривой f(x) на отрезке [a,b]. Функцию f(x) называют подынтегральной.
Если подынтегральная функция f(x) задана в аналитическом виде и неопределенный интеграл от f(x) можно выразить через элементарные функции в виде первообразной F(x), то определенный интеграл (11.14) можно вычислить непосредственно с помощью F(x) по формуле Ньютона-Лейбница. Она состоит в том, что определенный интеграл равен приращению первообразной на отрезке интегрирования:
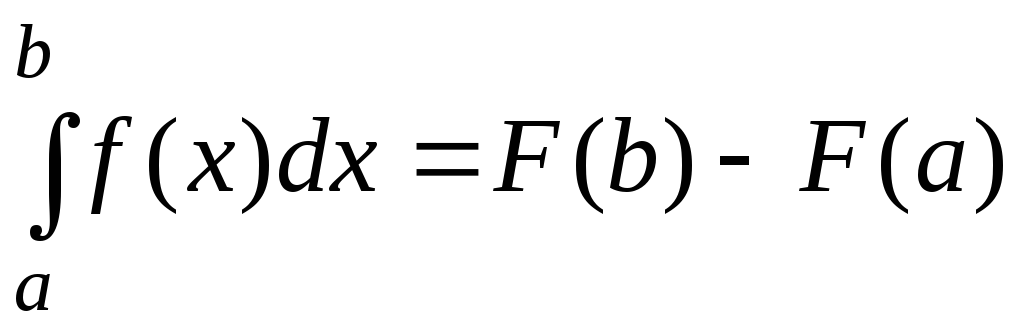. (11.15)
Однако на практике расчет определенных интегралов по формуле Ньютона-Лейбница (11.15) зачастую невозможен по следующим основным причинам:
1) для заданной подынтегральной функции f(x) невозможно аналитически выразить ее первообразную F(x) через элементарные функции;
2) для подынтегральной функции f(x) не существует аналитического выражения, например, она задана таблично.
В этих случаях используют приближенные, численные методы расчета определенных интегралов.
11.2.1. Классификация методов численного интегрирования
Основная идея численного интегрирования заключается в том, что подынтегральную функцию f(x) аппроксимируют на отрезке [a,b] другой функцией (x), для которой легко определяется первообразная:
f(x) (x), x [a,b].
При этом:
(11.16)
где R – погрешность вычисления интеграла.
Поскольку не существует универсальных методов аппроксимации, обеспечивающих интегральную близость функций f(x) и (x), то для повышения точности операции интегрирования применяют кусочную аппроксимацию f(x), при которой весь отрезок интегрирования [a,b] разбивают на n частичных отрезков [xi, xi+1] (i = 0,1,...,n-1, a = x0 < x1 <...< b = xn) и на каждом частичном отрезке [xi, xi+1] f(x) заменяют аппроксимирующей функцией i(x). В этом случае приближенное значение определенного интеграла равно сумме частичных интегралов от функций i(x), взятых на соответствующих частичных отрезках [xi-1, xi] (i = 1,2,...,n):
.
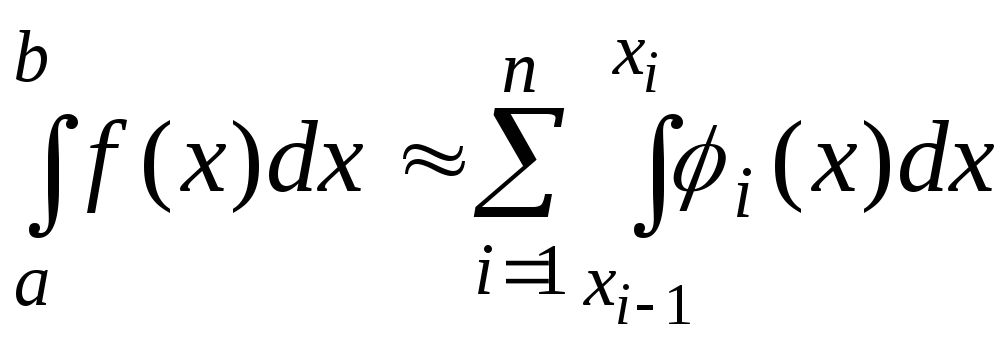(11.17)
Методы численного интегрирования различаются по:
1) способам аппроксимации подынтегральной функции f(x) функциями {i(x)} и
2) методам выбора узловых точек аппроксимации {xi} на отрезке интегрирования [a,b].
1. Методы Ньютона-Котеса. Используется полиномиальная аппроксимация подынтегральной функции f(x) – интерполяция ее значений полиномами, проходящими через узловые точки f(x). Методы этого класса отличаются друг от друга степенью используемого полинома, от которого зависит количество интерполяционных узлов. Узлы интегрирования выбираются на равномерной сетке с постоянным шагом h = (b-a)/n, который называют шагом интегрирования. Алгоритмы этих методов просты и легко поддаются программной реализации.
2. Сплайновые методы основаны на аппроксимации подынтегральной функции f(x) сплайнами. Методы различаются по типу выбранных сплайнов. Такие методы имеет смысл использовать в задачах, где алгоритмы сплайновой аппроксимации применяются для обработки данных, т.е. к моменту расчета интеграла уже имеется достаточно точная аппроксимация подынтегральной функции f(x) сплайнами.
3. Методы наивысшей алгебраической точности (методы Гаусса) используют неравноотстоящие узлы, расположенные так, чтобы обеспечить минимальную погрешность интегрирования для наиболее сложных (например, быстро осциллирующих) функций при заданном количестве узлов. Методы различаются способом выбора узлов и широко используются для интегрирования, в том числе они применимы и для несобственных интегралов. Однако, по сравнению с методами Ньютона-Котеса, методы Гаусса более громоздки и требуют несколько больших объемов памяти.
4. Методы Монте-Карло используют узлы, расположение которых выбирается с помощью датчика случайных чисел, результат в итоге носит вероятностный характер. Методы оказываются особенно эффективны при вычислении кратных интегралов.
Независимо от выбранного метода в процессе численного интегрирования необходимо вычислить приближенное значение интеграла и оценить погрешность интегрирования R.
Погрешность R, возникающая при численном интегрировании, также, как и при численном дифференцировании, имеет два основных источника. Первым источником погрешности является приближенная замена подынтегральной функции аппроксимирующей функцией – погрешность аппроксимации. Как будет показано ниже, погрешность аппроксимации уменьшается с увеличением количества отрезков разбиения интервала интегрирования n за счет более точной аппроксимации подынтегральной функции. Другой источник погрешности – неточности в вычислении подынтегральной функции в узловых точках и ошибки округления. Эта погрешность возрастает с ростом n и, начиная с некоторого значения nпред, начинает преобладать над погрешностью аппроксимации. Поэтому оптимальное значение n необходимо выбирать с учетом всех источников погрешностей интегрирования.
Все методы имеют свои достоинства и недостатки. Их применяют в зависимости от особенностей решаемой задачи численного интегрирования.
Вопросы для проверки знаний.
1. Как можно найти определенный интеграл в случае существования у подынтегральной функции аналитической первообразной ?
2. В каких случаях применяют численное дифференцирование ?
3. В чем заключается основная идея численного интегрирования ?
4. Какой универсальный метод применяют для повышения точности операции интегрирования ?
5. По каким двум основным признакам различаются методы численного интегрирования ?
6. В чем заключаются методы Ньютона-Котеса ?
7. Какой способ аппроксимации подынтегральной функции используется в сплайновых методах численного интегрирования ?
8. В чем заключаются методы наивысшей алгебраической точности (методы Гаусса) ?
9. Какой способ выбора узлов используют в методах Монте-Карло ?
10. Из каких соображений следует выбирать оптимальное число узлов при численном интегрировании ?