11.6. Вычисление интеграла с заданной точностью
Используя приведенные выше оценки погрешности методов численного интегрирования Ньютона-Котеса теоретически можно априори (до проведения расчета) определить шаг интегрирования h, при котором абсолютная погрешность вычисленного результата гарантированно не превысит допустимое значение . Однако использование таких оценок в общем случае сводит задачу интегрирования функций к еще более сложной задаче интегрирования их производных. Поэтому на практике наряду с априорными используют апостериорные методы оценки погрешности операции численного интегрирования, основанные на анализе результатов предварительных расчетов.
11.6.1. Интегрирование с постоянным шагом. Метод Рунге апостериорной оценки погрешности численного интегрирования
Обозначим точное значение искомого интеграла от функции f(x) на отрезке [a, b] через I. Допустим, численный расчет интеграла выполняется по приближенному методу М, имеющим порядок р, с постоянным шагом h и получено расчетное значение, которое обозначим через I(h). Если уменьшить шаг интегрирования в 2 раза и определить для шага h/2 тем же методом приближенное значение интеграла I(h/2), то из априорной оценки погрешности для метода интегрирования М следует, что в первом и втором случаях верны следующие соотношения:
I - I(h) C(h)р,
I - I(h/2) C(h/2)р,
где C=C(f(x),a,b,M) - величина, зависящая от интеграла некоторой производной функции f(x) на отрезке [a, b].
Определим из данных оценок зависимость неизвестной погрешности I - I(h/2) от полученных численных значений интеграла I(h) и I(h/2). Вычитая из первой оценки вторую, получим:
I(h/2) - I(h) Ch р (2р -1)/2р.
Отсюда вытекает:
I - I(h/2) Ch/2р = (I(h/2) - I(h))/(2р -1).
Переходя к абсолютным величинам, получим приближенную оценку абсолютной погрешности для метода интегрирования порядка р, которую называют правилом Рунге:
(I(h/2)) = I - I(h/2) I(h/2) - I(h) /(2р -1). (11.41)
Правило Рунге для рассмотренных методов в зависимости от их порядка р дает следующие оценки.
1. Методы левых и правых прямоугольников (р = 1):
I - I(h/2) I(h/2) - I(h). (11.41а)
2. Методы средних прямоугольников и трапеций (р = 2):
I - I(h/2) I(h/2) - I(h)/3. (11.41б)
3. Метод Симпсона (р = 4):
I - I(h/2) I(h/2) - I(h)/15. (11.41б)
Из правила Рунге вытекает, что для метода интегрирования порядка р требуемая точность интегрирования будет получена уже у интеграла I(h/2), если для последовательно найденных значений I(h/2) и I(h) выполняется соотношение:
I(h/2) - I(h) (2р -1).
Если данное условие не выполнено, то требуется продолжить уменьшение шага, найти интеграл I(h/4) и применить правило Рунге к значениям I(h/4) и I(h/2) и т.д.
При расчете нового значения интеграла I(h/2) при двойном уменьшении шага для сокращения расчетов необходимо использовать уже известное значение I(h). Например, в методах левых и правых прямоугольников, трапеций:
I(h/2) = I(h)/2 + (h/2)( f(xн1)+...+ f(x нк)),
где xн1,..., x нк - новые узловые точки в I(h/2), которые добавляются к прежним в I(h).
Пример 1. Рассчитать с использованием правила Рунге интеграл функции f(x)=sin(x) на отрезке [0, /2] с точностью = 0,02 по методу трапеций. Погрешность полученного значения проверить по точному решению.
Решение. Расчеты будем выполнять с точностью до третьего знака после запятой. Метод трапеций имеет второй порядок (р = 2), для численного расчета интеграла по нему используем формулу (11.28):
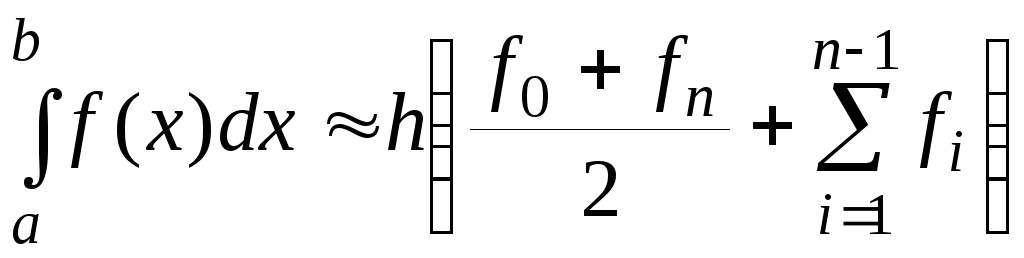
1.Вначале принимаем начальный шаг интегрирования равным всему отрезку:
h = b-a = /2. Найдем численное значение интеграла:
I(h) = (/2)((sin(0)+ sin(/2))/2)= (/2)((0+1)/2)= /4 0,785.
2. Уменьшим шаг интегрирования в 2 раза: h/2 = /4. Численное значение интеграла:
I(h/2) = I(h)/2 + (h/2)sin(/4) = 0,785/2 + (/4)(0,707) 0,393 +0,555 = 0,948.
Оценим абсолютную погрешность последнего значения по правилу Рунге (11.41б) и сравним ее с заданной точностью :
I - I(h/2) I(h/2) - I(h)/3 0,948 - 0,785/3 0,054 > = 0,02.
Проверка показывает недостаточную точность расчета интеграла, следовательно, шаг необходимо уменьшить.
3. Уменьшим шаг интегрирования в 2 раза: h/4 = /8. Численное значение интеграла:
I(h/4) = I(h 2)/2 + (/8)(sin(/8)+ sin(3/8)) = 0,948/2 + (/8)(0,383+0,984) 0,474 + 0,513 = 0,987.
Оценим погрешность последнего значения по правилу Рунге и сравним ее с :
I - I(h/4) I(h/4) - I(h/2)/3 0,987 - 0,948/3 0,013 < = 0,02.
Проверка выполнена, принимаем в качестве значения искомого интеграла значение I(h/4) =0,987.
Первообразная функции f(x): F(x) = -cosx. Точное значение рассмотренного определенного интеграла на отрезке [0;/2] равно: I = (-cos(/2)-(-cos(0)) 1. Точное (до округления величин) значение абсолютной погрешности расчета интеграла равно: I - I(h/4) = 0,013. Оно не превышает заданной точности = 0,02.