1. Составление т-обратной схемы

Это эквивалентная схема, в которой получаются те же уравнения, что и в схеме с магнитной связью (между L₁ и L₂). Такая замена возможна только если индуктивности соединены проводником. Нижний конец буквы Т направляется в место соединения магнитно связанных индуктивностей Когда есть магнитная связь, нельзя применять МУН. Поэтому делают развязку магнитных связей.

Уравнения по МКТ должны быть в схемах одинаковыми. Знак без скобок выбирается при соединение вместе одинаковых (одноименных) зажимов L₁ и L₂ и в скобках при не одноименных..

2. Развязка с использованием зависимых источников

§5. Автотрансформатор

Автотрансформатор – трансформатор, у которого вторичная обмотка является частью первичной обмотки, с целью экономии провода. Здесь вместе соединены разноименные зажимы.

§6. Общие методы расчета цепей с взаимными индуктивными элементами

1. Используют метод токов ветвей

2. Используют метод контурных токов, хотя иногда возникают трудности, с учетом взаимного влияния по магнитному полю

3. Метод узловых напряжений применять нельзя, можно только после развязки индуктивных связей

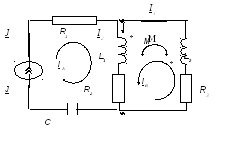
Число уравнений . Выбираем направление комплексных контурных токов и как показано. Составим уравнение для определения неизвестного контурного тока . Схема со взаимной индуктивностью, поэтому необходимо учитывать влияние контурных токов и , протекающих через индуктивные элементы по магнитному полю. Ветвь с током является общей для контурных токов и . В ветви с током контурный ток создает напряжение взаимоиндукции , которое следует взять со знаком “ + ”, т.к. контурные токи и направлены одинаково относительно одноименных зажимов, помеченных «звездочками». В свою очередь, контурный ток создает одинаковые напряжения взаимной индукции в ветвях с токами и соответственно. При этом данные напряжения следует взять со знаком “ + ”, т.к. контурный ток одинаково ориентирован относительно одноименных зажимов. Таким образом, уравнение будет иметь следующий вид:

Через контурный ток определяем неизвестные токи ветвей и Рассчитаем напряжение на индуктивности L₁ согласно второму закону Кирхгофа. Оно будет определятся напряжением самоиндукции и напряжением взаимоиндукции , взятого со знаком “–”, поскольку направление и направление тока ориентированы относительно одноименных зажимов различно. Следовательно:

6. Резонансные явления и колебательные контуры в электрических цепях

§1. Понятие о резонансе в эц

Под резонансом понимают такой режим работы электрической цепи, содержащей RL- и RC-элементы, когда угол сдвига фаз между напряжением и током на какой-то частоте равен 0. Это так называемый фазовый резонанс. Есть амплитудный резонанс, когда достигается максимальная амплитуда колебаний напряжения или тока. Он не является основным для ТЭЦ, основной – фазовый. Резонансная частота определяется по нулевому фазовому сдвигу.

Различают резонанс напряжений, L и C соединены последовательно (индуктивное напряжение компенсируется емкостным) и резонанс токов, L и C – параллельно (индуктивный ток компенсируется емкостным);

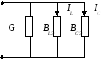
X=0 = X_LЭ - X_CЭ – резонанс напряжений

В=0=B_CЭ - B_LЭ – резонанс токов