7.3. Разложение вектора по базису. Координаты вектора Модуль вектора. Направляющие косинусы

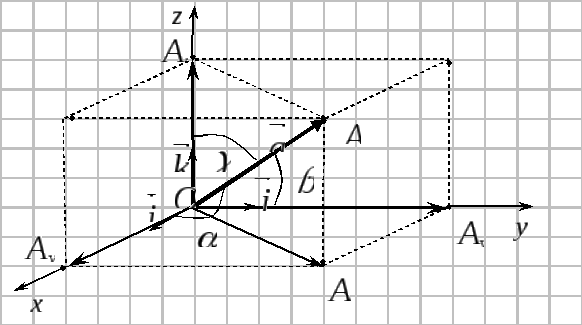
Пусть - единичные векторы осей координат, т.е. и каждый из них одинаково направлен с координатными осями. Тройка векторов называется координатным базисом.

Теорема. Любой вектор пространства можно разложить по базису , т.е. представить в виде , где - некоторые числа (буквы: - «мю», - «ню»).

Это разложение единственное.

 Доказательство. Приложим вектор к началу координат, обозначим его конец . Проведем через точку плоскости, перпендикулярные осям координат. Пусть , , - точки пересечения этих плоскостей с осями координат.

Существует единственная тройка чисел , , таких, что

.

Формула называется разложением вектора по координатному базису.

Числа , , - называются координатами вектора , т.е. координаты вектора есть его проекции на соответствующие координатные оси. В символическом виде записывают .

Например, если, то его координаты .

Зная координаты вектора , длину его можно найти по формуле

Если известны координаты точек и , то координаты вектора равны: .

Пусть углы вектора с осями , , соответственно равны , , . Числа , , называются направляющими косинусами вектора .

; ; ;

- основное свойство направляющих косинусов вектора.

7.4. Действия над векторами, заданными координатами

Пусть векторы и заданы своими координатами.

При сложении (вычитании) векторов их одноименные координаты складываются (вычитаются), т.е.

При умножении вектора на число координаты его умножаются на это число, т.е. .

Если вектор коллинеарен вектору , то можно записать , где - некоторое число, т.е. , , . Отсюда, , , или - условие коллинеарности векторов.

7.5. Деление отрезка в данном отношении

,

,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,

Пусть даны координаты точек и ; и отношение . Требуется найти координаты точки .

Из равенства векторов следует равенство соответствующих координат:

.

Аналогично, ; .

В частном случае: - середина отрезка, т.е. .

Пример. Дан треугольник , где , , .

Н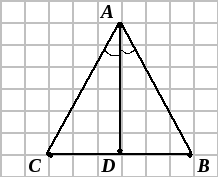айти координаты точки - пересечения биссектрисы угла со стороной .

 , ,

, .

.

;

;

Ответ: . 

§ 8. Скалярное произведение векторов

8.1. Определение скалярного произведения

Определение. Скалярным произведением вектора на вектор

называется число (скаляр), равное произведению длин этих векторов на косинус угла между ними.

Обозначается: или .

Н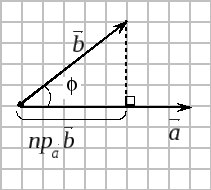айдем проекцию вектора на вектор .

Из геометрии известно .

Умножим и разделим левую часть на :

, аналогично находим .

8.2. Свойства скалярного произведения

1.

 Доказательство. . 

2. .

3. .

4. .

Определение: Число, равное , называется скалярным квадратом вектора .

5. Скалярный квадрат вектора равен квадрату его длины .

 Доказательство. .

6. Скалярное произведение базисных векторов:

, .

8.3. Вычисление скалярного произведения векторов через координаты

Теорема. Если , , то .

 Доказательство. Запишем векторы и в виде разложения по базису, т.е. и .

Тогда

По свойству скалярного произведения базисных векторов :

	.

Таким образом, . 

8.4. Приложения скалярного произведения векторов

1. Установление перпендикулярности ненулевых векторов:

.

Если , то

- условие перпендикулярности векторов.

2. Вычисление проекции вектора на вектор:

и .

3. Определение угла между векторами:

, т.е. .

4. Работа постоянной силы.

Е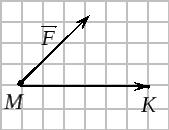сли точка перемещается прямолинейно из положения в положение под действием силы , то работа по перемещению равна:

.

Пример 1. К точке приложены три силы .

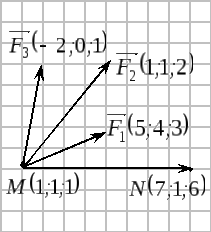Вычислить работу по перемещению точки в точку .

 - равнодействующая трех сил.

.

. 

Пример 2. Дано: , , , .

Найти угол между векторами и .

 Так как или .

,

,

Таким образом, . 

Пример 3. Найти длину вектора , если , ,.



