13.4. Общее уравнение линии второго порядка

Общее уравнение имеет вид

.

Коэффициенты , и одновременно в нуль не обращаются.

С помощью преобразования системы координат общее уравнение линии второго порядка может быть приведено к каноническому виду.

Пусть . Получим общее уравнение линии второго порядка с осями симметрии, параллельными осям координат.

Оно приводится к каноническому виду с помощью параллельного переноса осей координат. При приведении общего уравнения к каноническому виду удобно использовать метод выделения полных квадратов.

По коэффициентам уравнения можно определить вид кривой:

- если , то это уравнение окружности;

- если , то это уравнение эллипса;

- если , то это уравнение гиперболы;

- если или , то это уравнение параболы.

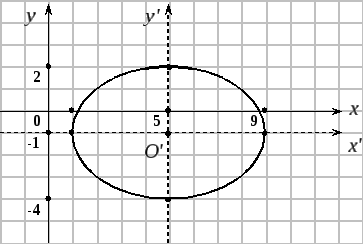
Пример 1. Привести общее уравнение к каноническому виду и построить кривую.

 По условию , уравнение эллипса. Выделим полные квадраты относительно и относительно .

- уравнение

эллипса с центром в точке и с полуосями , .

Пример 2. Привести общее уравнение

к каноническому виду и построить кривую.

 По условию , уравнение гиперболы.

В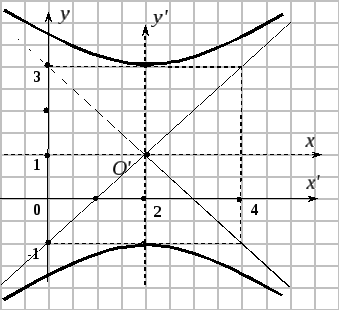ыделим полные квадраты относительно и относительно .

- уравнение гиперболы с центром в точке , действительная полуось , мнимая полуось .

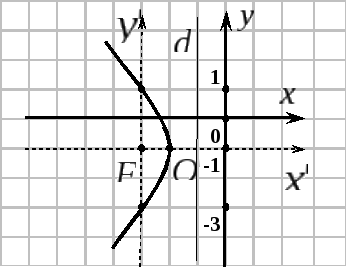
Пример 3. Привести общее уравнение к каноническому виду и построить кривую.

 По условию уравнение параболы, ось симметрии которой параллельна .

Выделим полный квадрат относительно .

- уравнение параболы с вершиной в точке , параметр , ветви направлены влево. 

Глава IV. Аналитическая геометрия в пространстве

§ 14. Плоскость

14.1. Общее уравнение плоскости

Пусть заданы: система координат , плоскость , точка и вектор . Произвольная точка принадлежит плоскости тогда и только тогда, когда векторы и будут перпендикулярны,

т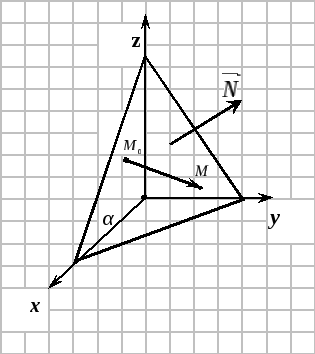.е.

Координаты векторов: ,

.

Следовательно,

(1)

- уравнение плоскости, проходящей через данную точку, перпендикулярной данному вектору,

где - текущие координаты; - координаты точки ;

- координаты вектора .

Преобразуем уравнение (1).

Получим (2) – общее уравнение плоскости .

Из общего уравнения получаем вектор , называемый нормальным вектором плоскости .

Пример. Составить уравнение плоскости, проходящей через точку перпендикулярной вектору .

 Применяя уравнение (1), получим: ;

или - это и есть общее уравнение плоскости. 

14.2. Расположение плоскости в пространстве. Уравнение плоскости в отрезках на осях.

Рассмотрим частные случаи расположения плоскости , определяемой общим уравнением: .

1. Если ,то .

, то .

Если , то .

Если , то проходит через начало координат.

2. Если , то .

Если , то .

Если , то .

3. Если , то проходит через ось .

Если , то проходит через ось .

Если , то проходит через ось .

4. Если - это уравнение плоскости .

Если - это уравнение плоскости .

Если - это уравнение плоскости .

5. Если , то уравнение плоскости можно привести к виду : или . Обозначив ,

получим (3) – уравнение плоскости в отрезках на осях,

где , , - точки пересечения с осями координат.

Примеры. Построить плоскости, заданные общими уравнениями:

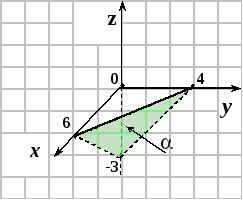
1.

.

2. .	3. .
4. .	5. .