Глава II. Элементы векторной алгебры

§ 6. Прямоугольная система координат в пространстве

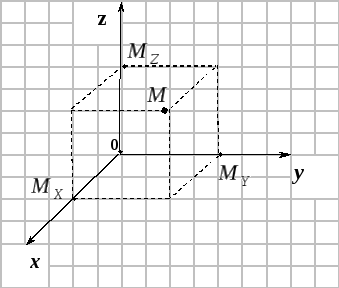Прямоугольная система координат в пространстве определяется заданием масштабной единицы измерения длин и трех взаимно перпендикулярных осей (ось абсцисс), (ось ординат), (ось аппликат), пересекающихся в одной точке , называемой началом координат.

Возьмем произвольную точку пространства и проведем через нее плоскости, перпендикулярные осям координат.

Эти плоскости пересекают оси координат соответственно в

точках: , , . Первой координатой точки , ее абсциссой, называется длина отрезка , взятая со знаком плюс, если отрезок направлен в ту же сторону, что и ось , и со знаком минус – если в противоположную. Аналогично, ординатой точки называется длина отрезка , взятая со знаком плюс или минус, аппликатой точки называется длина отрезка , взятая со знаком плюс или минус.

П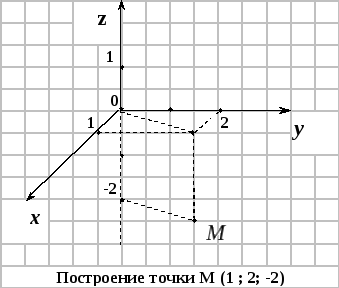ри выбранной системе координат каждой точке пространства соответствует единственная упорядоченная тройка чисел , и наоборот, каждой упорядоченной тройке чисел соответствует, и притом только одна, точка пространства.

Плоскости , , - называются координатными плоскостями. Они делят все пространство на восемь частей, называемых октантами.

Например, в первом октанте

§ 7. Векторы

7.1. Основные понятия

Вектором называется направленный прямолинейный отрезок. Если - начало вектора, а - его конец, то вектор обозначается или . Вектор называется противоположным вектору . Вектор противоположный вектору , обозначается .

Длиной или модулем вектора называется длина отрезка и обозначается . Вектор, длина которого равна нулю, называется нулевым вектором и обозначается .

Векторы и называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Обозначаются .

Векторы и называются равными , если они коллинеарны, одинаково направлены и имеют одинаковые длины.

7.2. Линейные операции над векторами

1. Умножение вектора на число. Произведением вектора на число называется вектор , который имеет длину , коллинеарен вектору , имеет направление вектора , если , и противоположное направление, если .

Например, если дан вектор , то векторы и будут иметь вид:

2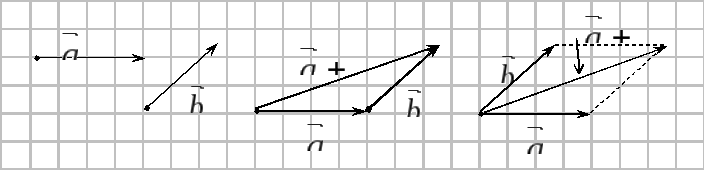. Сложение векторов. Пусть даны произвольные векторы и . Сумму векторов можно построить по правилу треугольника и по правилу параллелограмма.

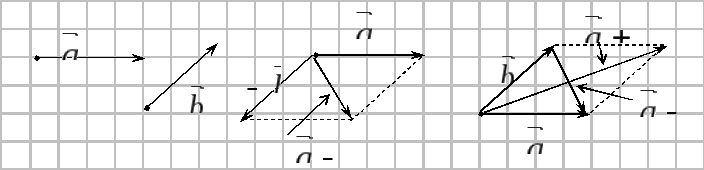
3. Вычитание векторов можно заменить сложением вектора с вектором, противоположным вектору .

4. Свойства линейных операций.

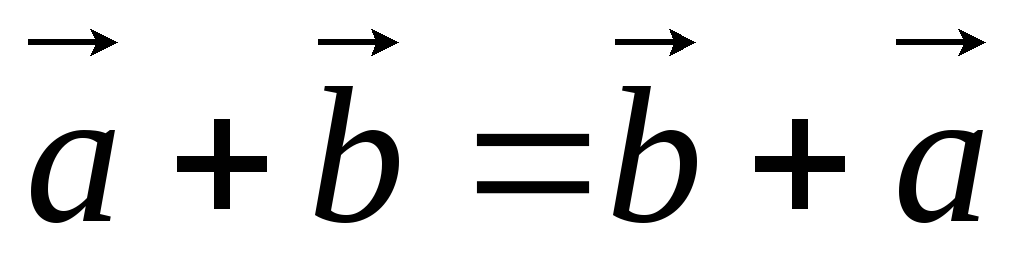
1)	- переместительное свойство сложения;
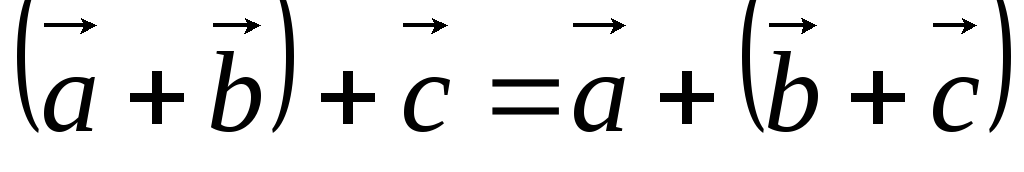
2)	- сочетательное свойство сложения;
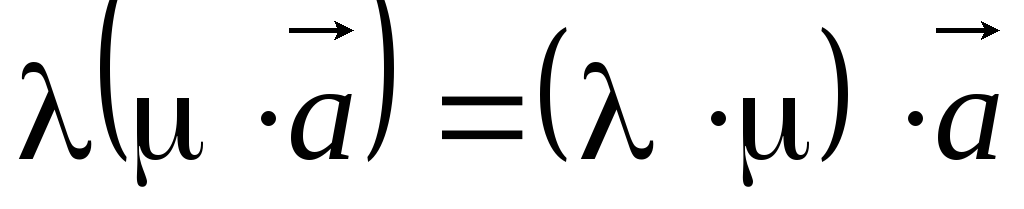
3)	- сочетательное свойство умножения на число;
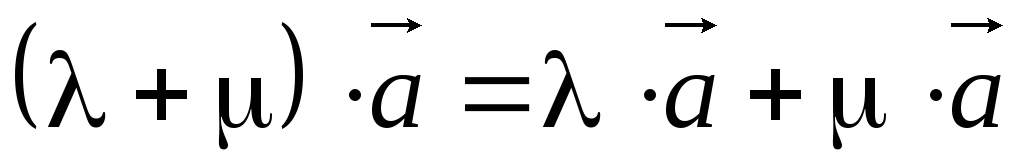
4)	- распределительное свойство относительно суммы чисел;
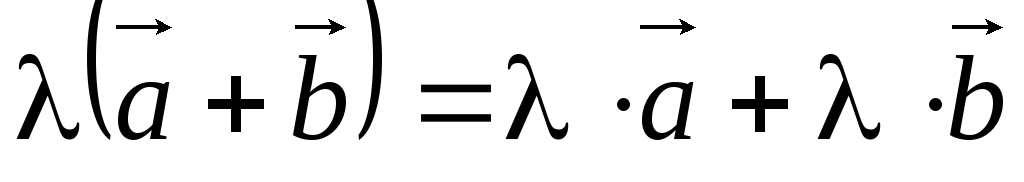
5)	- распределительное свойство относительно суммы векторов.