
- •Содержание
- •4.1. Основные понятия 10
- •5.1. Основные понятия 12
- •7.1. Основные понятия 18
- •Глава I. Элементы линейной алгебры
- •§ 1. Матрицы. Виды матриц
- •§ 2. Действия над матрицами
- •Умножение на число. Сложение и вычитание
- •Умножение матриц
- •Возведение в степень. Транспонирование матрицы
- •§3. Определители
- •3.1. Основные понятия
- •3.2. Свойства определителей
- •§4. Обратная матрица
- •4.1. Основные понятия
- •4.2. Вычисление обратной матрицы методом присоединенной матрицы.
- •4.3. Вычисление обратной матрицы методом элементарных преобразований
- •§ 5. Системы m линейных уравнений с n переменными
- •5.1. Основные понятия
- •Системы n линейных уравнений с n переменными. Формулы Крамера. Метод обратной матрицы.
- •Метод обратной матрицы
- •Метод Гаусса
- •Глава II. Элементы векторной алгебры
- •§ 6. Прямоугольная система координат в пространстве
- •§ 7. Векторы
- •7.1. Основные понятия
- •7.2. Линейные операции над векторами
- •7.3. Разложение вектора по базису. Координаты вектора Модуль вектора. Направляющие косинусы
- •7.4. Действия над векторами, заданными координатами
- •7.5. Деление отрезка в данном отношении
- •§9. Векторное произведение векторов
- •9.1. Определение и вычисление векторного произведения векторов
- •9.2. Свойства векторного произведения
- •9.3. Приложения векторного произведения
- •§ 10. Смешанное произведение векторов
- •10.1. Определение, свойства и вычисление смешанного произведения векторов
- •10.2. Приложения смешанного произведения
- •Глава III. Аналитическая геометрия на плоскости
- •§ 11. Системы координат на плоскости
- •11.1. Прямоугольная и полярная системы координат
- •11.2. Связь между прямоугольными и полярными координатами
- •11.3. Преобразование прямоугольных координат
- •§ 12. Прямая на плоскости
- •12.1. Общее уравнение прямой на плоскости
- •12.2. Частные случаи расположения прямой на плоскости. Уравнение в отрезках на осях
- •Уравнение прямой, проходящей через данную точку: а) параллельной данной прямой; б) перпендикулярной данной прямой.
- •Уравнение прямой , проходящей через две точки. Каноническое уравнение прямой. Параметрические уравнения прямой.
- •12.5. Уравнение прямой с угловым коэффициентом
- •12.6. Взаимное расположение прямых на плоскости. Расстояние от точки до прямой
- •§ 13. Линии второго порядка на плоскости
- •13.1. Эллипс
- •13.2. Гипербола
- •13.3. Парабола
- •13.4. Общее уравнение линии второго порядка
- •Глава IV. Аналитическая геометрия в пространстве
- •§ 14. Плоскость
- •14.1. Общее уравнение плоскости
- •14.2. Расположение плоскости в пространстве. Уравнение плоскости в отрезках на осях.
- •14.3. Уравнение плоскости, проходящей через три точки
- •14.4. Нормальное уравнение плоскости
- •14.5. Пучок плоскостей
- •14.6. Взаимное расположение плоскостей. Расстояние от точки до плоскости
- •§ 15. Прямая в пространстве.
- •15.1. Общие, канонические и параметрические уравнения прямой
- •15.2. Уравнения прямой, проходящей через две точки
- •15.3. Взаимное расположение прямых в пространстве. Условие принадлежности двух прямых одной плоскости.
- •§ 16. Прямая и плоскость в пространстве. Условие принадлежности прямой плоскости.
- •§ 17. Поверхности второго порядка
- •17.1. Эллипсоид.
- •Однополостный гиперболоид.
- •Двуполостный гиперболоид.
- •Эллиптический параболоид.
- •Гиперболический параболоид
- •17.6. Конус второго порядка
- •17.7. Цилиндрические поверхности
- •Литература
-
Системы n линейных уравнений с n переменными. Формулы Крамера. Метод обратной матрицы.
Системы n линейных уравнений с n переменными имеют вид:
|
|
Матрица
![]() такой системы является квадратной, и
ей соответствует определитель
такой системы является квадратной, и
ей соответствует определитель
![]() -
го порядка
-
го порядка
![]() ,
называемый главным
определителем
системы. Решение системы (2), в случае
,
называемый главным
определителем
системы. Решение системы (2), в случае
![]() ,
может быть найдено по формулам
Крамера.
,
может быть найдено по формулам
Крамера.
![]() ,
,
где
![]() - вспомогательные
определители
системы.
- вспомогательные
определители
системы.
Главный определитель системы состоит из коэффициентов при переменных, а вспомогательные составляют из главного, заменяя столбец коэффициентов (при соответствующей переменной) столбцом свободных членов.
Если
![]() ,
то система имеет единственное решение;
,
то система имеет единственное решение;
если
![]() ,
то система имеет бесконечно много
решений;
,
то система имеет бесконечно много
решений;
если
![]() и какой-либо из вспомогательных
определителей не равен нулю, то система
не имеет решений (или имеет
и какой-либо из вспомогательных
определителей не равен нулю, то система
не имеет решений (или имеет
![]() (пустое множество) решений).
(пустое множество) решений).
Метод обратной матрицы
Запишем систему (2) в матричном виде и решим матричное уравнение:
![]()
![]()
Матричное уравнение
может иметь и другой вид:
![]()
![]()
-
Метод Гаусса
Одним из наиболее универсальных методов решения алгебраических систем является метод Гаусса, состоящий в последовательном исключении переменных.
Пусть дана система уравнений:
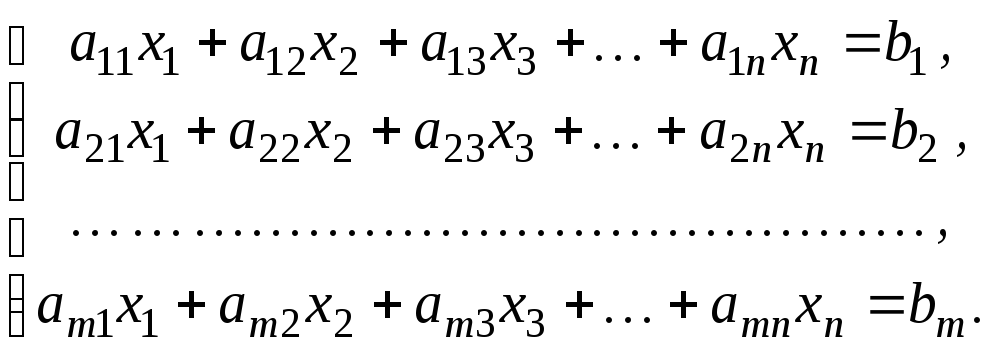
На первом этапе
(прямой ход)
систему уравнений приводим к ступенчатому
(в частном случае, когда
![]() ,
к треугольному
) виду с помощью элементарных преобразований.
,
к треугольному
) виду с помощью элементарных преобразований.
На втором этапе ( обратный ход) последовательно определяем значения переменных из полученной ступенчатой системы.
Если ступенчатая
система окажется треугольной, то
исходная система имеет единственное
решение. Из последнего уравнения находим
значение
![]() , из предпоследнего -
, из предпоследнего -
![]() ,
и далее, поднимаясь по системе вверх,
найдем значения всех остальных переменных
,
и далее, поднимаясь по системе вверх,
найдем значения всех остальных переменных
![]() .
.
Если в результате
элементарных преобразований появляются
уравнения
![]() ,
то их вычеркиваем. Если же появляется
уравнение
,
то их вычеркиваем. Если же появляется
уравнение
![]() ,
то это свидетельствует о несовместности
системы.
,
то это свидетельствует о несовместности
системы.
Преобразования Гаусса удобнее проводить не с самой системой, а с ее расширенной матрицей, выполняя элементарные преобразования над строками.
Удобно, чтобы
коэффициент
![]() был равен
был равен
![]() .
Для этого можно переставить уравнения
системы либо разделить обе части первого
уравнения на
.
Для этого можно переставить уравнения
системы либо разделить обе части первого
уравнения на
![]() .
.
Пример 1. Решить
систему уравнений методом Гаусса
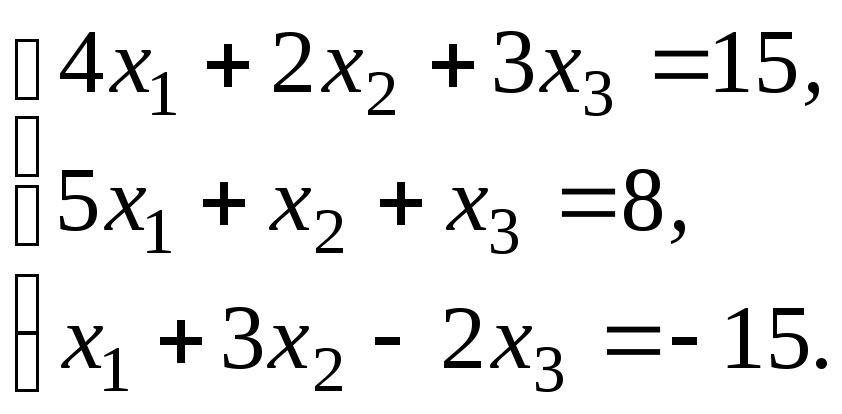
Прямой ход.
1. Выберем «ведущим» третье уравнение и запишем его на первое место.
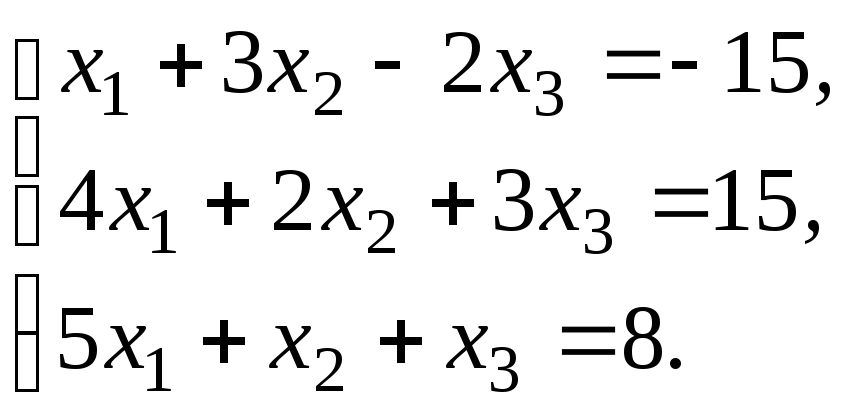
2. Запишем расширенную матрицу системы и выполним элементарные преобразования над ее строками:
|
|
|
|
первую строку перепишем, а вторую и третью заменим суммой с первой, умноженной соответственно
на
|
разделим
вторую строку на
|
|
|
|
|
первую
и вторую строки перепишем, а третью
заменим суммой ее со второй , умноженной
на
|
из этой матрицы запишем систему треугольного вида. |
Обратный ход.
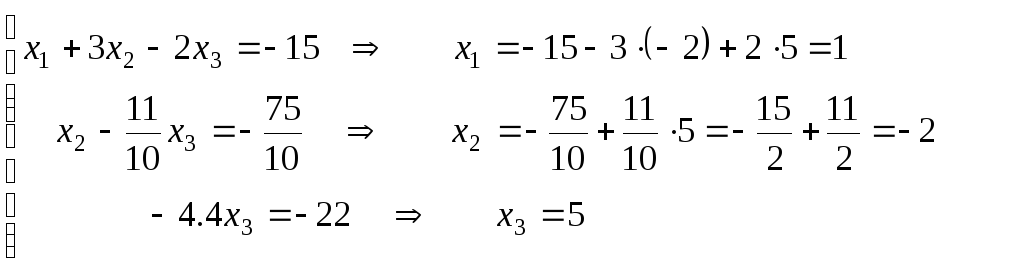
Из третьего
уравнения находим значение
![]() ,
из второго - значение
,
из второго - значение
![]() ,
из первого - значение
,
из первого - значение
![]() .
.
Ответ:
![]() .
.
Пример 2. Решить систему уравнений
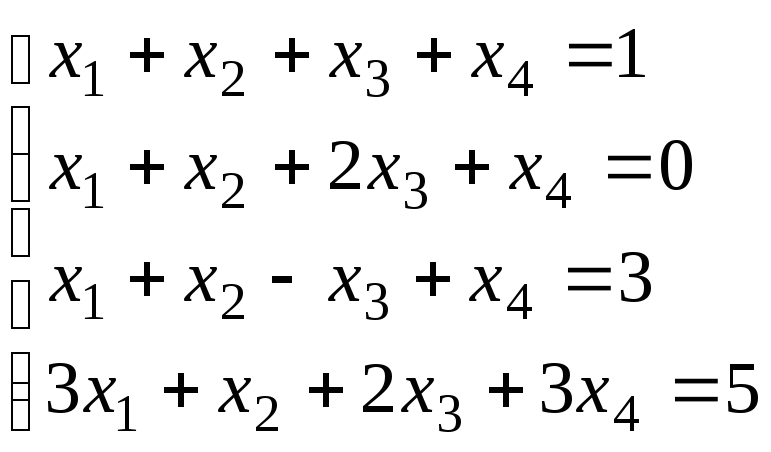
Запишем расширенную матрицу системы. Выполняя элементарные преобразования над ее строками, получим:
 ~
~
 ~
~
~
 ~
~
 .
.
Из последней матрицы запишем систему
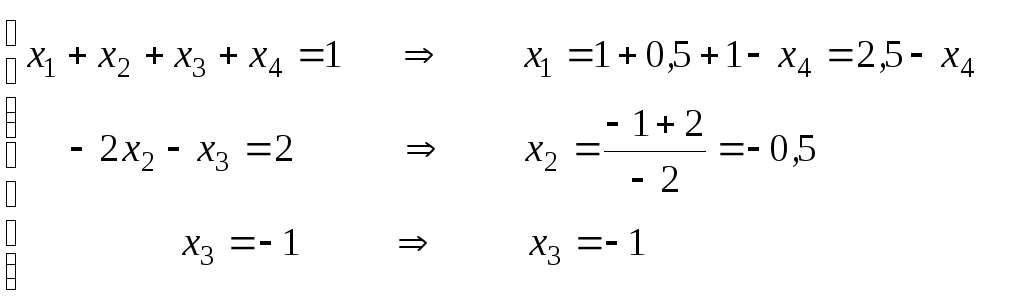
Из третьего
уравнения находим значение
![]() ,
из второго - значение
,
из второго - значение
![]() .
.
Так как уравнений
в системе осталось меньше, чем переменных,
то из первого уравнения выражаем
![]() через
через
![]() (
(![]() - свободная переменная, т.е.
- свободная переменная, т.е.
![]() -
любое число ).
-
любое число ).
Следовательно, система уравнений имеет бесконечно много решений.
Ответ:
![]() ,
где
,
где
![]() -
любое число.
-
любое число.

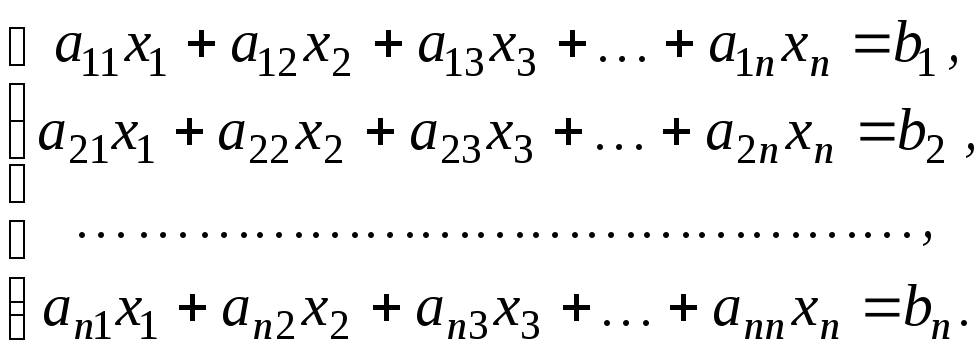 (2)
(2) ~
~ ~
~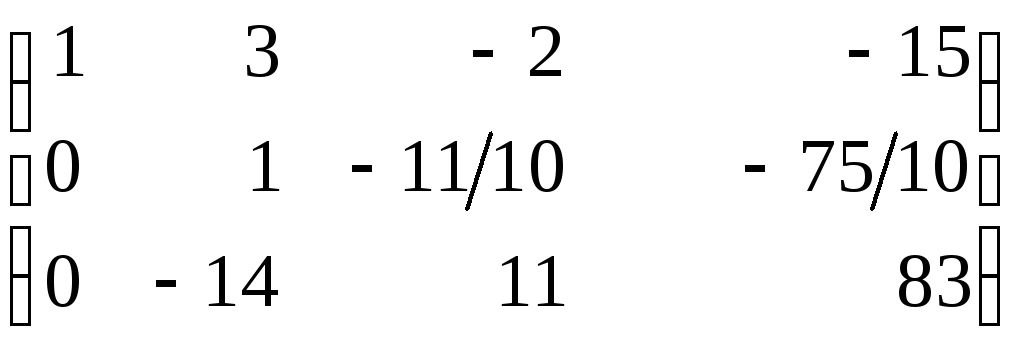 ~
~ ~
~