
- •Содержание
- •4.1. Основные понятия 10
- •5.1. Основные понятия 12
- •7.1. Основные понятия 18
- •Глава I. Элементы линейной алгебры
- •§ 1. Матрицы. Виды матриц
- •§ 2. Действия над матрицами
- •Умножение на число. Сложение и вычитание
- •Умножение матриц
- •Возведение в степень. Транспонирование матрицы
- •§3. Определители
- •3.1. Основные понятия
- •3.2. Свойства определителей
- •§4. Обратная матрица
- •4.1. Основные понятия
- •4.2. Вычисление обратной матрицы методом присоединенной матрицы.
- •4.3. Вычисление обратной матрицы методом элементарных преобразований
- •§ 5. Системы m линейных уравнений с n переменными
- •5.1. Основные понятия
- •Системы n линейных уравнений с n переменными. Формулы Крамера. Метод обратной матрицы.
- •Метод обратной матрицы
- •Метод Гаусса
- •Глава II. Элементы векторной алгебры
- •§ 6. Прямоугольная система координат в пространстве
- •§ 7. Векторы
- •7.1. Основные понятия
- •7.2. Линейные операции над векторами
- •7.3. Разложение вектора по базису. Координаты вектора Модуль вектора. Направляющие косинусы
- •7.4. Действия над векторами, заданными координатами
- •7.5. Деление отрезка в данном отношении
- •§9. Векторное произведение векторов
- •9.1. Определение и вычисление векторного произведения векторов
- •9.2. Свойства векторного произведения
- •9.3. Приложения векторного произведения
- •§ 10. Смешанное произведение векторов
- •10.1. Определение, свойства и вычисление смешанного произведения векторов
- •10.2. Приложения смешанного произведения
- •Глава III. Аналитическая геометрия на плоскости
- •§ 11. Системы координат на плоскости
- •11.1. Прямоугольная и полярная системы координат
- •11.2. Связь между прямоугольными и полярными координатами
- •11.3. Преобразование прямоугольных координат
- •§ 12. Прямая на плоскости
- •12.1. Общее уравнение прямой на плоскости
- •12.2. Частные случаи расположения прямой на плоскости. Уравнение в отрезках на осях
- •Уравнение прямой, проходящей через данную точку: а) параллельной данной прямой; б) перпендикулярной данной прямой.
- •Уравнение прямой , проходящей через две точки. Каноническое уравнение прямой. Параметрические уравнения прямой.
- •12.5. Уравнение прямой с угловым коэффициентом
- •12.6. Взаимное расположение прямых на плоскости. Расстояние от точки до прямой
- •§ 13. Линии второго порядка на плоскости
- •13.1. Эллипс
- •13.2. Гипербола
- •13.3. Парабола
- •13.4. Общее уравнение линии второго порядка
- •Глава IV. Аналитическая геометрия в пространстве
- •§ 14. Плоскость
- •14.1. Общее уравнение плоскости
- •14.2. Расположение плоскости в пространстве. Уравнение плоскости в отрезках на осях.
- •14.3. Уравнение плоскости, проходящей через три точки
- •14.4. Нормальное уравнение плоскости
- •14.5. Пучок плоскостей
- •14.6. Взаимное расположение плоскостей. Расстояние от точки до плоскости
- •§ 15. Прямая в пространстве.
- •15.1. Общие, канонические и параметрические уравнения прямой
- •15.2. Уравнения прямой, проходящей через две точки
- •15.3. Взаимное расположение прямых в пространстве. Условие принадлежности двух прямых одной плоскости.
- •§ 16. Прямая и плоскость в пространстве. Условие принадлежности прямой плоскости.
- •§ 17. Поверхности второго порядка
- •17.1. Эллипсоид.
- •Однополостный гиперболоид.
- •Двуполостный гиперболоид.
- •Эллиптический параболоид.
- •Гиперболический параболоид
- •17.6. Конус второго порядка
- •17.7. Цилиндрические поверхности
- •Литература
14.3. Уравнение плоскости, проходящей через три точки
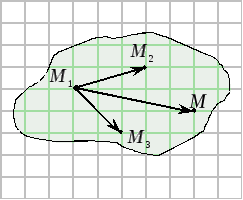
Пусть даны
точки
![]() ,
,
![]() ,
,
![]() принадлежащие плоскости
принадлежащие плоскости
![]() .
.
Точка
![]() -
произвольная точка плоскости
-
произвольная точка плоскости
![]() .
.
Построим
векторы:
![]() ,
,
![]() ,
,
![]() .
.
Так как точки лежат в одной плоскости, то векторы компланарны. Следовательно, их смешанное произведение равно нулю.
|
|
- уравнение плоскости, проходящей через три точки.
|
Пример.
Составить уравнение плоскости,
проходящей через точки
![]() ,
,
![]() ,
,
![]() .
.
Используем уравнение (4):
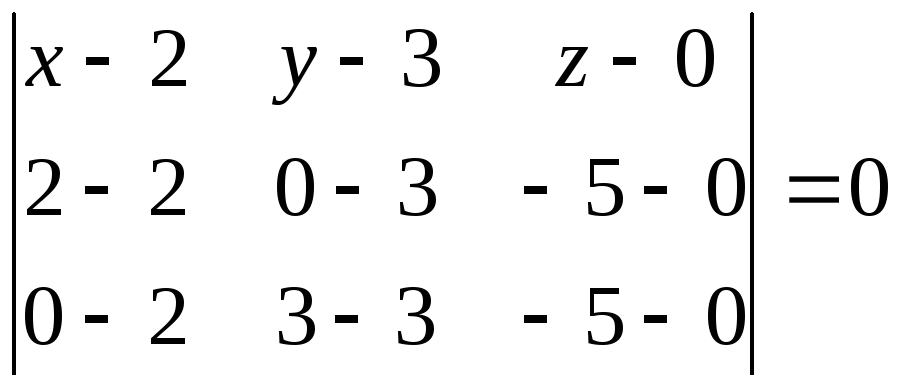
![]()
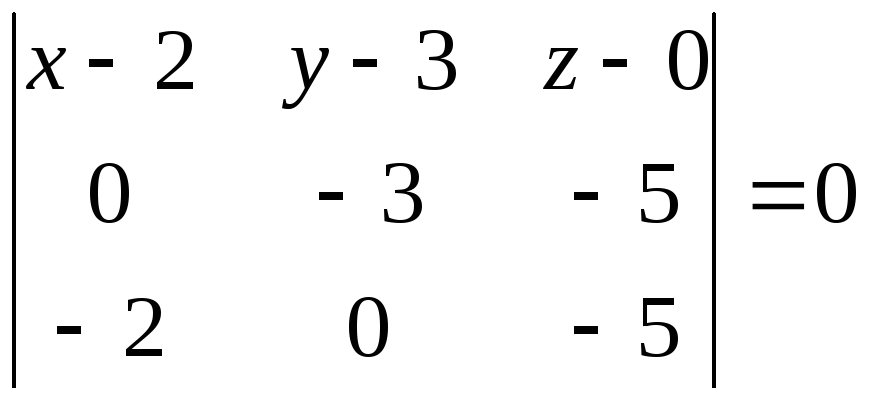
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
14.4. Нормальное уравнение плоскости
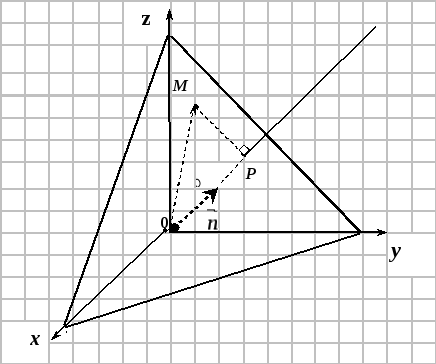 1.
Пусть в системе координат
1.
Пусть в системе координат
![]() задана плоскость
задана плоскость
![]() .
.
Проведем через
начало координат прямую, перпендикулярную
плоскости
![]() .
.
Будем называть ее нормалью.
Точку пересечения
нормали с плоскостью обозначим
![]() .
Построим вектор
.
Построим вектор
![]() ,
длину которого обозначим
,
длину которого обозначим
![]() .
.
Введем единичный
вектор
![]() ,
направление которого совпадает с
направлением вектора
,
направление которого совпадает с
направлением вектора
![]() .
.
Пусть
![]() -
углы, которые составляет вектор
-
углы, которые составляет вектор
![]() с осями координат. Так как
с осями координат. Так как
![]() ,
то
,
то
![]() .
.
2.
Выведем уравнение плоскости
![]() ,
считая известными числа
,
считая известными числа
![]() и
и
![]() .
.
Пусть
![]() -
произвольная точка. Она лежит в плоскости
-
произвольная точка. Она лежит в плоскости
![]() тогда и только тогда, когда проекция
вектора
тогда и только тогда, когда проекция
вектора
![]() на нормаль равна
на нормаль равна
![]() .
Таким образом,
.
Таким образом,
![]()
![]()
|
|
- нормальное уравнение плоскости |
3. Покажем, как привести общее уравнение плоскости к нормальному виду.
|
|
- общее уравнение. (1) |
|
|
- нормальное уравнение. (2) |
Так как
![]() то, умножая, коэффициенты уравнения (1)
на некоторый множитель
то, умножая, коэффициенты уравнения (1)
на некоторый множитель
![]() ,
получим уравнение
,
получим уравнение
![]() ,
совпадающее с уравнением (2), т. е
,
совпадающее с уравнением (2), т. е
![]() .
.
Возведем первые три из равенств в квадрат и почленно сложим:
|
|
- нормирующий множитель. |
Знак его противоположен
знаку
![]() в
общем уравнении, т. к.
в
общем уравнении, т. к.
![]() .
.
Пример.
Привести уравнение плоскости
![]() к нормальному виду.
к нормальному виду.
![]() ,
,
![]()
![]() - это и есть
нормальное уравнение плоскости
- это и есть
нормальное уравнение плоскости
![]() .
.
14.5. Пучок плоскостей
П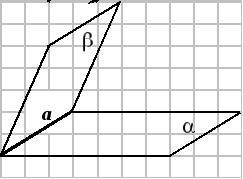 усть
плоскости
усть
плоскости
![]() и
и
![]() пересекаются по прямой a.
пересекаются по прямой a.
![]()
![]()
Определение. Плоскости, проходящие через линию пересечения двух плоскостей, образуют пучок плоскостей.
Уравнение пучка
плоскостей:
![]() .
.
Чтобы написать уравнение какой-либо плоскости пучка, достаточно знать точку, через которую она проходит.
Пример.
Написать уравнение плоскости
![]() ,
проходящей через линию пересечения
плоскостей
,
проходящей через линию пересечения
плоскостей
![]() и
и
![]() ,
и через точку
,
и через точку
![]() .
.
Запишем уравнение пучка плоскостей:
![]() .
.
Значение
![]() определяем
из условия, что плоскость проходит через
точку
определяем
из условия, что плоскость проходит через
точку
![]() :
:
![]() ,
или
,
или
![]() .
.
Следовательно, искомое уравнение имеет вид:
![]() или
или
![]() .
.
14.6. Взаимное расположение плоскостей. Расстояние от точки до плоскости
1. Пусть даны плоскости:
![]() , где
, где
![]() ,
,
![]() , где
, где
![]() .
.
-
Если
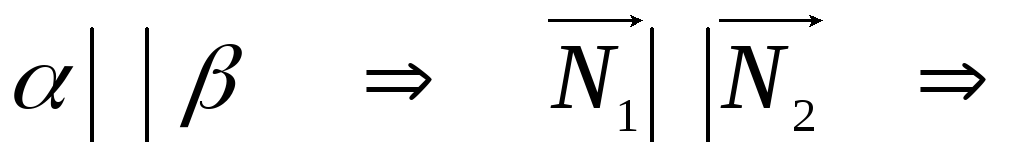
![]() - условие
параллельности
- условие
параллельности
плоскостей.
-
Если
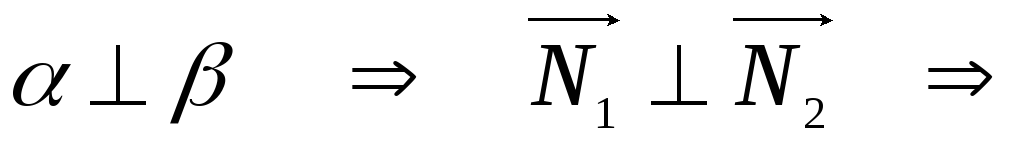
![]() - условие
- условие
перпендикулярности
плоскостей.
3. Если
![]() , то
, то
![]()
![]() -
-
2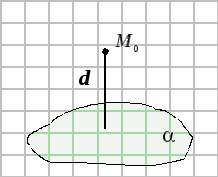 .
Расстояние от точки
.
Расстояние от точки
![]() до плоскости
до плоскости
![]()
находим по формуле:
![]()

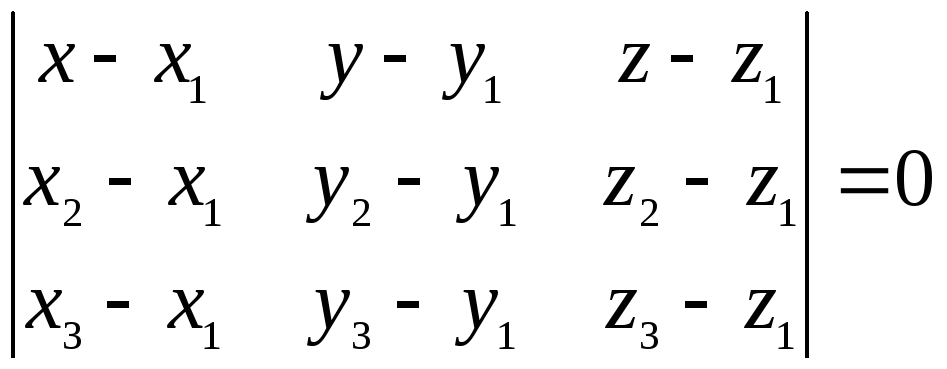 (4)
(4)