54.Друга і третя достатні умови локал. Екстр. Ф-ії.

ТЕОР.2(другі достатні умови локал. екстр.) Нехай хо стаціонарна точка ф-ії f(x) (тобто f`(xo)=0) і у деякому околі т.хо існує неперервна відміна від 0 похідна f``(x). Якщо f``(xo)<0 точка хо – точка локал. макс. ф-ії f(x). Якщо f``(xo)>0 т.хо – т. локал. мін. ф-ії f(x).

Прикл. дослідити ф-ію на екстр.

x1=1;х2=4 – стаціон. точки;

y``(x)=6x-15;

y``(1)=6*1-15=-9<0

x1=1 –точка локал. макс.

y``(4)=6*4-15=9>0;

x2=4 – т.локал. мін.

у(1)=1-7,5+12+3=8,5

у(4)=64-120+48+3=-5

Заув. порівнюючи умови теор.1 і 2 можна побачити, що теор.2 має більш вузьку обл. застосування. Цю теор. не можна застосовув. до тих точок, в яких перша похідна ф-ії не існує. Ця теор. також не дає відповіді на питання, що робити у тому випадку, коли y``(xo)=0? Однак, в останьому випадку дослідити ф-ію на екстр. іноді можливо за допомогою більш загальної теор.

Теор.3(третя достатня умова) Нехай ф-ія f(x) має неперервну похідну в околі т.хо і

а то:

1) Якщо n парне і т.хо – т. локал. макс. ф-ії f(x);

2) Якщо n парне і т.хо – т. локал. мін. ф-ії f(x);

3) якщо n непарне, то т.хо не є точкою локал. екстр.

Довед.: запиш. форм. Тейлора для ф-ії f(x): f(x)=Tn(x)+Rn(x)(1). Візьмемо у форм. (1) замість n – n-1.

Запиш. форм.(2) із залишковим членом у формі Лагранжа:

За умовою теор. з рівн.(3) одерж.

Оскільки за умовою ф-ія непер. у т.хо і то за теор. про знак непер. ф-ії існує такий окіл т.хо в якому зберігає свій знак. Будемо вважати, що форм.(4) записана для х саме з цього околу, тоді і

мають однак. знак. Розглянемо випадки:

1) якщо n парне то і Тоді з форм.(4) випливає, що

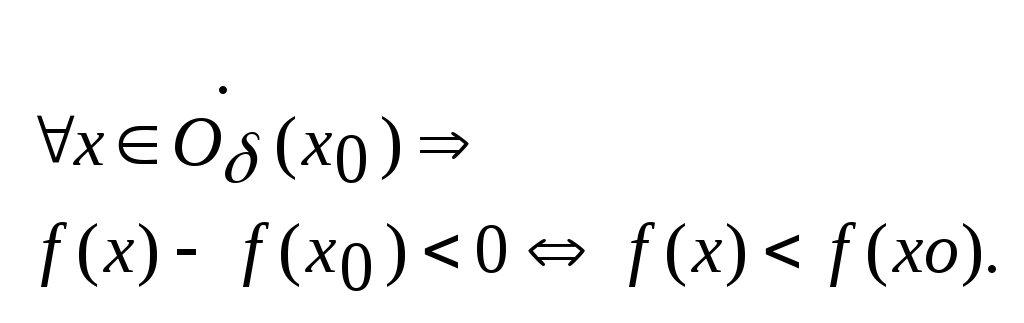
Тоді т.хо за озн. – т. локал. макс.

2) у другому випадку, коли і n парне, аналог. одерж. Тобто т.хо – т. лок. мін. ф-ії f(x).

3) коли n непарне із форм.(4) виплив., що f(x)-f(xo) на і має різні знаки. Тобто хо – не є точкою локал. екстр.

Заув. теор.2 – частиний випадок теор.3.

55.Опуклість і вгнутість кривих. Теор.1

Будемо вважати, що крива y=f(x) є гладкою на (a,b), тобто ф-ія f(x) диференц. на (a,b).

Озн.1 крива y=f(x) наз. опуклою вверх на (a,b), якщо кожна її точка, крім точки дотику, лежить нище довільної дотичної до цієї кривої.

Озн.2 крива y=f(x) наз. опуклою вниз на (a,b), якщо кожна її точка, крім точки дотику, лежить вище довільної дотичної до цієї кривої.

Заув. іноді замість термінів «опукла вверх» і «опукла вниз» вживають терміни «опукла і вгнута».

Озн.1` крива y=f(x) наз. опуклою вверх на (a,b), якщо

Озн.2` крива y=f(x) наз. опуклою вниз на (a,b), якщо

Теор.1 Нехай y=f(x) двічі дифер. на (a,b) ф-ія. Якщо крива y=f(x) опукла вверх на (a,b). Якщо крива y=f(x) опукла вниз на (a,b).

Довед. розгл. довільний відрізок [xo;x](a,b). Запиш. розкладення ф-ії y=f(x). На цьому відрізку за форм. Тейлора із залишковим членом у формі Лагранжа для n=1:

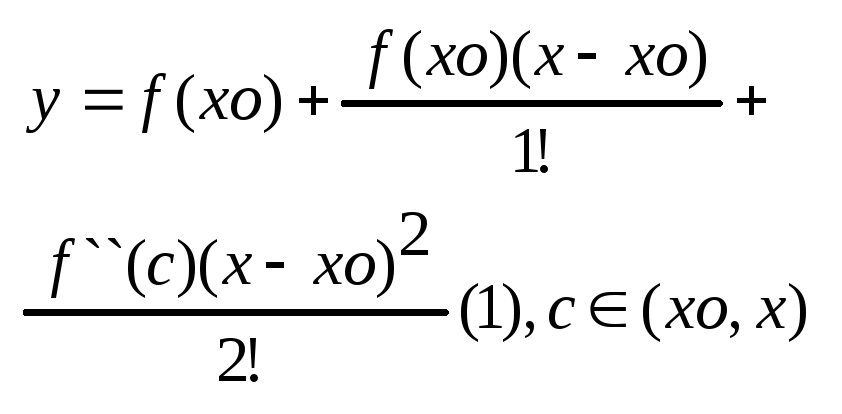
Рівн. дотичної до кривої y=f(x) у точці з абсцисою у т.хо має вигляд:

Y=f(xo)+f`(xo)(x-x0) (2).

Знайдемо різницю y-Y:

Розглянемо випадки:

1) f``(x)<0, є (a,b)

f``(c)<0 із форм.(3) одержимо, що (a,b): За озн.1` крива y=f(x) випукла вверх.

2) f``(x)>0, є (a,b)

f``(c)>0 із форм.(3)

(a,b):

За озн.2` крива y=f(x) опукла вниз на (a,b).