37.Похідна функції, заданної параметрично.

Означення

Якщо, то таке завдання функіональної залежності між змінними х та у називається параметричним завданням функції.

Припустимо, що функція диференційована на інтервалі , а функція задовольняє умові теореми про існування оберненої функції: строго монотонна . , тоді існує обернена функція , похідну якої можна знайти за формулою: . Функцію можна розглядати як складну функцію . За правилом диференційовання складної функції: . Таким чином похідна параметрично заданої функції знаходиться ха формулою: .

Приклад:

Знайти , якщо .

Лог. дифер. Похідна показн.-степен. ф-ії.

У деяких випадках доцільно спочатку прологарифмувати функцію, а лише потім знаходити її похідну. Вказана операція називається логаріфмічним диференціюванням функції. Розглянем застосування на прикладі: . Прологарифмуємо обидві частини нерівності:

Продеференцюємо по х одержану рівність:

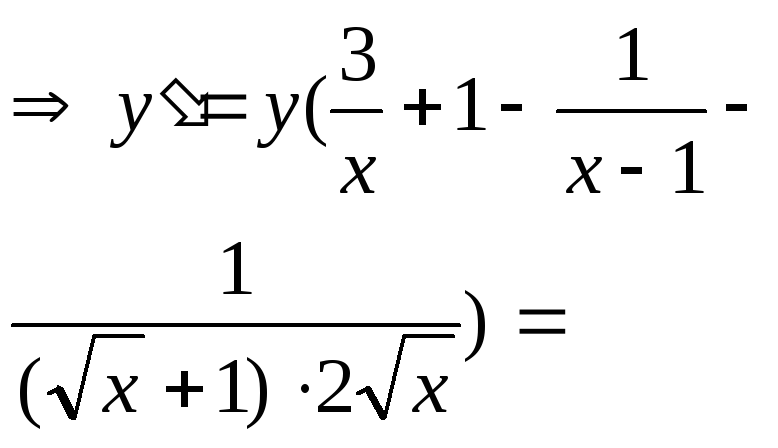
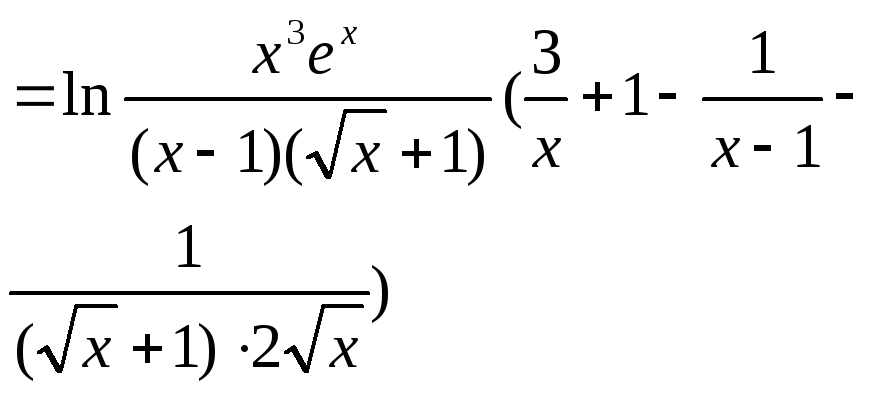
У цьому прикладі похідну функції можна було знайти двома способами за допомогою відомих правил диференціювання і логарифм. диференціюванням. Проте існують функції, похідну яких можна знайти тільки за допомогою логарифмічного диференціювання. Прикладом такої функції є показниково-ступенева функія. .

.

(1)

Приклад: .

38.Гіперболичні функції, їх властивості та похідні.

У механиці, математиці, електрониці зустрічається так звані гіперболичні функції.

Означення

Гіперболичним синусом називається функція . Функція визначена на всій числовій осі і є непарною.

Означення

Гіперболичним косинусом називається функція . Функція визначена на всій числовій прямія ося і є парною.

Означення

Гіперболичним тангенсом називається функція . Функція визначена на всійчисловій осі і є непарною.

Означення

Гіперболичним катангенсом називається функція . Функція физначена на всій числовій осі крім і є непарною.

Співвідношення, що пов’язують гіперболичні тригонометричні функції нагадують співвідношення між звичайними тригонометричними функціями.

1. 

Доведення:

2. Доведення:

а)

б)

(доказиваеться аналогично)

3. Доведення:

a)

б)

(доказіваеться аналогично)

4. Доведення:

5. Доведення:

Теорема

Похідні гіперболичних функцій знаходять за формулами:

1.

Дов:

2.

Дов:

3.

Дов:

4.

Дов:

39.Диференціал.Геом. Зміст диференц.

Диференційовність ф-ії в т.

Ф-ія f(x) диференційовна в т. х0 якщо її приріст можна записати у вигляі: у=А*х+х. (1)

де =(х)0, при х0.

А=const. Поділимо обидві частини ріняння (1) на А*х:

у~A*x. при х0, (/А)0.

А це означає що х в рівності (1) є нескінченно малою ф-ією порядку вище ніж х.

Диференціалом називається головна, лінійна відноно х чистина приросту ф-ії в т. х0.

dy=df(x)=Ax=f’(x0)x.

За диференціал незалежної змінної прицмають приріст цієї змінної.

(dx=x) Тому формула перетворю-ється на: dy=f’(x0)dx.

Критерій диференційовності ф-ії в точці.

Для того щоб ф-ія f(x) була диференційовною в т х0 необхідно і достатньо, щоб в т. х0 існувала похідна ф-ії, і іі значення було =А.

Доведення.

Н. Припустимо, що f(x)D(x0)=>

y=A*x+*x, 0, при х0.

Розділимо на х: (y/x)=A+;

Перейдемо до границі при х0

Д. Припустимо, що існує , тоді за т. про приріст ф-ії що має похідну: y=f’(x₀)*x+*x

y=A*x+*x ;

А це і означає що ф-ія є диференційовною.

Геометричний зміст диференціала

Диф. ф. в т. дорівнює приросту ординати дотичної проведеної до графіка функції в цій т.