40.Властив. Диференц.Інваріантність форми дифер.Застосув. Дифер. У наближ. Значен.

Оскільки дифер. ф-ії = добутку похідної ф-ії на диференц. незалежної змінної, то властив. дифер. аналогічні властивост. похідної:

1. dC=0, C=const

Дов. dC=C`dx=0*dx=0

2. d(Cu)=Cdu

Дов. d(Cu)=(Cu)`dx=Cu`dx=Cdu

3.

Дов.4. d(u*V)=udV+Vdu

Дов. d(uV)=(uV)`dx=(u`V+uV`)dx=

=uV`dx+Vu`dx=udV+Vdu

5.

Дов. Інваріантність форми дифер.

Нехай задана диференц. ф-ія y=f(x). За озн. її диференц. dy=y`xdx(1). Тепер будемо вважати, що х в свою чергу також є ф-єю деякої змінної Тоді визначає складну ф-ію. Її похідна а її дифер. Порівнюючи форм. (1) і (2) можна побачити, що ці форм. однакові незалежно від того чи є х незал. зміною як у форм.(1), чи є деякою ф-ією від t, як у форм. (2). Ця властив. диференц. наз. властивостю інваріантн.(незмінності) його форми і полягає в тому, що диференц. не змінює форму, незалежно від того, чи є змінна х незал., чи є деякою ф-ією.

Заст. Дифер. У наближ. Обч.

ТЕОР. якщо в т.х похідна f`(x)0, то Тобто і dy є еквівалентн. нескінчено малими.

Дов. розглян. Насл. доведена теор. дає можливість стверджувати, що при досить малих значен. виконкється наближена рівність: .

Звідси (1).

Форм. (1) застосов. в наближ. обчислен. значень ф-ії. Нехай, наприклад, . Тоді

Напр.

х=1,

За форм. (2) буде:

41. Похідні вищих порядків.

1. Нехай на відрізку [a,b] задана диференц. ф-ія y=f(x). Їїпохідна y`=f `(x) у свою чергу є також деякою ф-єю, що визначена на [a,b]. Якщо існує похідна від цієї ф-ії її наз. похідною другого порядку ф-ії f(x) і познач. симв.:

. Тобто за означ. y``(x) = (y`(x))`.

Механ. зміст другої похідної: це прискореня рухомої точки. Аналогічно, якщо існує похідна від похідної другого порядку, таку похідну наз. похідною третього порядку і т.д. Тобто: або

Прикл.: Знайти четверту похідну:

2. Нехай ф-ія задана неявно рівн. F(x,y)=0. Нагадаємо, щоб знайти першу похідну, треба продифер. по х це рівняння, вважаючи при цьому у ф-ію від х. Щоб знайти другу похідну треба продифер. по х одержаний вираз і підставити в одержане рівн. значення y` знайдене раніше.

Прикл.:

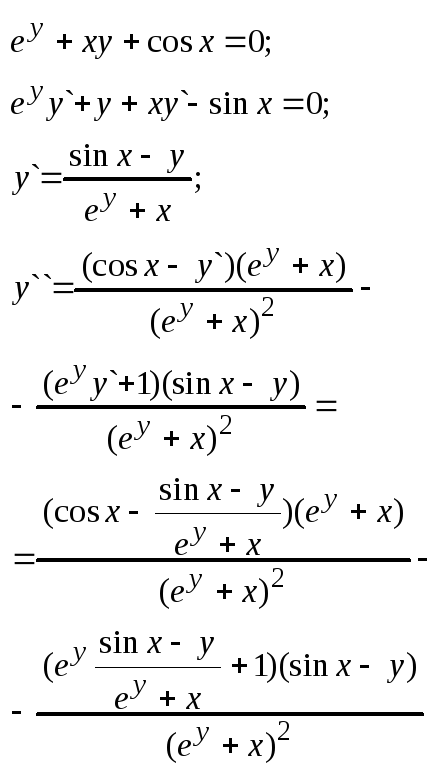
Аналог. можна знайти похідну будь-якого порядку неявно заданої ф-ії.

3. Нехай ф-ія задана параметрично рівняннями:

і крім того і ф-ія x(t) є строго монотоною. Тоді, як відомо, похідну можна знайти за формулою: Похідну другого порядку від данної ф-ії можна обчислити за правилом диференц. складної ф-ії: Розсуждаючи аналог. як у форм. (1) можна знайти похідну будь-якого порядку для параметр. заданої ф-ії (за певних умов): .

Прикл.: Знайти y``(x):

42. Форм. Лейбніца. Диференц. Вищих порядків.

Нехай y = u(x)v(x), де u = u(x) і

v = v(x) n разів диференц. ф-ії.

y`= u`v + uv`;

y``= u``v+ u`v`+ u`v` + uv`` = u``v+2u`v`+uv``. Аналогічно:

y```= u```v + 3u``v` +3u`v`` + uv```

З наведених прикладів випливає, що обчислення похідної від добутку uv конструктивно схоже з формулою . Форм., за допомогою якої, можна обчислити похідну n порядку від добутку ф-ії uv наз. форм. Лейбніца. Цю форм. можна одержати таким чином: спочатку записують розкладення за ф. бін. Ньютона , а потім замінюють показники степенів на u, а замін. на v. Ф.Лейбн. має наступний вигляд: Прикл.: Диференц. вищих порядків.

Нехай на (a,b) задана диференц. ф-ія y=f(x). Їїдифер., який наз. ще диференц. вищого порядку визначається форм.:

dy = f `(x)*dx (1).

Озн. Диференц. другого порядку (або другим дифер.) від ф-ії y=f(x) наз. дифер. від дифер. першого порядку:

Якщо зміна х незалежна, то

У форм.(2) означає не диференц. від , а добуток dx*dx. Для цього виразу ми не ставимо дужок. Аналогічно визначається диференц. n порядку У випадку, коли х незалежна зміна Слід звернути особливу увагу на те, що форм.(2) і (3) справедливі лише для випадку, коли х – незал. зміна. Виявляється, що для дифер. вищих порядків властивість інваріантності форми не викон., як це було для дифер. першого порядку. Це можна легко перевірити на прикладі дифер. другого порядку: Порівнюючи форм.(2), в якій х – незал. зміна і (4), в якій х залежить від t бачимо, що ці форм. різні. Тобто властив. інваріантн. форми не викон.