49.Форм. Тейлора з залишк. Членом у формі Лагранжа.

Познач. через Rn(x)=f(x)-Tn(x) (2).

Озн. Rn(x), що визнач. форм. (2), наз. залишк. членом ф-ії f(x), а саме поданя f(x)=Tn(x)+Rn(x) (3) наз. форм. Тейл. для ф-ії f(x) в околі т.хо. Форм.(3) таким чином можна подати у вигляді:

Якщо у форм.(4) хо=0, то одержаний вираз наз. форм. Мак Лорена розкладаня ф-ії f(x):

Заув. якщо ф-ія f(x) є деяким многочл. n степеня її залишковий член у форм. Тейл. Rn(x)=0 і ф-ія таким чином співпадає з многочл. Тейлора.

Існує декілька зображень залишкового члена Rn(x). Лагранж довів, що

а форм. Тейл.

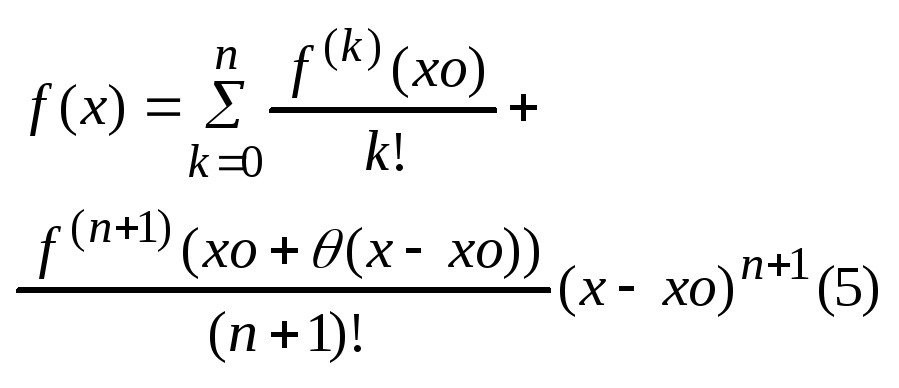
наз. форм. Тейл. із залишковим членом у формі Лагранжа. Якщо у форм.(5) хо=0, одержимо форм. Мак Лорена із залишк. член. у формі Лагранжа:

Інакше подання залишкового члена одержано Пеано. Він довів, що

50.Теор. Про умови сталості ф-ії. Наслідок.

ТЕОР. (про умови сталості ф-ії): Нехай ф-ія f(x) неперервна на [a,b] і диференц. на (a,b). Для того, щоб f(x) була сталою на [a,b] необхідно і достатньо щоб f `(x)=0, xє(a,b).

Довед. а)необхідність: нехай f(x)=c=const, xє[a,b]. Тоді f`(x)=0xє(a,b).

б)достатність: нехай f `(x) =0xє(a,b).Розглянемо т.хоє[a,b] і т.хє(a,b). На [xo,x] ф-ія f(x) задовольняє всім вимогам теор. Лагранжа. (якщо ми розглядаємо [xo,x] довед. аналогічне). Тоді f(x)-f(xo)= f`(c)*(x-xo)=0(x-xo)=0

cє(xo,x)[a,b] cє[a,b] f`(c)=0.

f(x)-f(xo)=f`(c)(x-xo)=0(x-xo)=0, де x і хо – довільні точки. Тобто f(x)=f(xo)=const. Теор. доведену

НАСЛ. Нехай ф-ії f(x) і g(x) неперервні на [a,b] диференц. на (a,b) і хє(a,b) f`(x)=g`(x). Тоді на [a,b] ф-ії f(x) і g(x) відрізняються лише на сталу.

Довед. Розглян. ф-ію (x)= f(x)-g(x). Ця ф-ія задовольняє всім вимогам попередньої теореми, оскільки xє(a,b) `(x)=f `(x)-g`(x). Тоді (х)=с або f(x)-g(x)=c або f(x)=g(x)+c.

51.Ознаки монотоності ф-ії.

ТЕОР.1(достатні умови строгої монотон.): якщо ф-ія f(x) диференц. на (a,b) і f`(x)>0 всюди на (a,b) крім можливо скінченого числа точок, в яких f `(x)=0, то ф-ія f(x) зростає на (a,b). Якщо f `(x)<0 всюди на (a,b) крім можливо скінченого числа точок, в яких f `(x)=0, то f `(x) спадає на (a,b).

Довед. розгл. випадок коли f`(x)>0(другий випадок довод. аналогічно). Візьмемо дві точки х1,х2 є(a,b) x1<x2. На (х1,х2) ф-ія f(x) задовольняє всім вимогам теор. Лагранжа. Тоді f(x2)-f(x1)=f`(c)(x2-x1). Таким чином х1,х2є(a,b): x1<x2f(x2)>f(x1). Тобто ф-ія f(x) зростаюча. Теор. довед.

Насл. Аналогічно можна довести, що у випадку коли f(x)ф-ія f(x) не спадає на (a,b), а якщо на (a,b) f`(x)0, то ф-ія не зростає на (a,b).

Теор.2(необхідні умови зростання ф-ії): Якщо ф-ія f(x) зростає на (a,b), то f`(x) 0.

Довед. протилежне не можливо, оскільки, якщо f`(x)<0 ф-ія f(x) за теор.1 спадає на інтервалі.

З теор.1і 2 випливає, що інтерв. монотоності ф-ії можуть відрізнятися один від одного точками, в яких похідна=0 або не існує.

ОЗН. точки (a,b) в яких похідна f`(x)=0 наз. стаціонарними. Стаціонарні точки, а також точки, в яких похідна не існує наз. критичними.

Схема знаходж. інтерв. монотон. ф-ії f(x):

1. Визначити область визначення ф-ії f(x);

2. Знайти похідну f`(x) і розвязати рівн. f`(x)=0;

3. Коренями даного рівн., а також точками, в яких похідна не існує, поділити обл. визначен. на проміжки, в кожному з яких визначити знак похідної. Інтервали, де f`(x)<0 – інтерв. на яких ф-ія спадає.