2. Наблюдаемость и управляемость.

Управляемость и наблюдаемость являются столь же важными свойствами объектов, как и их устойчивость. Оценка управляемости объекта должна предшествовать постановке любой задачи динамической оптимизации, ибо для не полностью управляемого объекта такая задача может оказаться неразрешимой. Оценка наблюдаемости объекта должна предшествовать постановке задачи его идентификации, ибо не полностью наблюдаемый объект не может быть идентифицирован. Для оценки управляемости и наблюдаемости обычно используются уравнение состояния и уравнение выхода объекта в их векторно-матричной форме

Принцип двойственности в тиории управляемости и наблюдаемости.

Принцип двойственности управляемости и наблюдаемости. Рассмотрим наряду с системой(I)

x = Ax + Bu; z = Hx+Lu (10.102)

так называемую двойственную ей систему(II)

х = А^Тх + H^Тu; у=В^тх+L^тх. (10.103)

система I вполне управляема по калману если сист II вполне наблюдаема по калману и система I вполне наблюдаема по калману если система II вполне управляема.

Для I

Rank[B;АВ;AB;…A^(n-1)B]=n полная управляемость

rank полная наблюдаем

для II

rank полная управляемость

Rank[B;АВ;AB;…A^(n-1)B]=n полная наблюдаем

Билет №11

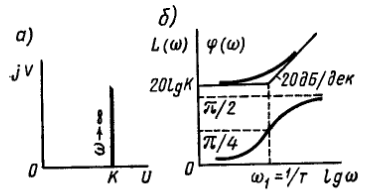
1. Элементарные типовые звенья. Дифференцирующее звено I-го порядка. Звенья, передаточные функции которых имеют вид простых множителей или простых дробей, называют типовыми или элементарными. Пропорциональное звено называют звено которое описывается уравнение y(t)=ku(t) или что то же передаточной функции W(s)=k. Интегрирующие звено называется звеном которое описывается уравнением py=ku, или передаточной функции W(s)=k/s. Дифференцирующие звено называется звено которое описывается уравнением y=kpu или передаточной функции W(s)=ks. Апериодическое звено называется звеном первого порядка, которое описывается уравнением(Tp+1)y=ku или периодически W(s)=k/(Ts+1)

Передаточная функция:

W(p)=k(Tp+1)

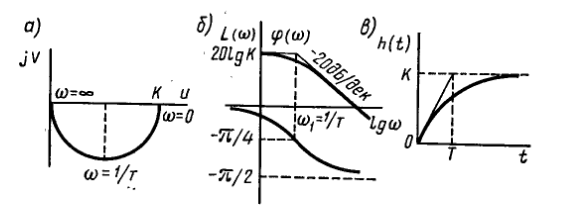
2. Наблюдаемость и управляемость. Управляемость

Под управляемостью понимают переход системы их одного состояния в другое посредством управления. Выделяют вполнеуправляемые системы и невполнеуправляемые системы.

Управляемость по Каллману

Если для производных существует управление U(t)переводящее систему за конечное время t₁-t₀. из состояния Х(t₀)=X₀ в состояние Х(t₁)=X₁, то система называется вполнеуправляемой.

Необходимое и достаточное условие имеет вид

Rank[B;АВ;A⁽²⁾B;…A^(n-1)B]=n если данное условие не выполняется то система не вполне управляема и её управляемость будет равна Rank[B;АВ;A⁽²⁾B;…A^(n-1)B]=q

q-степень управляемости. Разобъем вектор Х на 2 субвектора

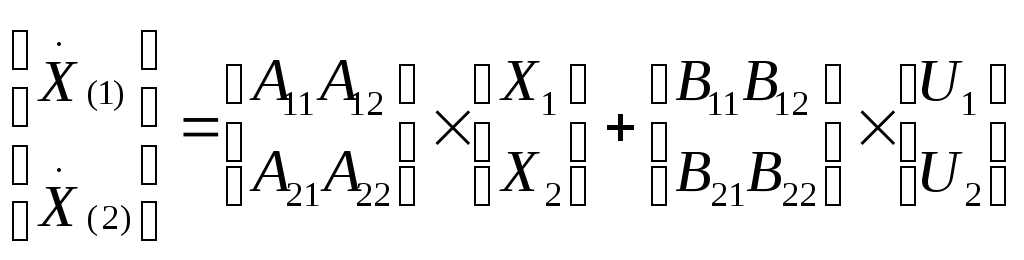если среди всех возможных разбиений на блоки

А₂₁=0 В₂₁=0 В₂₂=0 или А₁₂=0 В₁₁=0 В₁₂=0, то система вполне управляема по калману

Билет №12