2. Методы поиска оптимального решения.

1) метод Гаусса-Зайделя. В этом методе устанавливается очередность изм. Координат x1,x2,x3 и т.д. сначала делается шаг ∆x1, по первой координате знак вызванного этим шагом изменяется ∆j. Если шаг оказался неверным, то изменяют его направление и делают последующие шаги по той же координате пока ∆j не станет =0 или не изменит свой знак на противоположный, как только это произойдет делают шаг последующий координате ∆x2 и продолжают процедуру по данному принципу работает интерполятор в ЧПУ.

2 метод градиента на данном шаге изм. Производные по всем производным и следующий шаг делается одновременно по всем координатам т.о. что бы перемещение по каждой из них было пропорционально соответствующей производной тогда вектор перемещения будет направлен по градиенту при непрерывном движении по градиенту траектории движения будет нормальной к линии J равной постоянному числу. Метод градиента дает идеальный путь к экстремуму если поверхность J(x1,…xn) является сферой и параболоидом вращения.

3) метод скорейшего пуска. Сначала определяется направление градиента в начальной точке, затем осуществляется прямолинейное движение по этому направлению до тех пор пока не обратится в ноль или не изменит знак производная J=const Далее снова измеряется градиент и движение осуществляется по новому направлению. Который будет перпендикулярен предыдущему.

Система экстремума регулирования может использовать как самостоятельное, так и в состоянии с системным регулированием заданное значение координат по другому принципу. Довольно которое часто число координат определяется значение целевой функции, входят значение параметра объекта или регулятора. Тогда установка оптимальные значение представляет собой оптимальные настройки системы. Система экстремума движения автомата осуществляющую такую настройку относиться к классу самонастраеваемых систем.

Билет 6

Критерии устойчивости. Критерий Гурвица.

Устойчивость – свойство САУ возвращаться в заданный или близкий ему установившийся режим после какого-либо воздействия.

САУ устойчива, если переходные процессы в ней затухающие, выходная величина является ограниченной при условии, что входная величина также ограничена.

Критерий устойчивости Гурвица:

Пусть D(p) = a₀pⁿ + a₁p^n-1 + … + a_n, тогда:

- определитель Гурвица

Для того, чтобы система была устойчива необходимо и достаточно, чтобы ∆n и все его миноры были положительны при a₀>0.

2. Принцип максимума Понтрягина. Если (x*(t), u*(t), t*₀, t*₁) - оптимальный процесс для задачи (9)-(12), то найдутся множители Лагранжа, и (t), не равны одновременно нулю и такие , что для функционала (13) выполняется

1. Уравнения Эйлера

(14)

2. Условия трансверсальности по x:

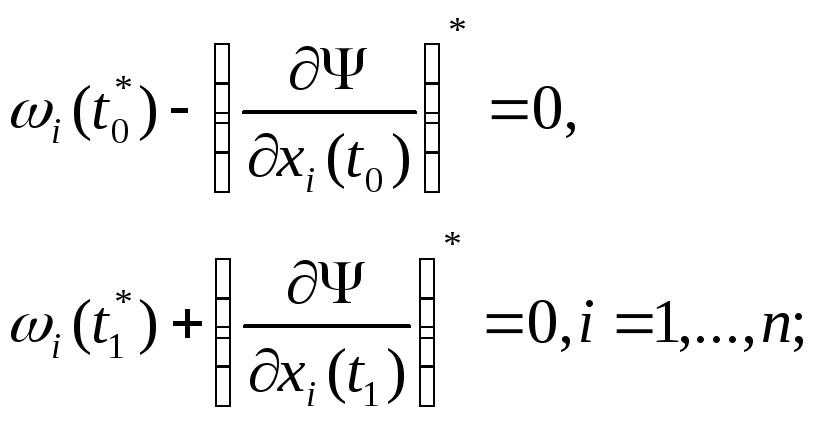(15)

3. Условия трансверсальности по t:

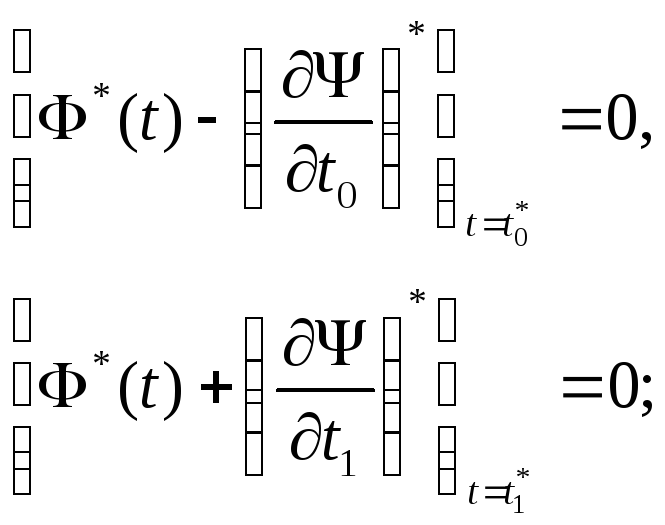(16)

4. Принцип максимума по u:

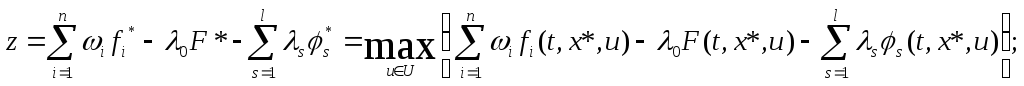
5. Условия согласованности знаков с соотношениями (10) и (11): если при некотором j в соотношении (11) (или при некотором s в (11)) стоит знак <, то соответствующее_j≥0 (_s≥0); при тех j и s, у которых в соотношениях (10) и (11) стоят знаки равенства, знаки _j и _s могут быть произвольными;

6. Условия дополняющей нежесткости:

В задачах управления встречаются два вида управления. Один из них – управление по разомкнутому контуру. В этом случае оптимальное управление определяется как функция времени {u*(t)}.

Билет 7