шпоргалка / shpory_po_teorii_avtomaticheskogo_upravleniya_tau
.docx|
1 2 1. САУ. Основные понятия и общая классификация.
Управление- это такая организация того или иного процесса, которая обеспечивает достижение определенных целей. Автоматическое Управление- это управление, осуществляемое без участия человека. Автоматическое Регулирование – поддержание постоянной или изменяющейся по некоторому заданному закону величины и суть его в измерении состояния объекта и выработки такого управляющего воздействия чтобы состояние объекта осталось в данном состоянию. Объект управления – любое регулирующееся техническое устройство или технический процесс. Общая классификация САУ: - по виду сигналов управления и типу элементов управления: линейные (непрерывные) непрерывный сигнал и линейный закон(например закон Гука); нелинейный (непрерывные), дискретные (нелинейные), цифровые (многодискретные). - по реализуемому закону управления (система автоматической стабилизации, система программного управления; следящие системы – наблюдают объект и повторяют воздействия; адаптивные системы – приспосабливаются к состоянию ОУ; самонастраивающиеся системы – меняются настройки отдельных элементов; самоорганизующиеся системы, самообучающиеся системы). - по количеству управляемых компонентов: однокоординатные и многокоординатные (независимые или зависимые каналы управления). - по принципу наблюдения: разомкнутые или с обратной связью. Обратная связь образует контур управления – одноконтурные или многоконтурные САУ.
|
3 Объект управления – любое регулирующееся техническое устройство или технический процесс. Требования к ОУ для построения САУ:
САУ описывается ДУ. Линейные системы (одноконтурные) могут быть описаны одним ДУ. Признак линейной САУ – их описание с помощью ЛДУ.
Пусть при t=0 Uвх=U0=const Uвых=U
|
5 5. Дифференциальная и операторная формы линейных ДУ.
Запись дифференциальных уравнений в операторной форме позволяет свести задачу к решению системы алгебраических уравнений. К x(t) и g(t) можно применить преобразование Лапласа.
В результате применения преобразования Лапласа можем перейти от дифференциального уравнения к алгебраическому уравнению.
После преобразования имеем следующую схему:
Уравнение САУ позволяет по x(t) найти g(t) и наоборот
Чем сложнее полином, тем сложнее система
W(p) – передаточная функция
|
6 7 6. Передаточная функция. Свойства для линейных САУ. Передаточной функцией называется отношение изображения сигнала на выходе к изображению сигнала на входе с нулевыми начальными условиями.
Свойства передаточной функции для линейных САУ: 1) Передаточная функция представляет собой дробнорациональную функцию:
Mm(p) – полином входа Dn(p) – полином выхода 2) Коэффициенты an…a0 и bm…b0 явл. Вещественными значениями и связаны физическими характеристиками системы. Для стационарной системы эти коэффициенты тоже не меняются. 3) Для реальных физических систем n ≥ m. 4) Можно составить отдельно уравнения Mm(p)=0 и Dn(p)=0, то корни уравнения этих уравнений имеют тоже некий смысл. Корни уравнения Mm(p)=0 называются нулями, а корни уравнения Dn(p)=0 полюсами. 5)Понятие свободного движения, т.е. при отсутствии входных изменений будет наблюдаться некий результат на выходе. 7. Типовые входные воздействия. Переходная функция системы. Весовая функция системы. Т.к. САУ являются сложными динамическими системами, их поведение существенно зависит от вида функции g(t). Для облегчения формализации анализа САУ, принято рассматривать их поведение при простых примитивных типовых случаях, когда задающее воздействие g(t) стандартизировано: 1)
На вход системы подаётся простейшее
единичное воздействие: На выходе наблюдается переходная характеристика h(t)
|
|||||||||||||||||||||
|
8 9 10(нач) 8. Частотные характеристики САУ.
На
вход
W(p) – передаточная ф-ия. p→j W(j W(j P( Q(
|
10(оконч) 11 2) ЛАЧХ
а)
Если
Строим график:
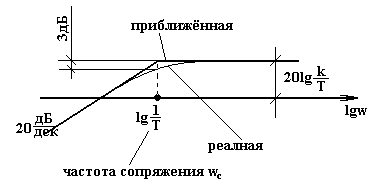
Приближённая от реальной отличаются на 3дБ. 3) ФЧХ
а)
Если
б)
если
4) АФЧХ
|
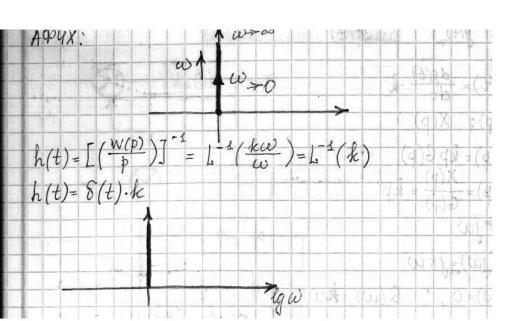
12 12. Общие свойства частотных характеристик нейтральных звеньев на примере упругого звена.
Характеристики: 1) на основании передаточной функции получим частотную функцию p→jω
ВЧХ:
МЧХ:
2) ЛАЧХ
А)
|
13 14 13. Общие принципы построения асимптотической ЛАЧХ на примере упругого звена.
L=lg(|W1W2|) = 20lg| W1|+20lg| W2|; L=20lgk+20lg| a).
w<< L=20lgk; б).
Ti→wc→1/
Ti
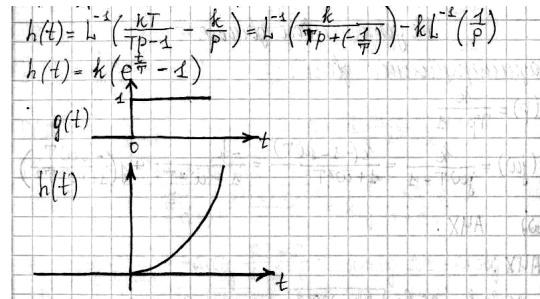
m=n – нейтральные звенья; m<n – инерционные; 14. Инерционные звенья. Идеальное интегрирующее звено. Апериодическое звено. Идеальное интегрирующее звено. Уравнение этого звена: py=kx или
в интегральной форме
Выходная величина пропорциональна интегралу от входной величины, чем и объясняется название звена. Коэффициент передачи интегрирующего звена имеет размерность 1/сек. Интегрирующее звено иногда называют астатическим. Переходная функция интегрирующего звена h(t)=kt а весовая функция w(t)=h’(t)=k Соответствующая характеристика приведены на рисунке:
|
|||||||||||||||||||||
|
2) На вход некой системы подаётся сигнал с большой амплитудой и короткий по времени(дельта воздействие):
3) Гармонический сигнал. Имеет важное значение, особенно для линейных САУ, поскольку если на входе входной сигнал гармонический, то и на выходе он тоже гармонический но с другими параметрами. К
примеру на вход
Гармонических сигнал полезен, т.к. любое входное воздействие можно разложить в ряд Фурье, следовательно выходной сигнал может быть собран из отклтков на гармоники входного. Переходная функция – выходной сигнал системы, являющийся реакцией на единичное ступенчатое входное воздействие.
Весовая функция (функция веса) – выходной сигнал САУ, в случае если входной является импульсная дельта функция.
|
|
4 4. Преобразование Лапласа. Свойства. Примеры применения. Функцией-оригиналом называется любая комплекснозначная функция f(t) вещественной переменной t, удовлетворяющая следующим условиям:
Преобразование Лапласа:
1.
Линейность
2. Теорема об дифференцировании: …
Примеры преобразований:
|
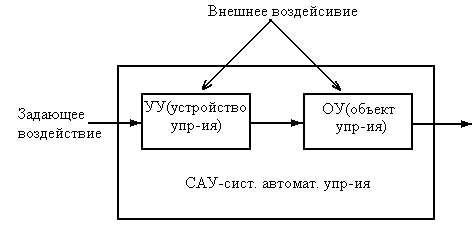
2. Сигналы в САУ и основные требования к САУ. Основные принципы управления.
Требования к САУ: - Устойчивость системы, запас устойчивости. Если САУ содержит ОС (обратную связь), то в работе таких САУ могут возникать колебания выходного параметра. Если при неизменно задаваемом воздействии отклонение от заданной величины уменьшается до 0, с течением времени, или до величины статистической ошибки, то такая система считается устойчивой. Если с течением времени отклонение возрастает (до бесконечности) , то система неустойчива. - Требования к статистическим ошибкам. Лучшими параметрами обладает статическая ошибка, но если система астатическая, то статическая ошибка должна быть минимальной. Статическая ошибка может быть положительной, отрицательной или равной 0, или стремящейся к нулю. - Требования к динамическим ошибкам. Ошибки между заданным и выходным сигналом. - Требования параметрам переходного процесса (к условиям качества). Принципы управления: - Разомкнутое. Разомкнутым системам присущи следующие недостатки: инвариантность (независимость) параметров состояния обеспечивается только по отношению к тем компонентам вектора возмущений, которые могут быть измерены; инвариантность по отношению к контролируемым (задающим) воздействиям обеспечивается только при строгом соответствии параметров объекта управления и управляющей подсистемы их расчетным значениям. - Замкнутое (включена обратная связь позволяющая контролировать наблюдаемые параметры объекта и тем самым изменять изменяющие параметры). Замкнутое управление является базовым принципом. Разомкнутое - теоретическим(т.е. имеет меньшую точность, непригодно для неустойчивых САУ, применимо для неконтролируемых ОУ)
|
|||||||||||||||||||||
|
Амплитудно-фазовая
частотная функция:
Апериодическое звено.
Переходная
функция звена определяется выражением:
|
Б)
3) ФЧХ
А)
Б)
4) АФЧХ А)
5)
А)
|
11. Методика получения передаточной функции на примере реального дифференцирующего звена.
1)
2)
3)
4)
5)
|
9. Типовые звенья САУ. Понятие минимально-фазовых звеньев. Любую сложную системы удобно анализировать условно разделяя ее на более простые компоненты(звенья) системы. Проще когда звенья имеют некие стандартные свойства и описаны типовыми уравнениями. Зная свойства звеньев и правила объединения можно манипулировать более сложными системами. Поиск звеньев может осуществляться по двум критериям: - степень простоты звена, - различия в степенях числителя и знаменателя передаточной функции.
а) m=n – нейтральное звено: пропорциональное, реальное дифф-ее звено, упругое звено. б) m>n – форсирующее звено (дифференциальные): идеальное дифференцирующее звено, форсирующее звено первого порядка. в) m<n – инерционное звено (большинство физических систем): идеальное интегрирующее звено, апериодическое звено. Понятие минимально-фазовых звеньев: Любое звено характеризуется своей передаточной характеристикой:
Приравняем
Минимально фазовыми называются звенья имеющие все нули передаточной функции в левой полуплоскости. 10. Частотные характеристики реального дифференциального звена.
p→jω
P(
Исходя из АЧХ и ФЧХ получим:
|
|||||||||||||||||||||
|
15 15. Инерционное звено 2-го порядка. Особенности частотных характеристик колебательного звена. Переходная функция колебательного звена. Инерционные звенья 2-го порядка:
T – постоянная времени. с - постоянная затухания. Если с – велико, то затухания происходят быстро. Если знаменатель уравнения прировнять к нулю, и находятся корни, то полином м.б. разложен на произведение 2-х полиномов:
Комплексность корней обеспечивает наличие колебаний. Если
с=0, то
Если на вход колебательного звена подать например гармонический сигнал. То коэффициент усиления такого звена зависит от соотношения частоты входного сигнала и собственной частоты звена. При близости этих частот происходит резонанс.
∆А- величина усиления резонанса W0- резонансная частота
|
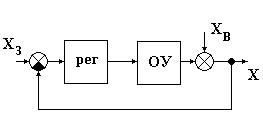
16 17 16. Соединения звеньев САУ. Обратные связи.
G(p) = L(g(t)) G1(p) = L(g1(t)) X(p) = L (x(t)) G1(p) = W2(p)X(p) (G(p)- G1(p)) W1(p) = X(p) G(p) W1(p) - W2(p) W1(p)X(p) = X(p) G(p) W1(p) = X(p) (1 + W1(p) W2(p)) W(p) = X(p)/G(p) = W1(p)/1+ W1(p) W2(p)
W(p)= M(p)/D(p) D(p)=0
D(p) + M(p) = 0
|
19
|
20
|
|||||||||||||||||||||
|
21
|
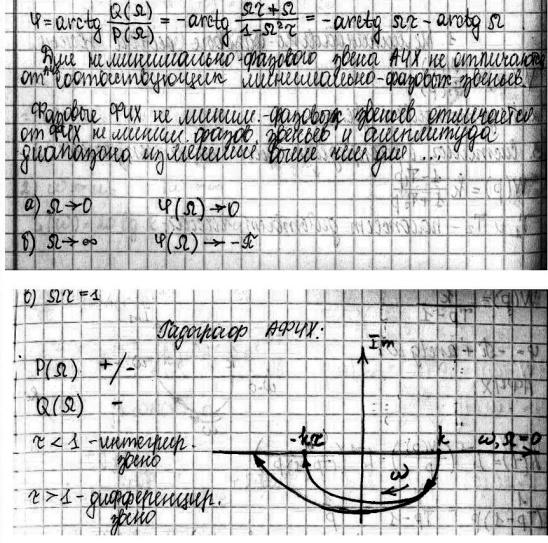
22 23 22. Особые звенья. Звено запаздывания. Трансцедентные (запаздывания) – это показат. ф-ции е в степени. Такие уравнения не явл. полиномами, но могут быть отнесены к линейным звеньям.
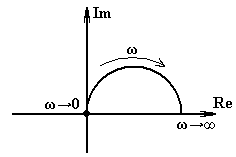
Годограф
этого звена: Бесконечное количество полюсов и нулей – немин.фазное. Трансцедент. звено наз. звеном запаздывания.
|
24 25 24. Алгебраические критерии устойчивости Гурвица и Рауса.
Определитель Гурвица имеет размерность nxn, где n – порядок хар-ого ур-ия Определитель составляется так: 1) по главной диагонали сверху вниз записывают коэф-ты а, начиная с an-1 2) Все столбцы формируют так: вниз от диагонали записывают коэф-ты по возрастанию, а вверх – по убыванию. Недостающие поля заполняются нулями. Далее формируются все главные диагональные миноры:
Формулировка критерия: Для того, что бы линейная САУ была устойчивой необходимо и достаточно что бы при an>0, определитель Гурвица, построенный по характеристическому ур-ию САУ, а также все его главные диагональные миноры были положительными. Если хотя бы 1 из них <0, то САУ неустойчива, если хотя бы 1 из них =0, то САУ нах на границе устойчивости. Если an<0, то полином нужно умножить на -1. Достоинством этого метода явл. отсутствие вычисления корней и легкость алгоритмизации. Недостаток: исследовав устойчивость разомкнутой САУ ничего нельзя сказать о замкнутой САУ; если система неустойчива то ничего неизвестно о том какой коэф-т надо поменять, что бы она стала устойчивой.
|
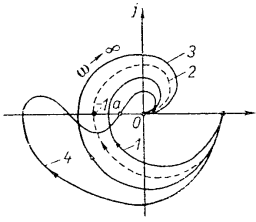
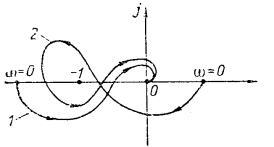
26 27 26. Критерий Найквиста. Применение для систем устойчивых в разомкнутых состояниях. Этот критерий, предложенный в 1932 г. американским ученым Г. Найквистом, позволяет судить об устойчивости замкнутой системы по амплитудно-фазовой частотной характеристике (АФЧХ) W (jω) разомкнутой системы. Когда известно, что система в разомкнутом, состоянии устойчива, условие устойчивости замкнутой системы тогда сводится к требованию, чтобы АФЧХ разомкнутой системы не охватывала точку (-1, j0). На рисунке характеристики 1 и 4 соответствуют устойчивым системам, характеристика 3 — неустойчивой, а характеристика 2 — нахождению системы на границе устойчивости. Если, например, уменьшить коэффициент передачи в неустойчивой системе, её АФЧХ сожмется к началу координат, в результате чего система станет устойчивой. Наоборот, при увеличении коэффициента передачи характеристика устойчивой системы, в конце концов охватит точку (-1, j0) и система потеряет устойчивость.
|
|||||||||||||||||||||
|
|
|
17. Форсирующие звенья САУ. Идеальное дифференцирующее звено. Форсирующее звено первого порядка. Идеальное дифференцирующее звено.
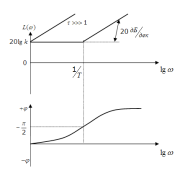
P(w)=0; Q(w)=wk; |W(jw)|=kw ЛАЧХ. L=20lg|W(jw)|=20lgk+20lgw
Форсирующее звено первого порядка. W(p) = k(τp + 1) W(jω) = k(τjω+1)
φ(ω) = arctg(τω)
|
Приближенная ЛАЧХ:
сначала
на -40 потом на +20 или наоборот, в
зависимости от того, что больше 1/Т или
Переходная функция
звена имеет вид:
α- коэффициент затухания, ω – угловая частота колебаний.
|
|||||||||||||||||||||
|
27. Критерий Найквиста. Применение для систем неустойчивых в разомкнутом состоянии. Этот критерий, предложенный в 1932 г. американским ученым Г. Найквистом, позволяет судить об устойчивости замкнутой системы по амплитудно-фазовой частотной характеристике (АФЧХ) W (jω) разомкнутой системы.
Для систем, неустойчивых в разомкнутом состоянии, критерий Найквиста имеет такую формулировку: для устойчивости системы в замкнутом состоянии АФЧХ разомкнутой системы должна охватывать точку (-1, j0). При этом число пересечений ею отрицательной действительной полуоси левее точки (-1, j0) сверху вниз должно быть на k/2 больше числа пересечений в обратном направлении, где k — число полюсов передаточной функции W (р) разомкнутой системы с положительной действительной частью. На рисунке в качестве примера показаны две АФЧХ разомкнутой системы, неустойчивой в разомкнутом состоянии вследствие наличия правых корней, но устойчивой в замкнутом состоянии. Характеристика 1 соответствует k = 1, а характеристика 2 — значению k = 2.
|
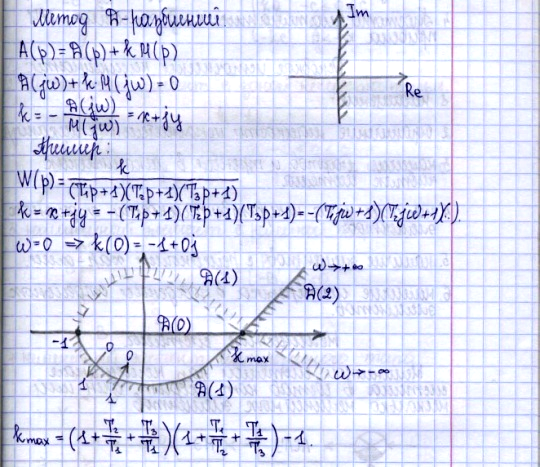
25. Частотный критерий устойчивости Михайлова. Критерий чередующихся корней. Это графический критерий. Он был предложен в 1938 г. советским учёным А.В. Михайловым, основан на рассмотрении многочлена A(p). A (p) = a0+…+anpn A(p) = an(p-p1)…(p-pn), где р1,…,pn – корни уравнения.
Подставим в этот
многочлен вместо p
мнимую переменную jω.
В результате получим комплексную
функцию:
Критерий
Михайлова формулируется так: система
устойчива, если годограф A(jω),
начинаясь на действительной положительной
полуоси, огибает против часовой стрелки
начало координат, проходя последовательно
n
квадрантов, где n-порядок
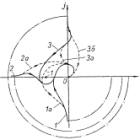
системы. На рисунке 1 годограф 1 относится к устойчивой, а годографы 3, 4 ж 5 — к неустойчивым системам. Условием нахождения системы на границе устойчивости является прохождение годографа Михайлова- через начало координат (кривая 2 на рисунке 1). Действительно, в этом случае существует значение со, при котором A(jω) = 0, т. е. характеристическое уравнение системы имеет пару сопряженных мнимых корней X = ±jω. Последнее и означает наличие в системе незатухающих колебаний, т. е. нахождение ее на границе устойчивости. При построении годографа A (jω) прежде всего находят точки его пересечения с координатными осями. Для этого, определив из уравнения ReA(ω) = 0. значения частот, соответствующих точкам пересечения годографа A(jω) с мнимой осью, подставляют их в выражение ImA (ω). В результате получают соответствующие ординаты. Аналогично находят точки пересечения A(jω) с действительной осью, приравнивая нулю мнимую часть. Критерий чередующихся корней. Данный критерий вытекает из критерия Михайлова, по сути являясь его модификацией. Можно не строить годограф, а проверить порядок пересечения осей. A (p) = a0+…+anpn A (jω) = (a0-a2w2+a4w4-…)-j(a1w-a3w3+a5w5+…) Решив ReA (ω)=0, найдем все корни ω1(pi); ImA (ω)=0, найдем все корни ω2(qi), ω(q1)=0. Формулировка: необходимым и достаточным условием устойчивости линейных САУ является то, чтобы корни вещественной части комплексной характеристической функции чередовались на числовой оси с корнями мнимой части этой функции, причем первым должен быть корень мнимой части и он должен быть равен нулю.
|
23. Устойчивость линейных САУ. Аналитический метод определения устойчивости.
Устойчивость – способность системы возвращаться в исходное состояние, если она была выведена из него под влиянием воздействия, после его прекращения. Устойчивость системы часто оценивается в разомкнутом или замкнутом состоянии. Устойчивость системы определяется по характеристическому уравнению:
Линейные САУ могут: - быть устойчивым - быть неустойчивым - находиться на границе устойчивости Необходимо различать замкнутые и разомкнутые САУ, т.к. 1. Реальные СУ исследуют в полурабочем режиме без обратной связи. 2. Если исследовать устойчивость аналитическими методами, то св-ва хар-кого уравнения ничего не скажут. 3. Некоторые частотные критерии позволяют не решать задачу дважды (исследовав св-ва разомкн. систем, можно сделать выводы о замкнутой САУ) Аналитический способ поиска корней – записывают характерное уравнение и вычисляют корни. Однако решение уравнения высокой степени сопряжено с некоторой ошибкой вычисления. Если САУ оказалось неустойчивой то из этого способа неясно как изменить параметры, что бы система стала устойчивой.
Общее
уравнение ЛДУ: Все корни должны лежать в левой полуплоскости. Достоинства метода – наглядность и математическая логичность. Другие способы не связаны с вычислением корней. Устойчивость определяется по косвенным хар-кам (напр. по частотным хар-кам). Точность этих способов зачастую выше, а найденные АФЧХ и весьма полезны для анализа других св-в САУ. Но поскольку корни не вычисляются все такие способы наз. критериями
|
|
|||||||||||||||||||||
|
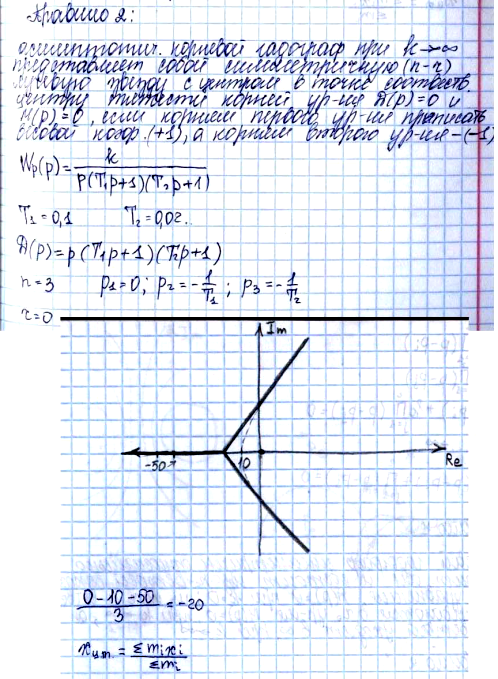
28 29 28. Критерий Найквиста. Применение для астатических систем. Этот критерий, предложенный в 1932 г. американским ученым Г. Найквистом, позволяет судить об устойчивости замкнутой системы по амплитудно-фазовой частотной характеристике (АФЧХ) W (jω) разомкнутой системы. Для суждения об устойчивости астатической системы находящееся в бесконечности начало ее АФЧХ, соответствующее ω = 0, надо мысленно соединить с положительной действительной полуосью против часовой стрелки дугой бесконечного радиуса, как условно изображено на рисунке штрих-пунктирными линиями. В случае устойчивой системы точка (—1, j0) не должна охватываться АФЧХ, мысленно дополненной дугой, соединяющей ее с положительной действительной полуосью. Сказанное иллюстрируется на рисунке.
На рисунке приведены АФЧХ астатических систем с разным порядком астатизма. Кривые 1, 2 и 3 относятся к системам соответственно с астатизмом 1, 2 и 3-го порядков. АФЧХ астатических систем при ω = 0 уходят в бесконечность, так как в знаменателе амплитудно-фазовой функции W (jω) имеется множитель (jω)r, где r — порядок астатизма. Соответственно, как показано па рисунке, при r = 1 характеристика W (jω) при ω = 0 уходит в бесконечность вдоль отрицательной мнимой полуоси, при r = 2 — вдоль отрицательной действительной полуоси, а при r = 3 — вдоль положительной мнимой полуоси. Пунктирные кривые 1а, 2а и За (3б) соответствуют неустойчивым системам с астатизмом 1, 2 и 3-го порядков. 29. Эквивалентные преобразования структурных схем. Набор типовых звеньев соединенных разными способами образует структурную схему, которая содержит элементы: 1. типовые звенья с согласным направлением передачи сигнала; 2. типовые звенья с встречным включением (звенья обратной связи); 3. сумматоры; 4. точки ветвления сигнала; Преобразования: 1. Соседние однородные элементы разрешается менять местами друг с другом:
|
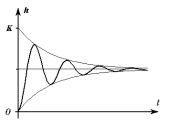
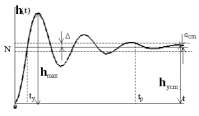
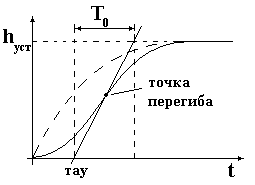
30 31 30. Качество САУ. Основные показатели. Аналитический метод определения качества. Количественные оценки качества, так называемые прямые показатели качества, определяются по кривой переходного процесса (рисунок).
Используются следующие прямые показатели качества: 1) величина перерегулирования
которая характеризует максимальное отклонение регулируемой величины от ее установившегося значения, которое может быть определено в соответствии с теоремой о конечном значении оригинала
2) время переходного процесса или время регулирования tp – наименьшее значение времени, после которого имеет место неравенство
где - заданная величина, обычно лежащая в пределах =0.02-0.05; 3) статическая ошибка сm – величина отклонения установившегося значения регулируемой величины h() от требуемого значения N
4) время установления ty – промежуток времени, по истечении которого регулируемая величина первый раз достигает установившегося значения. Для определения качества системы могут использоваться и другие показатели, соответствующие решаемой задаче, например, число колебаний регулируемой величины за время регулирования, частота и период колебаний и т.д.
|
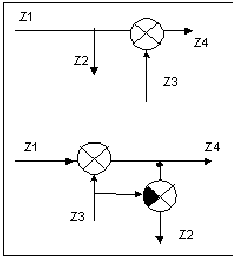
32 33 39 32. Синтез систем автоматики. Включение регулирующих устройств. Передаточные функции реальных объектов. Задача синтеза и проектирования САУ заключается в таком выборе ее структурной схемы, параметров, характеристик и способа их технической реализации, при которых требуемые динамические и эксплуатационные свойства системы обеспечиваются простыми и надежными техническими средствами. С точки зрения ТАУ целью синтеза является формирование закона управления, при котором достигаются заданные показатели устойчивости и качества системы. Закон управления – это зависимость между отклонением регулирующего органа и сигналом ошибки. Объект управления и исполнительные органы образуют, так называемую, неизменяемую часть системы, параметры которой являются исходной информацией при синтезе. Передаточную функцию неизменяемой части обозначим как W0(p). Конечная цель синтеза заключается в определении параметров специальных корректирующих устройств, которые, будучи добавлены к неизменяемой части системы, придадут ей необходимые свойства. Существуют три способа коррекции САУ. 1) Последовательная коррекция: W(p)= Wпос(p)W0(p). Wпос(p) – передаточная функция последовательного корректирующего устройства. 2) Параллельная коррекция: W(p)=Wпар(p) + W0(p). Wпарps) – передаточная функция параллельного корректирующего устройства. 3)
Коррекция в виде обратных связей: Woc(p) – передаточная функция звена корректирующей обратной связи. Разберём последовательное включение регулятора:
Передаточные функции реальных объектов:
W0(p)=ke-τp/((T0p+1)(T1p+1)m), где k=hуст, T0 – показатель инерционности объекта, τ – транспортное запаздывание.
|
34 35 36 34. Пропорциональные регуляторы. Функция ошибки. Устойчивость. Пропорциональный регулятор – это регулятор, у которого управляющее воздействие пропорционально отклонению регулируемой величины от заданного значения.
Передаточная функция по заданию равна:
Передаточная функция по возмущению равна:
Функция ошибки равна:
Критическое значение kрег, при котором система будет устойчива, равно:
|
|||||||||||||||||||||
|
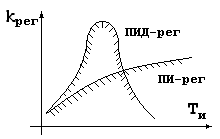
37 37. ПИД-регуляторы. Основные свойства. Устойчивость. ПИД-регулятор описывается следующим выражением:
Передаточная функция :
38 (окончание)
|
40
|
41 42
|
43
|
|||||||||||||||||||||
|
35. Интегральные регуляторы. Функция ошибки. Устойчивость. Интегральный регулятор описывается выражением:
Передаточная характеристика выглядит следующим образом: Wp(p) = kин/p Функция ошибки:
И-закон регулирования позволяет исключить статическую ошибку:
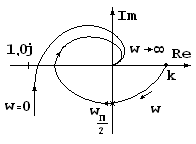
36. Пропорционально-интегральные регуляторы. Основные свойства. Устойчивость. Пропорционально-интегральный регулятор – это регулятор, у которого скорость пропорциональна отклонению и скорости изменяемой величины. Пропорционально-интегральный регулятор описывается выражением:
Передаточная функция:
Устойчивость:
|
33. Передаточная функция по возмущению. Точность и коэффициент стетизма. Имеет место следующая система:
Существует несколько различных ситуаций: 1) xB = 0. Передаточная функция по заданию:
2) xB ≠ 0. Передаточная функция по возмущению:
-x(p)wpw0+xB
Функция ошибки такой системы равна выражению: ε(p) = x3(p) – x(p), где x(p) = w3(p)x3(p) + wB(p)xB(p). Подставив это выражение, получим:
39 39. Расчёт оптимальных параметров. Последовательность действий при расчёте оптимальных параметров: 1) изучить объект управления: - получение математической модели (невысокая точность описания объектов); - экспериментальные методы (более точные, но непонятна внутренняя структура объекта). 2) Выбор показателя оптимальности системы. Чаще всего это М. 3) В пространстве параметров настроек, определить границы областей в которых система устойчива. 4) Выбрать параметры приводящие к более высокой точности.
|
31. Частотные методы анализа качества САУ. Интегральные критерии качества переходных процессов. Частотные критерии позволяют судить о качестве переходных процессов по частотным характеристикам системы. При этом могут использоваться разные частотные характеристики замкнутой системы. По АЧХ можно оценить колебательность и длительность переходной характеристики системы.
Колебательность
определяется по величине относительного
максимума характеристики, который
наывается показателем колебательности:
Длительность tn переходной характеристики определяется шириной частотной характеристики A(ω). Зависимость такая: чем шире частотная характеристика системы, тем короче её переходная характеристика, то есть тем меньше tn. Оценкой качества системы могут служить следующие интегралы:
Первый
интеграл J1
геометрически
представляет собой заштрихованную
на рисунке
площадь. (Первый переходный процесс на рисунке вызван возмущением, второй — изменением задающего воздействия.) Чем меньше эта площадь, тем предпочтительнее переходный процесс. Интегральный критерий J1 применим только к системам, о которых заведомо известно, что у них переходные процессы монотонны, то есть y(t) не меняет знака. Это резко ограничивает возможность данного критерия. Если переходный процесс колебателен, то величина J1 не может служить мерой его качества.
|
2. Перенос сумматора и типового звена:
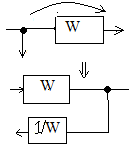
3. Перенос точки ветвления и типового звена:
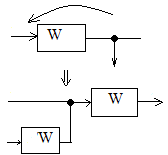
4. Перенос сумматора и точки ветвления:
|
|||||||||||||||||||||
|
|
42
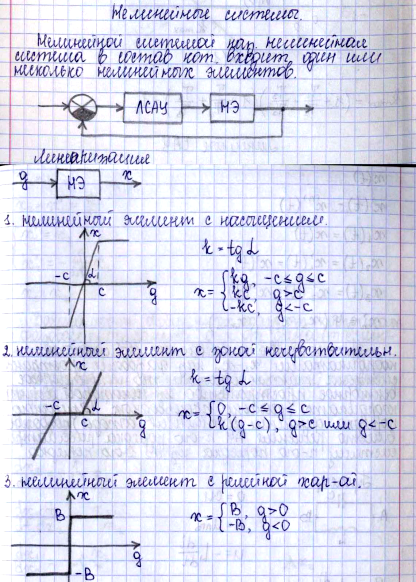
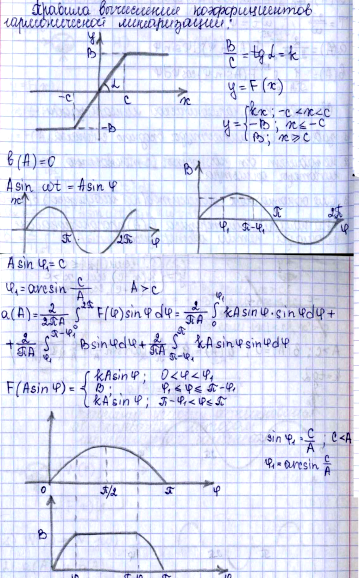
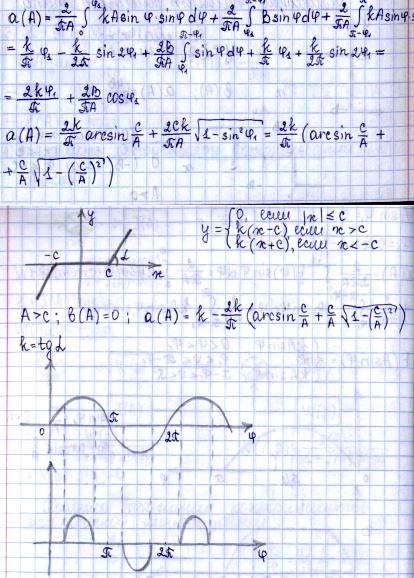
Нелинейная система – система, содержащая хотя бы одно нелинейное звено, описываемое нелинейным уравнением. Часто при наличии «небольшой» нелинейности её можно «не учитывать». Но при присутствии релейного элемента делать это нельзя. В результате описания мат. Описания нелинейности САУ составляется структурная схема, состоящая из линеариз., и нелинейных звеньев(к ним применяется метод идеализации). Нет общих методов решения нелин. Дифф. Уравнений, опис. НС. Однако комбинируя методы это возможно.(например приведение НС к типовому виду, для которых методы разработаны). НС имеют и положительные свойства: специально вводятся для получения определённых св-тв(релейные упр. устр., нелин. коррект. звенья).
|
|
38 (начало)
|
|||||||||||||||||||||
|
44
|
45
|
46
|
47
|
|||||||||||||||||||||
|
48
|
49
|
50
|
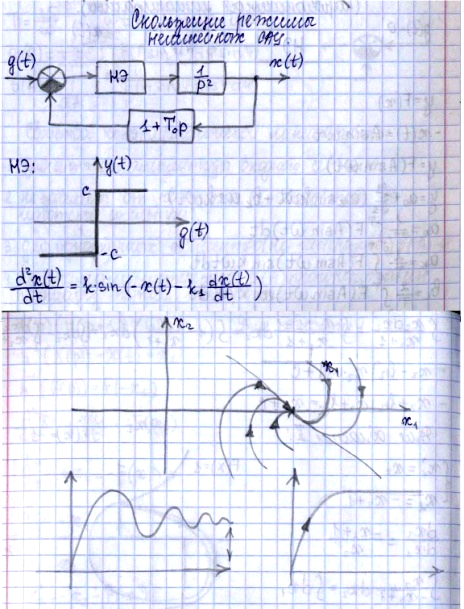
51 52 53 51. Метод Ляпунова и критерий Попова определения устойчивости нелинейных систем. Метод Ляпунова для НЭ: 1)вводятся фазовые переменные и фазовое пространство x1,x2...xn. 2)подбирается знакоопределённая ф-ия которая зависит от фазовых переменных V(x1,x2...xn)=С. 3)Ф-ия устойчива если dV/dt<0 при V>0. Знакоопределяющая ф-ия это ф-ия всезначения которой при любых x не меняет своего знака.
Критерий Попова: если линейная часть системы задана W(p) и для НЭ выполняется условие 0<=F(x)/x<=k то система устойчива, если модифицированный годограф линейной части системы находиться правее прямой проходящей через точку (-1/k;0j). Модифицированный годограф: W~(jw)=Re(W(jw))+j*w*Im(W(jw)). к – тангенс угла наклона линии охватывающая весь НЭ.
|
|||||||||||||||||||||
|
|
|
|
Фазовое пространство – пространство в прямоугольной системе координатXi, которыми явл. Величины, определяющие состояние системы. В системе n-го порядка из будет n. Для систем 2-го порядка оно двухмерное – фазовая плоскость. Каждому состоянию системы – своя точка в простр. – изображающая точка. При изменении состояния – точка перемещается – фазовая траектория. Даёт представление о системе, кроме времени(оно не рассматривается). |
|||||||||||||||||||||
|
52. Импульсные и дискретные САУ. Квантование по времени. 1)квантование по времени(КПВ) 2)квантование по уровню(КПУ) Импульсное САУ: используют КПВ
Дискретная САУ:
Недостатки: малое быстродействие. Достоин: меньшая стоимость, высокая надежность, точность, гибкость алгоритма. КПВ: аналоговый сигнал преобразует в цифровой. t – период квантования. Типы: 1)амплитудная модуляция 1-го рода 2) -//- 2-го рода(на участке t сохраняется сам сигнал) 3) Широтно-импульсное кодирование. Исходный аналоговый импульс с ∞ амплитудой это идеальный импульс или d - ф-ия: d(t-t0)= ∞(если t=t0) и =0(если t≠t0) g(t) x(t) W0(p)=X(p)/G(p)=(1-e-pT)/p т.к. G(p)=L(d(t))=1 53. Решётчатые функции. Дифференцирование и интегрирование решётчатых функций. Разностные уравнения. Решётчатая
ф-ия: f(nT)=f[n].
Для них нельзя использовать теор.
Лапласа. Первая прямая разность
∆f[n]=f[n+1]-f[n].
Первая обратная разность vf[n]=f[n]-f[n-1].
Вторая прямая разность ∆2f[n]=∆f[n+1]-∆f[n].
Вторая обратная разность
v2f[n]=∆f[n]-∆f[n-1]=f[n]-2f[n-1]-f[n-2].
Неполная сумма от n
счетов
|
|
|
|
|||||||||||||||||||||
|
54 55 56 54. Дискретное преобразование Лапласа и Z-преобразование. Вычисление Z-преобразований. Дискретное
преобразование Лапласа
Вычисление
z-преобразований:
1) по определению ф-ии наитии сумму
ряда f(t)~F(p)-L(f(t)).
Пусть F(p)
имеет простые полюса.
55. Устойчивость дискретной САУ. Билинейное преобразование. Понятие псевдочастоты. Достаточное условие устойчивости дискретных систем: P(z)=0; |zi|<1; zi=ePiT=e(αi+jβi)T=eαiT*ejβiT; где |zi|-корень ур.
Надо что бы все корни лежали в окружности от -1 до 1 если хоть один корень не удовлетворяет условию то система не устойчива. Билинейное преобразование. z1=a1+jb1; f(z1)=Re(f)+jIm(f); т.к. система дискретна то вводим что z=epT; p->jw; z=ejwT; W=(z-1)/(z+1)=(ejwT-1)/(ejwT+1)=(coswT+jsinwt-1)/(coswT+jsinwT+1)=((coswT+jsinwT-1)/(coswT+jsinwT+1))*((coswT+1-jsinwT)/(coswT+1-jsinwT))=(cos2wT-(1-jsinwT)2)/((coswT+1)2+sin2wT)=(cos2wT-1+2jsinwT-(jsinwT)2)/(cos2wt+2coswT+1+sin2wT)=(jsinwT)/(coswT+1)=(j2sin(wT/2)cos(wT/2))/(2cos(wT/2))=(jsin(wt/2))/cos(wT/2)=jtg(wT/2)=jQ; Q=tg(wT/2) – относительная псевдочастота; λ=2Q/T – абсолютная псевдочастота; w=2arctgQ/T; λ=2tg(wT/2)/T если wT<<1 то λ=w.
|
57
|
58 59
|
60
|
|||||||||||||||||||||
|
18
|
|
|
|
|||||||||||||||||||||
|
|
|
|
56. Идеальный и реальный дискретизаторы. Методика получения дискретных передаточных функций.
На схеме можно выделить как отдельный элемент импульс дискретизации. Реальный дискретизатор:
идеальный дискретизатор
Применяется следующий прием: Схема с реальным дескритизатором заменяется на схему с идеальным, и далее непрерывное звено, которое из g[n] формирует g*(t)
W(p) = L{S(t)}
После
этого
Wпнч(p)=Wнч(p)*W(p) Методика вывода дискретных передаточных функций
|
|||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||

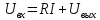
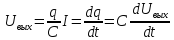
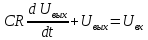 – линейное
неоднородное дифференциальное
уравнение 1-го порядка.
– линейное
неоднородное дифференциальное
уравнение 1-го порядка.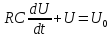
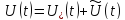
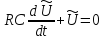
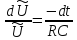
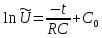
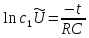
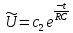
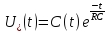
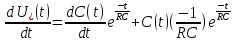
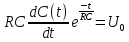
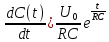
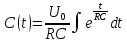
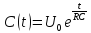


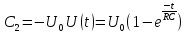
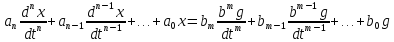
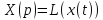

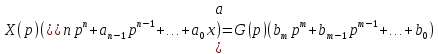
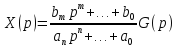
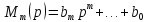 – полином входа
– полином входа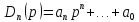 – полином выхода
– полином выхода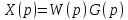
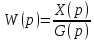
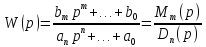
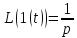
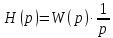
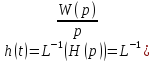 )
)
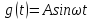
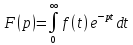 - преобразование
Лапласа
- преобразование
Лапласа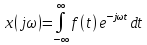 – преобразование
Фурье
– преобразование
Фурье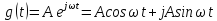 ,
то на выходе получаем тоже гармонический
сигнал, но с неким изменением амплитуды
и фазы
,
то на выходе получаем тоже гармонический
сигнал, но с неким изменением амплитуды
и фазы
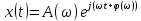

 )
– частотная функция
)
– частотная функция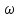 )=P(
)=P(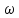 )+jQ(
)+jQ(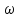 )
)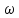 )
– ВЧХ (вещественная частотная хар-ка)
)
– ВЧХ (вещественная частотная хар-ка)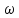 )
- МЧХ (мнимая частотная хар-ка)
)
- МЧХ (мнимая частотная хар-ка)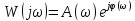
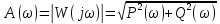 – АЧХ
(амплитудно-частотная хар-ка)
– АЧХ
(амплитудно-частотная хар-ка)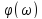 -
ФЧХ (фазовая частотная хар-ка)
-
ФЧХ (фазовая частотная хар-ка)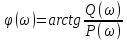
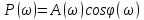
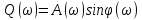
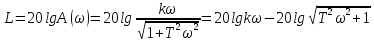
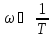 , то Tω→0
, то Tω→0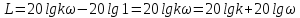 б) если
б) если
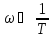 , то Tω→∞
, то Tω→∞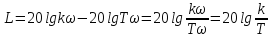
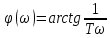

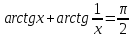
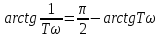
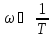 , то Tω→0
, то Tω→0
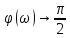
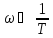 , то Tω
→ +∞
, то Tω
→ +∞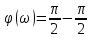


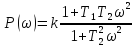
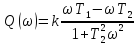
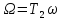
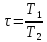
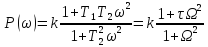
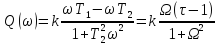
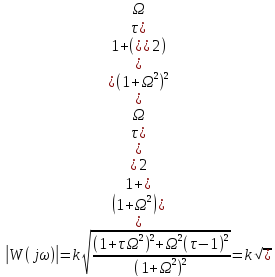
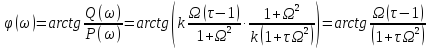
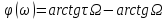
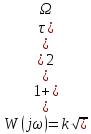
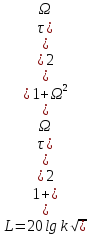
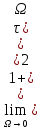
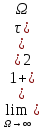
 →
→
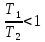 →
→
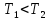
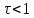 – инерционное
упругое звено или упругое интегрирующее
звено
– инерционное
упругое звено или упругое интегрирующее
звено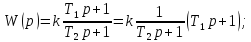
 |+20lg|
T1w+1|=20lgk+20lg
|+20lg|
T1w+1|=20lgk+20lg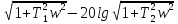 ;
;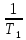 ;
w<<
;
w<< ;
;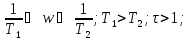

 ;
;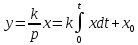
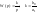 идеальное
интегрирующее звено
идеальное
интегрирующее звено
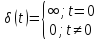
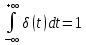
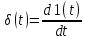
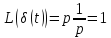
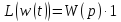
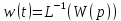
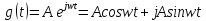 ,
то на выходе получаем тоже гармонический
сигнал, но с неким изменением амплитуды
и фазы
,
то на выходе получаем тоже гармонический
сигнал, но с неким изменением амплитуды
и фазы

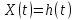
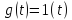
 ,
,
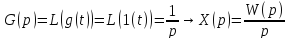
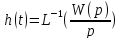
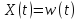
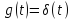
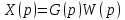 ,
,
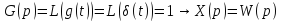
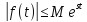
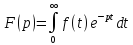
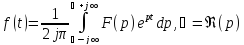
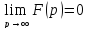
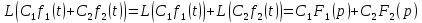
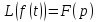
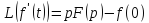
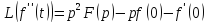
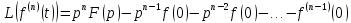

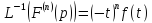
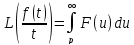
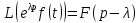
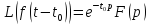
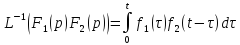
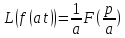
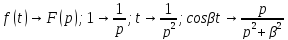
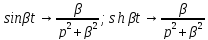
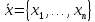 – вектор состава
объекта
– вектор состава
объекта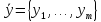 - вектор наблюдаемых
характеристик
- вектор наблюдаемых
характеристик - вектор управляющего
воздействия
- вектор управляющего
воздействия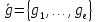 - вектор задающего
воздействия
- вектор задающего
воздействия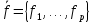 - вектор возмущающего
воздействия. Неконтролируемое внешнее
воздействие (возмущающее). Делиться
на нагрузки
– неотъемлемое внешне воздействие,
может изменяться случайным образом;
помехи
– случайные изменения в окружающей
среде.
- вектор возмущающего
воздействия. Неконтролируемое внешнее
воздействие (возмущающее). Делиться
на нагрузки
– неотъемлемое внешне воздействие,
может изменяться случайным образом;
помехи
– случайные изменения в окружающей
среде.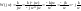
 - уменьшается с
увеличением w
- уменьшается с
увеличением w
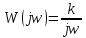
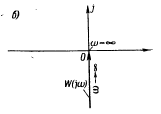

 - постоянная
времени
- постоянная
времени

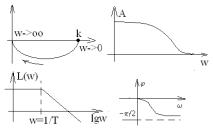
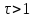 - форсирующее упругое звено или
дифференцирующее упругое звено
- форсирующее упругое звено или
дифференцирующее упругое звено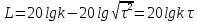

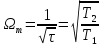
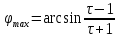
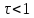

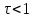 Б)
Б)
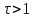
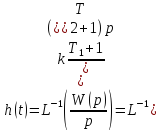
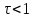 Б)
Б)
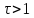
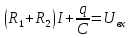
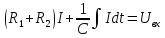

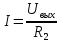



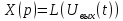
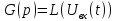
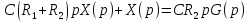
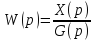
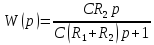
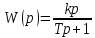 где
где
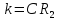 ,
,
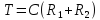

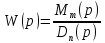
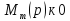 получим следующие корни уравнения
q1,
q2,
q3
... qm
получим следующие корни уравнения
q1,
q2,
q3
... qm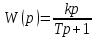 - реальное
дифференцирующее звено
- реальное
дифференцирующее звено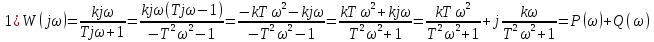
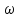 )
– ВЧХ Q(
)
– ВЧХ Q(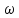 )
– МЧХ
)
– МЧХ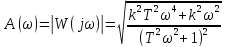 – АЧХ
(амплитудно-частотная хар-ка)
– АЧХ
(амплитудно-частотная хар-ка)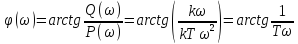 – ФЧХ
– ФЧХ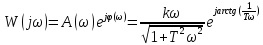
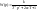 -
каноническая форма записи колебательного
звена,
-
каноническая форма записи колебательного
звена,
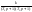 ,
а это значит, что это последовательное
соединение 2-х звеньев. Его нужно
сводить к более простым.
,
а это значит, что это последовательное
соединение 2-х звеньев. Его нужно
сводить к более простым.
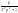 звено
является колебательным, но не затухающим,
такое звено называется
стационарным(колебательное консервативное
звено).
звено
является колебательным, но не затухающим,
такое звено называется
стационарным(колебательное консервативное
звено).
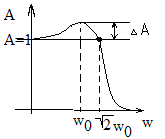
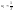 .
Система с большим затуханием препятствует
затуханию в области резонанса, но
меньше ослабляема в области больших
частот.
.
Система с большим затуханием препятствует
затуханию в области резонанса, но
меньше ослабляема в области больших
частот.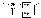
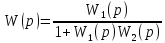 ;
;

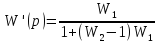 ;
;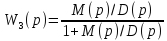 ;
;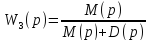 ;
;


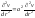 - телеграфное
уравнение Даламбера
- телеграфное
уравнение Даламбера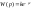 A(w)=const=k
A(w)=const=k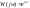

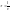
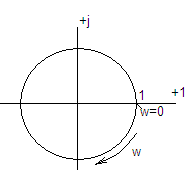
 - такое звено
будет звеном полузапаздывания или
звено замедления.
- такое звено
будет звеном полузапаздывания или
звено замедления.
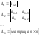
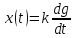 ;
; ;
;
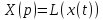 ;
; ;
;
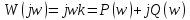 ;
;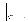
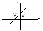
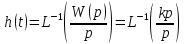 ;
; ;
;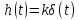 ;
;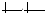

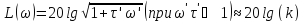
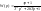 - инерционное
колебательное звено
- инерционное
колебательное звено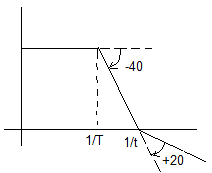
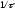
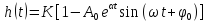
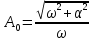 ;
;
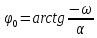 ;
;
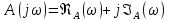 .
Изобразим A(jω)
в виде годографа в комплексной
плоскости (кривая 1 на рисунке 1). Этот
годограф называется годографом
Михайлова. Каждому значению ω
соответствуют определённые значения
ReA(ω)
и ImA(ω)
и определённая точка на плоскости.
При ω=0
функция A(jω)
= an,
то есть годограф начинается с
действительной оси. При ω
→∞ функция A(jω)
неограниченно возрастает.
.
Изобразим A(jω)
в виде годографа в комплексной
плоскости (кривая 1 на рисунке 1). Этот
годограф называется годографом
Михайлова. Каждому значению ω
соответствуют определённые значения
ReA(ω)
и ImA(ω)
и определённая точка на плоскости.
При ω=0
функция A(jω)
= an,
то есть годограф начинается с
действительной оси. При ω
→∞ функция A(jω)
неограниченно возрастает.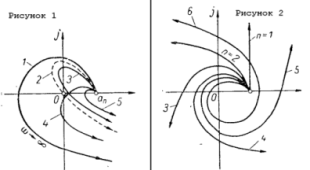
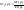 ,
в случае разомкнутого состояния
необходимо исследовать D(p)=0,
если система замкнутая, то M(p)+D(p)=0.
Корни уравнения(полюсы) разомкнутой
не совпадают с замкнутой.
,
в случае разомкнутого состояния
необходимо исследовать D(p)=0,
если система замкнутая, то M(p)+D(p)=0.
Корни уравнения(полюсы) разомкнутой
не совпадают с замкнутой.
 - корни
уравнения(полюсы)
- корни
уравнения(полюсы)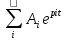 если pi<0
– убывает
если pi<0
– убывает

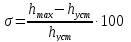 ,
,
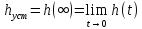 ;
;
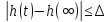
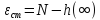
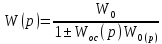 .
.
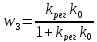 ;
;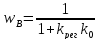 ;
;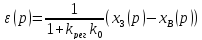 ,
где произведение k0kp
– передаточный коэффициент системы.
,
где произведение k0kp
– передаточный коэффициент системы.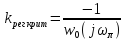 ,где
φ(ωπ)
= -π.
,где
φ(ωπ)
= -π.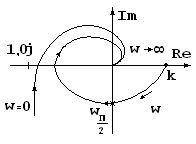
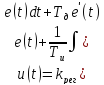 , где Тд
– время предварения регулятора.
, где Тд
– время предварения регулятора.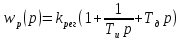
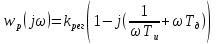

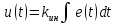 , где kин
– коэффициент передачи И-регулятора.
, где kин
– коэффициент передачи И-регулятора.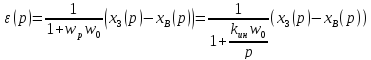

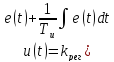 , где Ти
– время изодрома.
, где Ти
– время изодрома.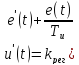
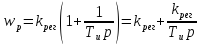

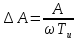 .
.
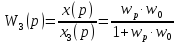 ;
;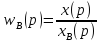 ;
; ;
;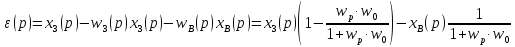 ,
отсюда
получаем:
,
отсюда
получаем: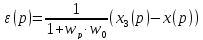 .
.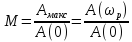 .
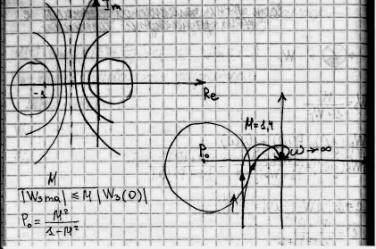
При М < 1 переходная характеристика
системы неколебательна. Оптимальным
считается M
= 1.1 .. 1.5.
.
При М < 1 переходная характеристика
системы неколебательна. Оптимальным
считается M
= 1.1 .. 1.5.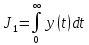 ;
;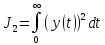 ,
где y(t)
= hуст
– h(t).
,
где y(t)
= hуст
– h(t).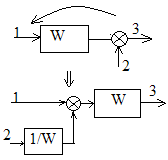









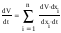


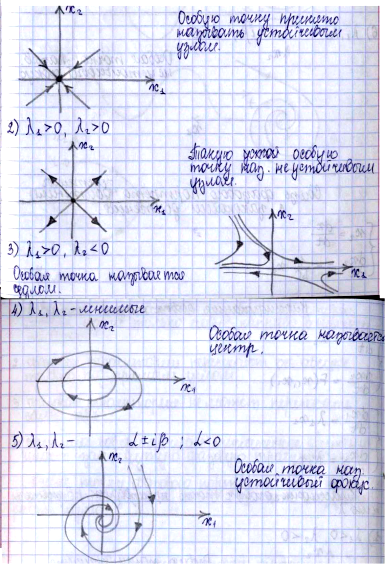

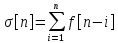 Полная сумма от n
счетов σ0[n]=σ[n]+f[n].
Разностное уравнение
f[n]=b0*vm*y[n]+b1*vm-1*y[n]+...+
bm*y[n].
Полная сумма от n
счетов σ0[n]=σ[n]+f[n].
Разностное уравнение
f[n]=b0*vm*y[n]+b1*vm-1*y[n]+...+
bm*y[n].

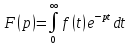 ;
;
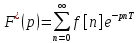 ;
epT=z;
Z
;
epT=z;
Z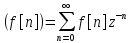 ;
1[n]=1;
;
1[n]=1;
 ;
;
 .
Таблица Z-преобразований:
.
Таблица Z-преобразований:
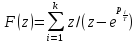 *Res(F(p));
pi=-1/T1;
W(p)=k/(T1p+1);
W(z)=z/(z-e-1/TTi)*k/T1=k/T1*(z/(z-a)),
где a=e-1/TTi
*Res(F(p));
pi=-1/T1;
W(p)=k/(T1p+1);
W(z)=z/(z-e-1/TTi)*k/T1=k/T1*(z/(z-a)),
где a=e-1/TTi






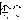
 можно
задать как
можно
задать как