1. Критерии устойчивости. Определение устойчивости по логарифмическим характеристикам

Использование ЛЧХ является частным случаем критерия Найквиста. В данном случае вводят понятие частоты среза ω_с и критической частоты ω_кр которая соответствует точке (-1;j0). ω_с- частота при которой ЛАХ пересекает нулевую ось L(ω_с)=0. ω_кр частота при которой ЛФХ пересекает ось -180⁰ φ(ω_кр)=-180⁰.

Система устойчивая в разомкнутом состоянии будет устойчива в замкнутом если ЛАХ разомкнутой системы пересекает нулевую ось раньше чем ЛФХ линию -180.

ω_с< ω_кр устойчивая

ω_с> ω_кр не устойчивая

ω_с= ω_кр на границе устойчивости

Так же учитываются правила перехода. Рассматривается переход графика ЛФХ ч/з линию -180 при положительном значении ЛАХ. При этом переход считается положительным если при увеличении частоты переход осуществляется снизу вверх в обратном случае переход является отрицательным.

2.Устойчивость сау с запаздыванием.

Существуют динамические звенья системы, у которых реакция на входное воздействие отстает по времени, на некоторую величину τ

–уравнение запаздывающего звена (звено чистого запаздывания)

Любую систему автоматического управления с запаздывающем звеном можно представить в виде соединения запаздывающего звена и линейных динамических звеньев.

τ – время чистого запаздывания

Звено чистого запаздывания может привести к потере устойчивости системы (критерий Найквиста)

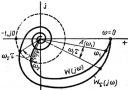
Что бы замкнутая система была устойчива нужно что бы АФЧХ разомкнутой не охватывало точку (-1,j0)

Билет 4

1. является частотным критерием и позволяет судить об устойчивости замкнутой или разомкнутой системы по виду годографа характеристического вектора соответствующей системы.

Перейдем к частотной функции характеристического многочлена, заменив p на jw:

Критерий:

Для устойчивости линейной системы n-го порядка необходимо и достаточно, чтобы годограф Михайлова при изменении частоты в интервале от 0 до ∞, начинаясь в точке на вещественной положительной полуоси последовательно обходил против часовой стрелки n квадрантов комплексной плоскости, не пересекая начало координат.

2-я формулировка:

Для устойчивости линейной системы n-го порядка необходимо и достаточно, чтобы при изменении частоты от 0 до ∞ изменение фазы частотной функции характеристического уравнения:

Свойства чередования корней.

Для устойчивости системы корни должны чередоваться.

2. Сау с запаздыванием.

это системы, имеющие в одном или нескольких звеньях запаздывание во времени начала изменения выходной величины после изменения входной на величину τ.

Уравнение динамики звена с запаздыванием можно разбить на 2:

1. Q(p)x₂=R(p)x₁*

2. x₁*(t)=x₁(t-τ)

Реальное звено с запаздыванием можно приближенно описать, используя разложение в ряд:

p – оператор дифференцирования.

W(p)=e^-τp – передаточная функция звена чистого дифференцирования.

Тогда:

Q(p)x₂ = R(p) e^-τp x_1.

Частотная передаточная функция с запаздыванием:

W(iw)=W₀(iw)e^-iwτ = A₀(w)e^i(u(w)-τw).

Билет 5

Критерии устойчивости. Критерий Найквиста.

Относится к частотным критериям и позволяет судить об устойчивости замкнутой системы по виду годографа АФХ разомкнутой системы.

Передаточная функция замкнутой системы –

Передаточная функция разомкнутой системы –

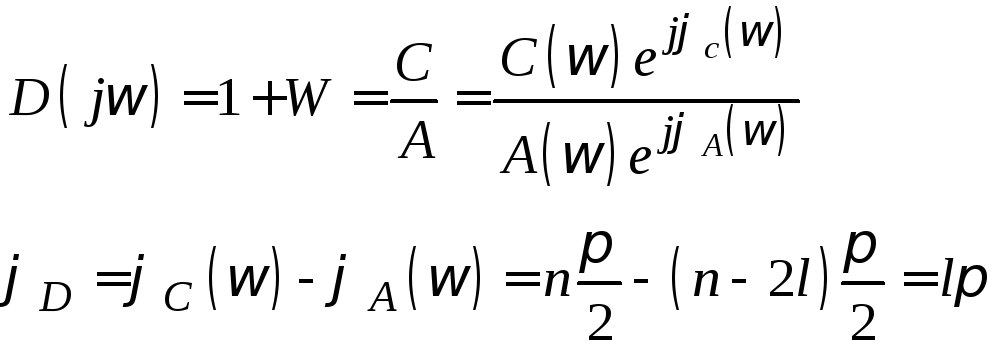
Разомкнутая система в общем случае может быть не устойчива. Но если она устойчива в замкнутом состоянии, то этого достаточно для ее работоспособности.

(-n+2l)π/2= l_*π

Для устойчивости замкнутой линейной системы n-го порядка необходимо и достаточно, чтобы при изменении частоты от 0 до ∞, изменение фазы частотной функции D(jw) равной 1+W(jw) равнялась l_*π, где l – число правых корней характеристического уравнения разомкнутой системы. Вспомогательную частотную функцию W(jw) на 1 отличающуюся от амплитудно фазовой характеристики разомкнутой системы можно рассматривать как АФХ при смещении оси ординат на -1. На практике такого смещения не делают, а рассматривают изменение фазы функции D(jw) как изменение фазы вектора, проведенного из точки с координатами (-1;j₀) к годографу АФХ разомкнутой системы. При изменении частоты до ∞ конец этого вектора скользит по годографу АФХ разомкнутой системы. Формулировка критерия:

1) Общий случай: для устойчивости замкнутой системы n-го порядка необходимо и достаточно, чтобы изменение фазы вектора проведенного из точки (-1;j₀) к годографу АФХ разомкнутой системы при изменении частоты в интервале от 0 до ∞ было равно l_*π, где l – число правых корней характеристического уравнения разомкнутой системы.

2) Частный случай 1: если в разомкнутом состоянии система устойчива, тогда для устойчивости системы необходимо и достаточно, чтобы годограф АФХ разомкнутой системы не охватывал точку (-1;j₀)

3) Частный случай 2: Особенности применения критерия Найквиста для астатических систем.

При оценке устойчивости астатических систем необходимо учитывать фазовый сдвиг определяемый левыми корнями характеристического уравнения, чтобы исключить влияние интегрирующих звеньев необходимо при w>0 достроить АФХ разомкнутой системы дугой ∞-о большого радиуса ν_*π/2 против часовой стрелки, где ν – порядок астатизма системы – число интегрирующих звеньев. Далее применяем критерий Найквиста в обычной интерпретации.